Образец выполнения ргр

Задание. Найти решение дифференциального уравнения с начальным условием на отрезке , приняв за шаг .

1. Точное решение

- линейное уравнение.

Подстановка:

При найдем

- точное решение дифференциального уравнения.

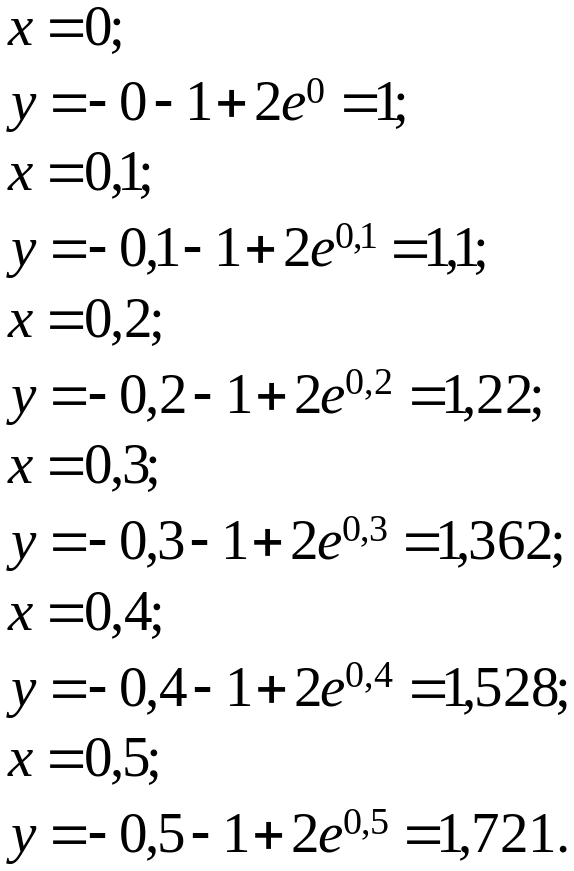
2. Приближенное решение дифференциального уравнения по методу Эйлера

Т.к. то

0
1
2
3
4
5

3. Приближенное решение дифференциального уравнения по методу Рунге-Кутта

1) Записываем в первой строке

2) Вычисляем тогда

3) Записываем во второй строке:

4) Вычисляем тогда

5) Записываем в третьей строке

6) Вычисляем тогда

7) Записываем в четвертой строке

8) Вычисляем тогда

9) В столбце записываем

10) Вычисляем

11) Получаем

Значения заносим в строку, помеченную индексом , и снова проводим вычисления по формулам (3).

Из двенадцатого столбца таблицы видно, что шаг выбран правильно.

Таблица сравнения методов Эйлера, Рунге-Кутта и точного решения уравнения.

x	Метод Эйлера	Метод Рунге-Кутта	Точное решение
	y	y	y
0	1	1	1
0,1	1,1	1,11034	1,11034
0,2	1,22	1,2428	1,2428
0,3	1,362	1,39971	1,3997
0,4	1,528	1,58364	1,58365
0,5	1,721	1,79743	1,79744

Вывод: анализируя полученные результаты, мы можем сказать, что самым точным из двух методов приближенного решения дифференциального уравнения явяляется метод Рунге-Кутта, метод Эйлера дает грубые ошибки. Метод Рунге-Кутта дает практически точное решение дифференциального уравнения, но требует большего объема вычислений, чем предыдущий метод.

Рисунок 1 – График сравнения методов Эйлера, Рунге-Кутта и точного решения дифференциального уравнения с начальным условием на отрезке и шагом .

Литература

1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. М.: «Наука», 1978. Т.2.

2. Данко П.Е., Кожевникова Т.Я. и др. «Высшая математика в упражнениях и задачах». М.: «Наука», 1980. Т.2.

3. Задачи и упражнения по математическому анализу для втузов. Под ред. Б.П. Демидовича. М.: ООО «Издательство Астрель», ООО «Издательство АСТ», 2003.

Виолетта Ивановна Тайц

Олеся Владимировна Камозина

Ирина Александровна Котова

Методические указания и задания к выполнению расчетно-графической работы по теме: «Приближенные методы решения дифференциальных уравнений»

для студентов всех направлений подготовки бакалавров очной формы обучения всех специальностей

Лицензия НД № 14185 от 6.03.2001 г.

Формат 60 94 1/16. Тираж 30 экз. Печ. л. – 1,1

Брянская государственная инженерно-технологическая академия.