2.3 Точность линейных измерений по картам

2.3.1 Реальная ошибка ( С.К.О.) положения контурной точки на карте принимается равной 0.5 мм в масштабе карты : мм, предельная мм

2.3.2 Ошибка в длине линии , измеренной по карте в раз больше ошибки определения планового положения точки.

мм,

2.3.3 Для ломаных линий : ,

где - число звеньев ломаной линии.

2. Точность определения расстояний и направлений между контурными точками плана

При подготовке исходных данных для перенесения проекта в натуру и решении других задач приходится измерять расстояния и направления между контурными точками.

4. Точность определения расстояний (горизонтальных, проложений) между близлежащими контурными точками. Съемка их про­ведена с одной точки съемочного обоснования.

Горизонтальное проложение между контурными точками: ,

где - соответственно координаты концов линий, оп­ределяемые графически.

С. к. п. линии при условии, что с.к. п. положения концов линий .

где - коэффициент автокорреляции координат контурной точки.

Коэффициент автокорреляции координат для близлежащих точек : ,

где и и соответственно с.к.п. положе­ния исходного пункта и контурной точки.

Для близлежащих контурных точек можно принять = 0,4 -0,6.

Погрешность расстояния равна погреш­ности положения контурной точки лишь при = 0. Корреляцией координат контурных точек можно пренебречь, если концы линии находятся на значительном рас­стоянии друг от друга или их съемка выполнена с разных точек съемочной сети.

Таким образом, при некоррелированных координатах, (когда = 0 ) :

Пример 1

При съемке застроенных территорий с капитальной застройкой 0,3 мм на плане . При = 0,6, для близлежащих контурных точек получим:

на плане.

С вероятностью, близкой к 1.0 предельная погрешность расстояния между близлежащими точками капитальных зданий и сооружений не превысит 0,4 мм на плане.

Пример 2

Для плана на незастроенной территории с чет­кими очертаниями контуров, погрешность т_г = 0,5мм на плане; положение точек независимо, так как их съемка вы­полнена с разных точек съемочного обоснования тогда мм на плане.Следовательно, предельная погрешность расстояния мм на плане.

3. Средняя квадратическая погрешность определения направления (дирекционного угла)

3.1 Дирекционный угол линии между точками с координатами , определяется по формуле : .

СКП определения величины дирекционного угла линии длиной S между контурными точками, положение которых некоррелировано, определится по формуле

Для близлежащих контурных точек СКП дирекционного угла:

Формулы (1.1), (1.2) показывают, что СКП дирекционного угла уменьшается с увеличе­нием расстояния между точками. Поэтому при привязке проек­та автомобильной дороги к пунктам геодезического обоснования за исходное направление принимают имеющее большую длину.

Например, при 8 см на плане и мм на плане, найдем

Предельная погрешность определения дирекционного угла

3.2 СКП измерения дирекционного угла линии длиной S между контурными точками, положение которых некоррелировано, определится по формуле

4. Точность определения высотных параметров НА плане.

Точность топографических планов в высотном отношении характеризует­ся средней квадратической или средней погрешностью определения по горизонталям плана высот точек относительно ближайших пунктов съе­мочного обоснования. Погрешности и связаны следующей зависимо­стью: = 1,25 , что следует учитывать при расчетах точности крупномасштабных топографи­ческих съемок.

Основным видом наземных топографических съемок является тахеометрическая , обладающая рядом несомненных преимуществ.

Тахеометрическая съемка про­изводятся путем набора пикетов, интерполирования и проведения горизонта­лей. Полнота и детальность изображения рельефа зависят от высоты сечения, густоты пикетов и пр. Но до мельчайших подробностей рельеф изобразить нельзя, какой бы ни была высота сечения рельефа,. Это не позволит сделать масштаб плана. При съемках приходится обобщать рельеф, выделяя главное и отбрасывая второстепенное.

Погрешности, влияющие на точность положения горизонталей:.

Первая группа - погрешности, влияющие на точность положе­ния горизонтали по высоте и не зависящие от угла наклона топографической поверхности:

1) построения съемочного обосно­вания;

2) «топографической шероховатости» поверхности земли (мелкие не­ровности земной поверхности); 3) определения высот пикетов;

4) обобщения рельефа, возникающие из-за неоднородности ската между пикетами;

5) несо­вершенства средств вычисления отметок точек.

Вторая группа - погрешности, вызывающие плановое смещение горизонтали. Точность высотного положения горизонтали в этом случае за­висит от угла наклона топографической поверхности:

1) построения планового обоснования;

2) нанесения пикетов на план;

3) интерполирования и проведения горизонталей;

4) вычерчивания го­ризонталей;.

Точность положения горизонтали по высоте за­висит главным образом от погрешностей обобщения рельефа при съемке. Горизонтали получают на плане путем линейного интерпо­лирования между высотами пикетов. Однако в результате интерполирования мы имеем точку высотой , а не точку земной поверхности с высо­той (рис.1). Разность назовается истинной погрешностью обобщения рельефа при производстве съемки.

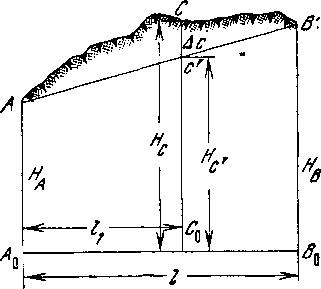
Рис. 1. Обобщение рельефа при съемке

Средняя квадратическая погрешность при съемке вследствие обобщения рельефа, вычисляется по формуле ,

где - коэффициент случайного влияния обобщения рельефа при съемке, приведенный к длине в 1 м; - расстояние между пикетами, выраженное в метрах.Величина коэффициента за­висит от характера рельефа и ко­леблется в пределах 0,01—0,02. Для промышленно-гражанского строительства принято = 0,012.

Из расчета численных зна­чении погрешностей, влияющих на точность положения горизонталей получены многочисленные формулы для оценки точно­сти положения горизонталей по высоте и определения отметок то­чек по плану.

1. Формула проф. Н. Г. Видуева для вычисления средней квадратической погрешности ( С.К.П.) положения горизонтали по высоте:

где - высота сечения рельефа, - знаменатель масштаба плана,

- средний уклон местности.

2. Формула проф. В. Д. Большакова для вычисления ( С.К.П.) определения высоты точки по горизонталям плана:

где - высота сечения рельефа, - коэффициент случайного влияния обобщения рельефа при съемке, - расстояние между пикетами при съемке рельефа, =0,03м; = 0,7 мм на плане, - знаменатель числен­ного масштаба плана; - коэффициент, колеблю­щийся в пределах 0,010—0,015 для местности с углом наклона