§12. Лінійні однорідні рівняння другого порядку із сталими коефіцієнтами .

Рівняння виду , називається лінійним однорідним рівнянням другого порядку із сталими коефіцієнтами .

Спосіб розв’язування . Складаємо характеристичне рівняння

(4)

Можливі три випадки :

1. якщо дискримінант тобто характеристичне рівняння (4) має два різні корені то загальний розв’язок рівняння (3) буде

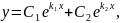де

2. якщо , то

3. якщо , то де , тоді

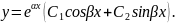
Приклад 1. Знайти загальний розв’язок рівняння

∆ Характеристичне рівняння має дійсні і рівні корені Оскільки це другий випадок , то загальний розв’язок має вигляд

Приклад 2.

∆ Корені характеристичного рівняння комплексні :

Тут , тому загальним розв’язком є функція

Вправи:

101. Серед даних диференціальних рівнянь вкажіть лінійні однорідні другого порядку із сталими коефіцієнтами :

1) =0;

102. Чи є дані функції розв’язками даних рівнянь :

1)

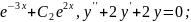
2)

3)

Розв’язати рівняння:

103. ; 104.

105. 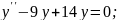106.

107.

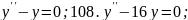
109.

111.

113.

115. Розв’яжіть задачу Коші :

1)

2)

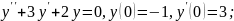
3)

4)

5)

6)

із сталими коефіцієнтами .

§13. Лінійні неоднорідні рівняння другого порядку.

Лінійне неоднорідне рівняння зі сталими коефіцієнтами :

( 5 )

Спосіб розв’язування . Загальний розв’язок ( _з.н.) неоднорідного рівняння (5) дорівнює сумі загального розв’язку _з.о. ) відповідного однорідного рівняння ( 3) і частинного розв’язку( _ч.н. ) рівняння ( 5 ) :

_з.н = _з.о. + _ч.н.

неоднорідного рівняння шукається по вигляду правої частини

Приклади:

1. Якщо _ч.н. = не є коренем характеристичного рівняння (4) ; _ч.н. = _ч.н. = , коли є кратним коренем рівняння ( 4 ) . - шуканий коефіцієнт .

2. Якщо , то частинний розв’язок шукають у вигляді _ч.н. = або _ч.н. , якщо система відносно невідомих коефіцієнтів у першому випадку несумісна .

3. Якщо або

_ч.н. = 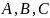- невідомі коефіцієнти , які треба відшукувати , підставляючи _ч.н. в (5) і розв’язуючи систему , складену порівнянням коефіцієнтів при однакових степенях .

Приклад. Розв’язати рівняння :

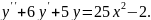
Розв’язання . Спочатку знаходимо загальний розв’язок однорідного рівняння що відповідає даному неоднорідному рівнянню. Його характеристичне рівняння = -1. Тому _з.о. =

Дальше знаходимо частинний розв’язок даного неоднорідного рівняння . Для правої частини даного рівняння згідно вказаного правила ( випадок 1, число і не є коренем характеристичного рівняння ) , многочлен другого степеня :

= _ч.н. = .

Звідси , диференціюючи , знаходимо в дане рівняння , одержимо рівність

або

одержимо систему

із якої знаходимо

Отже , , а шуканий загальний розв’язок даного неоднорідного рівняння .

Вправи:

Розв’язати рівняння:

116. , 117.

118. 119.

120. 121.

122. 123.

124. 125.

126. 127.