
- •§1.Поняття про диференціальні рівняння
- •§2. Приклади задач , що приводять до диференціальних рівнянь .
- •§ 3. Диференціальні рівняння першого порядку з відокремленими змінними .
- •§4. Диференціальні рівняння першого порядку з відокремлюваними змінними .
- •§5. Однорідні диференціальні рівняння першого порядку
- •§6. Лінійні диференціальні рівняння першого порядку .
- •Алгоритм розв’язання
- •§7.Рівняння , які зводяться до лінійних . Рівняння Бернуллі та Ріккаті .
- •8. Рівняння в повних диференціалах .
- •Деякі застосування диференціальних рівнянь першого порядку .
- •Запитання для самоконтролю:
- •Диференціальні рівняння вищих порядків.
- •§10.Основні поняття та означення . Задача Коші.
- •§11.Простіші диференціальні рівняння другого порядку .
- •§12. Лінійні однорідні рівняння другого порядку із сталими коефіцієнтами .
- •§13. Лінійні неоднорідні рівняння другого порядку.
- •Запитання для самоконтролю
- •Системи диференціальних рівнянь
- •§14.Нормальні системи рівнянь .
- •Список літератури
Запитання для самоконтролю:
Яке рівняння називається диференціальним ? Наведіть приклади .
Яка функція називається розв’язком диференціального рівняння ?
Який розв’язок диференціального рівняння називається загальним і який - частинним ?
Який геометричний зміст загального і частинного розв’язку диференціального рівняння ?
Чи може диференціальне рівняння мати скінченне число розв’язків ?
Що таке порядок диференціального рівняння і як його визначити ?
Чи можуть інтегральні криві диференціального рівняння перетинатися?
Як перевірити чи правильно знайдено розв’язок диференціального рівняння чи ні ?
Чим відрізняється диференціальне рівняння від алгебраїчного рівняння?
Який загальний вигляд диференціальних рівнянь першого порядку з відокремленими змінними і з відокремлюваними змінними ?
Як розв’язуються рівняння з відокремленими змінними ?
В якій послідовності розв’язуються диференціальні рівняння з відокремлюваними змінними ?
В чому полягає задача Коші ? Який її геометричний зміст ?
Який загальний вигляд лінійних диференціальних рівнянь першого порядку ? Як розв’язуються такі рівняння ?
Навести рівняння , звідні до лінійних , та викласти методи їх інтегрування .
Дати означення рівняння Бернуллі . Як воно розв’язується ?
Дати означення рівняння Ріккаті . Як його розв’язати , коли відомо частинний розв’язок ?
Що називається рівнянням в повних диференціалах ?
Диференціальні рівняння вищих порядків.
§10.Основні поняття та означення . Задача Коші.
Розглянемо диференціальні рівняння , які містять похідні вищих порядків . Порядок найвищої похідної невідомої функції , що входить у диференціальне рівняння , називається порядком цього рівняння .
Диференціальне рівняння n-го порядку має вигляд
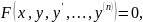 (1)
(1)
де
- незалежна змінна ;
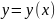 - невідома функція ;
- невідома функція ;
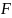 - відома функція .
- відома функція .
Розв’язком
рівняння
(1)
на деякому інтервалі ( а,
b) називається
n
разів
неперервно диференційована функція на
цьому інтервалі функція
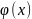 , яка при підстановці в дане рівняння
обертає його в тотожність .
, яка при підстановці в дане рівняння
обертає його в тотожність .
Графік розв’язку диференціального рівняння (1) називається його інтегральною кривою .
Для диференціальних рівнянь вищих порядків , як і для рівнянь першого порядку , розглядається задача Коші або задача з початковими умовами .
Для
рівняння (1) ця задача ставиться так :
серед усіх розв’язків рівняння (1) знайти
такий розв’язок
,
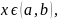 який при
який при
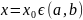 задовольняє
такі умови :
задовольняє
такі умови :
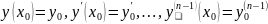 ,
,
де
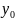 ,
,
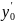 ,
… ,
,
… ,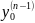 - довільні
наперед задані дійсні числа .
- довільні
наперед задані дійсні числа .
§11.Простіші диференціальні рівняння другого порядку .
Загальний
вигляд
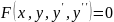 .
(2)
.
(2)
Рівняння , що містить похідні або диференціали другого порядку , називається диференціальним рівнянням другого порядку .
Простішим диференціальним рівнянням другого порядку є рівняння :
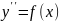
Таке рівняння розв’язується двократним інтегруванням.
Приклад.
Розв’язати рівняння
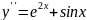 .
.
Розв’язання.
Так
як
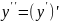 , то інтегруючи праву частину рівняння
, маємо
, то інтегруючи праву частину рівняння
, маємо

Інтегруючи ще раз , одержимо всі разв’язки даного рівняння
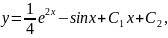 де
де
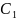 ,
,
 - довільні сталі .
- довільні сталі .
Задача знаходження розв’язку диференціального рівняння другого порядку , що задовольняє початковим умовам
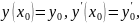 де
де
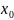 ,
,
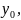 - задані числа , називається задачею
Коші .
- задані числа , називається задачею
Коші .
Ці умови називаються початковими умовами , так як з фізичної точки зору вони означають , що в фіксований ( початковий ) момент часу задані положення матеріальної точки і її швидкість .
Геометричний зміст задачі Коші полягає в знаходженні інтегральної кривої , що проходить через задану точку і має заданий кутовий коефіцієнт дотичної в цій точці .
Вправи
Розв’язати рівняння:
89.
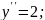 90.
90.
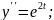
91.
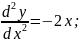 92.
92.
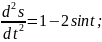
93.
 94.
94.
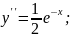
95.
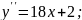 96.
96.
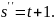
97. Складіть диференціальне рівняння , розв’язками якого є функції :
1)
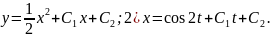
98. Розв’яжіть задачу Коші :
1)
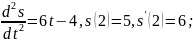
2)
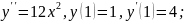
3)
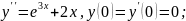
4)
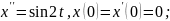
5)
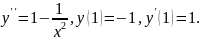
99.
Прискорення
тіла , що рухається прямолінійно ,
змінюється по закону
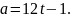 Початкове
положення
Початкове
положення
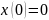 і початкова швидкість v(0)=10
м/с. Знайдіть
закон руху точки , положення і швидкість
в момент
і початкова швидкість v(0)=10
м/с. Знайдіть
закон руху точки , положення і швидкість
в момент
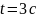 ; момент часу коли швидкість буде
найменшою .
; момент часу коли швидкість буде
найменшою .
100. Тіло вільно падає на Землю без початкової швидкості з висоти 1000м . Знайдіть закон вільного падіння тіла . Через скільки часу тіло досягне Землі ?
