8. Рівняння в повних диференціалах .

Рівняння виду називається рівнянням в повних диференціалах , якщо його ліва частина є його повним диференціалом деякої функції u(x,y) , тобто

Для того , щоб рівняння було в повних диференціалах , необхідно і достатньо , щоб .

Приклад. Розв’язати рівняння :

Розв’язання . Спочатку переконаємось , що дане рівняння є рівнянням в повних диференціалах :

Знаходимо невизначені інтеграли :

вважаючи сталою ,

вважаючи сталою.

Беручи всі відомі члени із першого результату і дописавши до них члени яких не вистачає , що залежать тільки від , із другого результату , одержимо функцію , повним диференціалом якого є ліва частина даного диференціального рівняння , а прирівнявши її до довільної сталої , одержимо шуканий загальний інтеграл даного рівняння :

Вправи

Розв’язати рівняння:

74. ;

75.

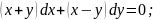
76.

77. (

78.

79.

80.

81.

82.

83.

Деякі застосування диференціальних рівнянь першого порядку .

В різних сферах людської діяльності характер задач , які зводяться до диференціальних рівнянь , та методику розв’язування їх можна схематично описати так . Відбувається деякий процес , наприклад , фізичний , хімічний , біологічний . Нас цікавить певна функціональна характеристика даного процесу , тобто залежність від часу , температури тіла , яке охолоджується , або кількості речовини , яка утворюється в результаті хімічної реакції , або кількості бактерій , які вирощуються за певних умов. Якщо повна інформація про хід цього процесу є достатньою, то можна спробувати побудувати його математичну модель. У багатьох випадках такою моделлю буде диференціальне рівняння, одним із розв’язків якого і є шукана функціональна залежність.

Приклади:

1. ( Про розмноження бактерій ). У сприятливих для розмноження умовах знаходиться деяка кількість N₀ бактерій . Знайти залежність збільшення числа бактерій від часу , якщо швидкість розмноження бактерій пропорційна їх кількості .

∆ Позначимо через N (t) кількість бактерій в момент часу t . Тоді - швидкість розмноження . За умовою

Коефіцієнт залежить від виду бактерій та умов , яких вони знаходяться. Його визначають експериментально . Інтегруючи знайдене рівняння дістанемо його загальний розв’язок : тому

2. ( Про радіоактивний розпад .) Експериментально встановлено , що швидкість радіоактивного розпаду речовини пропорційна її кількості в даний момент часу . Вказати закон зміни маси речовини від часу , якщо при t=0 маса речовини дорівнювала .

∆ Нехай маса речовини в момент часу t . За умовою

де - коефіцієнт пропорційності . Знак мінус береться тому ,що з часом кількість речовини зменшується . Розв’язуючи знайдене рівняння , дістанемо що

3. (Про охолодження тіла .) Згідно із законом Ньютона , швидкість охолодження тіла пропорційна різниці між температурою тіла і температурою навколишнього середовища .

∆ Відомо , що нагріте до температури тіло помістили в середовище , температура якого стала і дорівнює . Знайти залежність температури тіла від часу .

∆ Нехай в момент часу t температура тіла дорівнює (t) . За умовою

(знак мінус вказує на зменшення температури ). Відокремлюючи змінні та інтегруючи , маємо

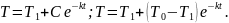
4. ( Про силу струму .) Треба знайти залежність сили струму від часу в контурі , який має електрорушійну силу , опір R та індуктивність L , де - сталі.

∆ Згідно з законом Ома , маємо

Розв’язуючи це лінійне рівняння заміною 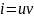, дістанемо загальний розв’язок 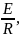де С – довільна стала . При маємо тому

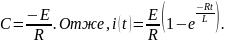
Звідки видно , що сила струму при наближається до свого стаціонарного значення

Вправи:

84. Тіло , яке мало в початковий момент часу ( ) температуру ⁰ , охолоджується в повітряному середовищі до температури ₁=60⁰ на протязі часу ₁=20 хв. Знайти час , за який тіло охолоджується до температури 30⁰ , якщо відомо , що температура повітря 20⁰ , а швидкість охолодження тіла пропорційна різниці між температурою тіла і температурою повітря .

85. Знайти закон руху тіла , яке рухається прямолінійно із швидкістю , якщо відомо , що за час тіло проходить шлях

86. Швидкість розпаду радію в момент часу пропорційна його кількості Нехай в початковий момент часу маса радію ₀ = 200г. Скільки радію залишиться через 300 років , якщо відомо , що період піврозпаду радію дорівнює 1150 рокам .

87. Катер рухається в спокійній воді із швидкістю Визначте швидкість катера через 2 хв після виключення двигуна , якщо за 40 с вона зменшилася до Потужність води пропорційна швидкості руху катера .

88. Конденсатор , ємкість якого Q , включається в коло з напругою Е і потужністю R . Визначте заряд q(t ) конденсатора в момент часу t , якщо в початковий момент часу він був рівний нулю .