Теплота Томпсона Qт равна

(8.21)

где тау — коэффициент Томпсона.

5. Гальваномагнитные эффекты в полупроводниках

Гальваномагнитными эффектами в полупроводниках называются такие явления, которые возникают при одновременном действии на полупроводник электрического и магнитного полей.

Все гальваномагнитные эффекты делятся на поперечные (действие электрического и магнитного полей обнаруживается на гранях полупро­водника, параллельных электричес­кому и магнитному полям) и продоль­ные (проявляются вдоль образца).

К поперечным относятся эффекты Холла и Эттинсгаузена, к параллель­ным—изменение сопротивления образ­ца в магнитном поле и эффект Нернста (продольная разность температур).

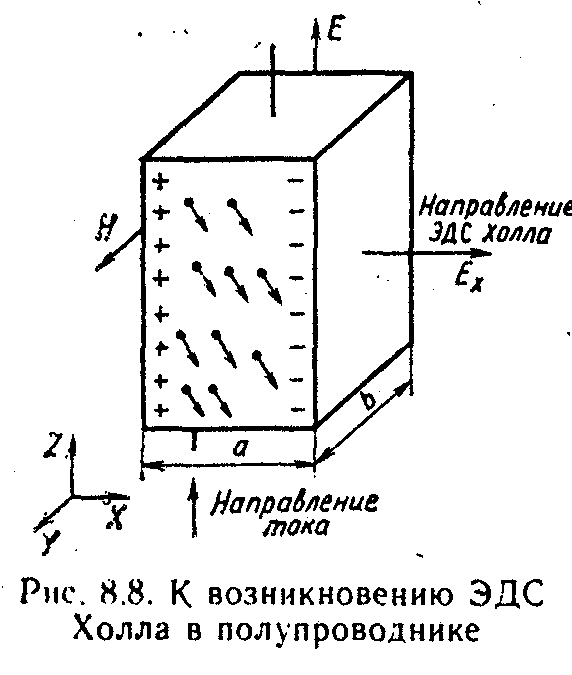
Рассмотрим только эффект Холла. Если полупроводник, вдоль которого течет электрический ток, поместить в магнитное поле, перпендикулярное

направлению тока, то в полупроводнике возникнет поперечное электрическое поле, перпендикулярное току и магнитному полю. Это явление получило название эффекта Холла, а возникающая по­перечная ЭДС — ЭДС Холла.

На рис. 8.8 изображена пластинка полупроводника n-типа. Электрическое поле Е направлено параллельно оси Z, а магнитное

поле Н — вдоль оси У. На движущийся в магнитном поле электрон действует сила Лоренца, которая отклоняет его в направлении, перпендикулярном направлению магнитного поля. В результате электроны будут накапливаться у одного из торцов образца. На противоположной грани будет создаваться положительный нескомпенсированный заряд, обусловленный ионами донорной приме­си. Такое накопление зарядов будет происходить до тех пор, пока действие возникшего в результате такого процесса электрического поля не уравновесит действующую на электрон силу Лоренца. Ус­ловие равновесия действующей на электрон силы в скалярной фор­ме можно записать в виде

где Vn — средняя скорость направленного движения электрона;

В — магнитная индукция в образце; Ex — напряженность воз­никшего поперечного электрического поля.

Считая поперечное электрическое поле однородным, получим

(8.23)

где а — ширина пластинки; Ux — ЭДС Холла. Известно также, что j = сигмаЕ или

(8.24)

где j=I(ab) - плотность тока, протекающего в образце, под дей­ствием внешнего электрического поля Е.

Используя (8.24), из (8.22) получаем

(8.25)

Величина Rx называется коэффициентом Холла и определяется

как

(8.26)

ЭДС Холла в полупроводнике n-типа можно определить по формуле

Знак минус отражает тот факт, что носителями заряда в данном полупроводнике являются электроны. Для полупроводников р-типа получается аналогичное выражение, только лишь концентра­ция п будет заменена на р и направление поперечного электрическо­го поля будет противоположным, т. е. ЭДС Холла будет положи­тельная. Это обстоятельство используется для определения типа электропроводности полупроводников.

Если выразить ток в А, напряженность магнитного поля — в А/м, холловское напряжение — в В, толщину образца — в см, то коэффициент Холла равен (cm³ /k)

Таким образом, измерив разность потенциалов Холла Ux при из­вестном токе I, напряженности магнитного поля Н и толщине образ­ца b рассчитываем Rx. Далее, если известны коэффициент Холла Pх и электропроводность, легко вычислить концентрацию носителей заряда и величину подвижности.

Эффект Холла интересен не только как метод определения харак­теристик полупроводниковых материалов, но и как принцип дейст­вия целого ряда полупроводниковых приборов, нашедших техниче­ское применение.