1.7. Питання для самоконтролю

1. Охарактеризуйте розрахунок електричних кіл методом еквівалентних перетворень та приведіть приклад його застосування.

2. Охарактеризуйте способи з’єднання елементів електричних кіл – послідовне, паралельне, змішане. З’єднання “трикутником” та “зіркою”.

3. Приведіть приклади доцільності перетворення сполучення “зіркою” в еквівалентне сполучення “трикутником” і навпаки.

4. Охарактеризуйте основні етапи розрахунку електричних кіл методом безпосереднього застосування законів Кірхгофа.

5. Дайте визначення вітки, незалежного контуру складного електричного кола та проаналізуйте, скільки рівнянь можна скласти за другим законом Кірхгофа.

6. Проаналізуйте розрахунок електричних кіл, методом законів Кірхгофа. Визначте для складного електричного кола кількість рівнянь, які можна скласти за першим та другим законами Кірхгофа.

7. Приведіть основні етапи розрахунку електричних кіл методом контурних струмів.

8. Сформулюйте принцип накладання. Приведіть порядок розрахунку електричних кіл методом еквівалентних перетворень та методом накладання.

9. Приведіть порядок розрахунку електричних кіл методом двох вузлів.

10. Приведіть рівняння балансу потужності в електричних колах. та поясніть його фізичний зміст.

2. Розрахунок електричних кіл в режимі усталених гармонічних коливань

Для розрахунку та аналізу радіоелектронних кіл в режимі усталених гармонічних коливань використовують методи, розроблені для режиму постійного струму. Для випадку, коли окремі вітки кола синусоїдного струму не зв’язані між собою магнітно, в розрахункових формулах замість постійної ЕРС E слід підставляти комплексну ЕРС , замість постійного струму – комплексне значення струму , замість опору R – комплексний опір .

2.1. Представлення синусоїдних функцій часу комплексними числами

Комплексний метод об’єднує простоту векторних діаграм з можливістю проводити розрахунки з будь-якою точністю і базується на представленні векторів на комплексній площині і запису їх комплексними числами. Це дає можливість для радіоелектронних кіл синусоїдного струму застосувати закони Ома та Кірхгофа і методи розрахунку кіл як і для кіл постійного струму.

Кожному вектору на комплексній площині відповідає певне комплексне число, яке можна записати в алгебраїчній, тригонометричній та показниковій формах.

Комплексна площина є прямокутною системою координат. Вісь абсцис на комплексній площині є віссю дійсних чисел і позначається (+) (-), а вісь ординат (+j) (-j), де .

По осі дійсних чисел відкладають дійсну частину комплексного числа, по осі ординат – уявну частину (рисунок 3.6).

Комплексну величину відзначають точкою або підкреслюють знизу ( і т.д.) Комплексним числом вважають суму дійсної та уявної складових.

,

де - модуль комплексного числа, аргумент комплексного числа. Співвідношення

,

формула Ейлера, – основа натуральних логарифмів. У загальному вигляді

,

так як .

Якщо вектор повернути з положення 1 в положення 2, то в комплексній формі це запишеться як

.

Таким чином множення комплексного числа на множник типу рівноцінно повороту вектора на комплексній площині на кут .

Тому множник називають оператором повороту вектора.

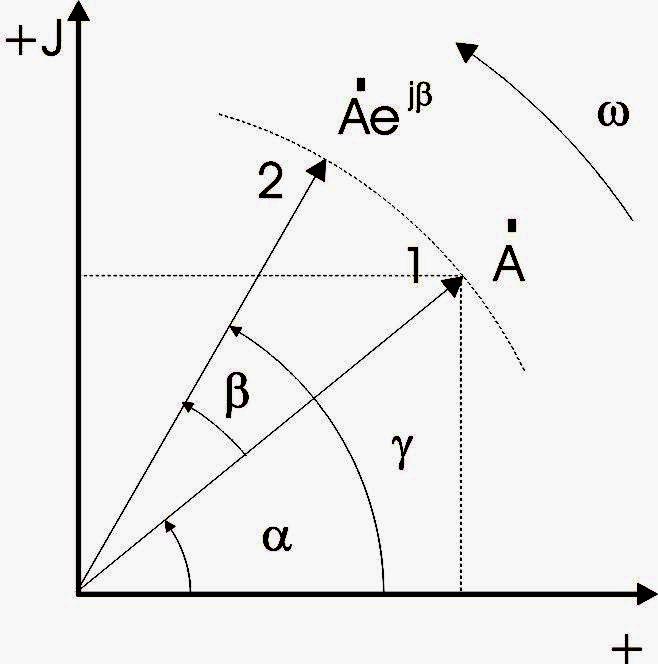
Рисунок 2.1 – Представлення синусоїдної функції часу

комплексним числом

Нехай . Тоді

,

тобто множення комплексного числа на рівноцінно повороту вектора на комплексній площині на кут . Приймаючи кут функцією часу , одержують оператор обертання вектора . ( – комплексна функція часу).

Похідна від комплексної функції часу рівна

.

Інтеграл від комплексної функції часу

.

З приведених виразів видно, що диференціювання та інтегрування комплексних функцій часу можна замінити відповідно множенням та діленням їх на .