Тема № 5. Транспортная задача.

Особенности экономико-математической модели транспортной задачи. Нахождение первоначального допусти­мого плана перевозок методами "северо-западного угла" и "минималь­ного элемента". Поиск оптимального решения распределительным методом. Открытая модель транспортной задачи.

Содержание основных понятий темы

Формулировка транспортной задачи.

Пусть имеется m пунктов отправления (или пунктов производства) А₁, А₂, ..., А_m и n пунктов назначения (потребления) B₁, B₂, ..., В_n. Обозначим ресурсы груза в i-м пункте отправления через a_i, (i=l,…,m), а потребности каждого j-ro пункта потребления через b_j (j=l,…,n). Известна стоимость доставки единицы груза от каждого i-ro пункта отправления до каждого j-ro пункта назначения -с_ij,. Будем предполагать, что общее количество грузов, имеющихся на пунктах отправления равно потребности в нём на пунктах назначениях, т.е. имеется следующее соотношение:

Требуется определить, какое количество груза необходимо перевезти из каждого i-ro пункта отправления до каждого j-ro пункта назначения чтобы:

• вывезти грузы всех поставщиков;

• удовлетворить всех потребителей;

• достигнуть экстремума целевой функции.

Постановка задачи и выбор критерия оптимальности.

Так как необходимо вывезти весь груз с каждого пункта отправления то должны выполняться равенства:

x₁₁ + x₁₂ + ... + х_1n = а₁

x₂₁ + x₂₂ + ... + x_2n = a₂

_{.........................................................}

x_m1 + x_m2 + ... +x_mn = a_m

В каждый пункт назначения должен быть завезен весь требуемый груз, поэтому должны выполняться равенства:

x₁₁ + x₂₁ + ... + x_m1 = b₁

x₁₂ + x₂₂ + ... + x_m2 = b₂

....................................

x_m1 + x_m2 + ... + x_mn = b_n

Построение математической модели.

Оптимизируемым функционалом в данной задаче являются суммарные приведенные затраты на доставку всего груза отправления потребителю

F = c₁₁ х₁₁ + c₁₂ х₁₂ + ... +c_mn x_mn → min

Таким образом, задача свелась к нахождению таких значений переменных, которые удовлетворяют двум вышеприведенным равенствам и минимизируют суммарные приведенные затраты на доставку груза от отправителя к потребителю.

Задача 1.

Построить экономико-математическую модель следующей задачи. Имеется три поставщика и че­тыре потребителя. Мощности поставщиков и спросы по­требителей, а также затраты на перевозку единицы груза для каждой пары «поставщик-потребитель» сведены в таб­лицу поставок.

Поставщики	Мощности поставщиков	Потребители и их спрос
		1	2	3	4
		20	110	40	110
1	60	1 х11	2 х12	5 х13	3 х14
2	120	1 х21	6 х22	5 х23	2 х24
3	100	6 х31	3 х32	7 х33	4 х34

Решение:

Искомый объем перевозки от i-гo поставщика к j-му потребителю обозначим через хij и назовем постав­кой клетки (i, j). Например, х₁₂ - искомый объем перевоз­ки от 1-го поставщика ко 2-му потребителю или поставка клетки (1, 2) и т.д. Заданные мощности поставщиков и спросы потребителей накладывают ограничения на значе­ния неизвестных xij. Так, например, объем груза, забирае­мого от 1-го поставщика должен быть равен мощности этого поставщика - 60 ед. т.е. х₁₁+х₁₂+х₁₃+х₁₄=60 (уравнение баланса по первой строке). Таким образом, чтобы мощность каждого из поставщиков была реализова­на, необходимо составить уравнение баланса для каждой строки таблицы поставок, т.е.

Аналогично, чтобы спрос каждого из потребителей был удовлетворен, подобные уравнения баланса составляем для каждого столбца таблицы поставок:

Очевидно, что объем перевозимого груза не может быть отрицательным, поэтому следует дополнительно предположить, что

Суммарные затраты F на перевозку выражаются через коэффициенты затрат и поставки следующим образом:

F=1x₁₁+2x₁₂+5x₁₃+1x₂₁+6x₂₂+5x₂₃+2x₂₄+6x₃₁+3x₃₂+7x₃₃+4x₃₄.

Итак, математическая формулировка за­дачи: на множестве неотрицательных решений системы ограничении, составленным по строкам и столбцам, найти такое решение X=(x₁₁, x₁₂, …, x₃₃, x₃₄) при котором линейная функция F при­нимает минимальное значение.

Исследование математической модели.

Исследование и решение транспортной задачи, как правило, проводят в два этапа. На первом этапе находят какое-нибудь (хотя бы неудачное) решение, далекое от оптимального, но удовлетворяющее совокупности линейных неравенств (ограничений), или убеждаются, что этого решения нет. Этот этап называется отысканием опорного (начального) плана.

На втором этапе производится последовательное улучшение этого плана по определенным правилам до тех пор, пока дальнейшее улучшение станет невозможным. От того, каким будет опорный план, зависит время решения транспортной задачи на втором этапе решения.

Задача 2.

Найти первоначальное базисное распреде­ление поставок для транспортной задачи 1. методом «северо-западного» угла.

Решение. Дадим переменной х₁₁ максимально возмож­ное значение или, иными словами; максимально возмож­ную поставку в клетку (1,1) - «северо-западный» угол таблицы поставок х₁₁= min {60; 20} = 20. После этого спрос 1-го потребителя будет полностью удовлетворен, в результате чего первый столбец таблицы поставок выпа­дет из последующего рас­смотрения. В оставшейся таблице найдем новый «северо-западный» угол - клетку (1, 2) и дадим в нее максимально возмож­ную поставку. Учитывая, что 1-й поставщик уже отдал 20 ед. груза и у него осталось только 40 = 60 - 20 ед. груза, получаем х₁₂ = min{40; 110} = 40.

После этого мощность первого поставщика полностью реализована, из рассмотрения выпадает первая строка таб­лицы поставок.

В оставшейся таблице снова находим «северо-западный» угол и т.д. В ре­зультате приходим к рас­пределению поставок, приведенному в таблице.

	20	110	40	110
60	1 20	2 40	5	3
120	1	6 70	5 40	2 10
100	6	3	7	4 100

Существенный недостаток метода «ceвepo-западного» угла состоит в том, что он построен без учета значений коэф­фициентов затрат задачи. Однако данный метод допускает модификацию, лишенную этого недостатка. Такой метод получения опорного плана называется методом наименьших затрат.

Метод наименьших затрат.

Сущность метода минимального элемента и состоит в выборе клетки с наи­меньшим коэффициентом затрат. На каждом шаге максимально возможную поставку следует давать не в «севе­po-западную» клетку оставшейся таблицы, а в клетку с наи­меньшим коэффициентом затрат. Следует отметить, что этот метод, как правило, позволяет найти опорный план транспортной задачи, при котором общая стоимость перевозок груза меньше, чем общая стоимость перевозок при плане, найденном для данной задачи с помощью метода северо-западного угла. Поэтому наиболее целесообразно опорный план транспортной задачи находить методом наименьших затрат.

Задача3.

Методом наименьших затрат найти перво­начальное распределение поставок в транспортной задаче 1.

Решение. В таблице поставок имеются две клетки с наименьшим коэффициентом затрат: (1, 1) и (2, 1). Более того, совпадают максимально возможные поставки для этих клеток: х₁₁= min {60; 20}= 20, х₂₁= min {120; 20} = 20. Поэто­му поставку можно дать в любую из этих клеток, например, в клетку (2, 1): х₂₁= 20. В результате первый столбец табли­цы поставок выпадает из последующего рассмотрения. В оставшейся таблице вновь две клетки имеют наи­меньший коэффициент затрат: (1, 2) и (2, 4). Заполняем ту из них, которая допускает наибольшую поставку: х₂₄= min {120 - 20; 110} = 100 (х₁₂ = min {60; 110} = 60). При этом из рассмотрения вы­падает вторая строка табли­цы поставок Аналогично продолжая за­полнение таблицы поста­вок шаг за шагом, получаем x₁₂=min{60; 110}=60, х_З2 = min{100; 110 - 60}=50, , х₃₄= min{110-50; 110 - 100} = 10, х₃₃= min {100-60; 40}=40.

	20	110	40	110
60	1	2 60	5	3
120	1 20	6	5	2 100
100	6	3 50	7 40	4 10

Критерии оптимальности базисного распределения поставок.

Каждому базисному распределению поставок соответствует разбиение переменных задачи на свободные (они соответствуют свободным клеткам и только им) и базисные. Коэффициент β_ij при свободной переменной xij в выражении целевой функции F через свободные переменные называется оценкой свободной клетки (i,j). Транспорт­ная задача - задача на минимум. Критерий опти­мальности транспортной задачи: базисное распределение поставок оптимально тогда и только тогда, когда оценки всех свободных клеток неотрицательны.

Экономический смысл оценки свободной клетки: Оценка β_ij свободной клетки (i,j) равна приращению ∆F суммарных затрат на перевозку при переводе в клетку (i,j) единичной поставки.

Оценка свободной клетки нe изменится, если к коэффициентам затрат некоторой строки (столбца) таб­лицы поставок прибавитъ некоторое число.

Число, прибавляемое к коэффициентам затрат выде­ленной строки (столбца) называется поmенциалом данной строки (столбца). Поэтому приведенная теорема называ­ется также теоремой о потенциалах.

Правило нахождения оценок свободных клеток: к коэффициентам затрат таблицы по­ставок в каждой строке и столбце надо прибавить такие числа (потенциалы), чтобы коэффициенты затрат во всех заполненных клетках стали равными нулю. Полученные при этом коэффициенты затрат свободных клеток равны оценкам этих клеток.

Задача 4.

Найти оценки свободных клеток базис­ного распределения поставок, приведенные в таблице.

	20	110	40	110
60	1	2 60	5	3
120	1 20	6	5	2 100
100	6	3 50	7 40	4 10

Решение.

Изменение коэф­фициентов затрат можно начинать с любого столбца (строки). Потенциал столб­ца (строки), избранного для начала, может быть произвольным, но можно доказать, что после его фиксации потенциалы ос­тальных строк и столбцов будут определены одно­значно.

Начнем с первого столбца. Пусть его потенциал равен нулю. Рядом с потенциалом в скобках записы­ваем номер шага (поставки опускаем).

1	2	5	3
1	6	5	2
6	3	7	4

0(1) 0(6) -4(5) -1(3)

После прибавления этого потенциала к коэффициен­там затрат первого столбца коэффициент затрат заполнен­ой клетки (2, 1) не изменится. Чтобы полученный после сложения коэффициент затрат этой клетки стал равен нулю, потенциал второй строки таблицы должен быть ра­вен -1. Для обнуления коэффициента затрат клетки (2, 4) потенциал четвертого столбца должен быть равен -1 т.д.

Измененные коэффициенты затрат удобно выписать в виде отдельной матрицы оценок

.

Элементы матрицы оценок, соответствующие свободным клеткам таблицы поставок, равны оценкам этих сво­бодных клеток. Так как среди элементов матрицы оценок есть отрицательные, то распределение поставок не оптимально. Набор потенциалов, с помощью которых находится мат­рица оценок, не единственен. Для каждого базисного распределения матрица оценок определен однозначно.

Распределительный метод решения транспортной за­дачи.

Пусть исходное распределение поставок не оптималь­но. Тогда осуществляется переход к новому распределению поставок так, что одна из свободных клеток становится за­полненной, а одна из заполненных - свободной.

Задача 5.

В распределении поставок, приведенном в таблице передать единичную поставку в клетку (1, 3).

	20	110	40	110
60	1	2 60	5	3
120	1 20	6	5	2 100
100	6	3 50	7 40	4 10

Решение.

Давая единичную поставку в клетку (1,3), следует изменить поставки в заполненных клетках так, чтобы сохранился баланс по строкам и столбцам. (Будем полагать, что во всех свободных клетках, отличных от клетки (1, 3), поставка останется нулевой.) Тогда для того чтобы 3-й поставщик отправил по-прежнему 100 ед. груза, поставку в клетку (3, 2) увеличиваем на единицу; 2-му по­требителю нужно только 110 ед. груза, поэтому поставку в клетку (1, 2) придется уменьшить на единицу. Полученное распределение поставок представлено в таблице.

	20	110	40	110
60	1	2 59	5 1	3
120	1 20	6	5	2 100
100	6	3 51	7 39	4 10

(1,2)

2 -

(1,3)

5 +

( 3,2)

3 +

(3,3)

7 -

(Заметим, что найденный вариант перераспределения поставок, единствен). Что касается самой переда­чи поставки, то она производится по циклу (дополнительно в клетках цикла расставлены знаки «+» или «-« в зависимости от того, увеличивается или уменьшается величина по­ставки клетки).

В общем случае циклом в матрице называется ломаная с вершинами в клетках и звеньями, лежащими вдоль строк и столбцов матрицы, удовлетворяющая условиям:

- ломаная должна быть связной, т.е. из любой ее вер­шины можно попасть в любую другую вершину по звень­ям ломаной;

- в каждой вершине ломаной встречаются два звена, одно из которых располагается по строке, другое – по столбцу.

Циклом пересчета называется такой цикл в таблице с базисным распределением поставок, одна из вершин кото­рого лежит в свободной клетке, остальные - в заполнен­ных. Цикл пересчета называется означенным, если в его вершинах расставлены знаки «+» или «-« так, что в сво­бодной клетке состоит знак «+», а соседние вершины име­ют противоположные знаки.

Для каждой свободной клетки базисного распределе­ния поставок существует единственный цикл пересчета.

Алгоритм распределительного метода решения транспортной задачи.

1. Для данного базисного распределения поставок нахо­дим матрицу оценок

2. Если оценки всех свободных клеток неотрицательны найденное распределение оптимально - решение законче­но. Если среди оценок свободных клеток есть отрицательные, то выбираем одну из них для передачи в нее поставки (для определенности можно брать, например, одну из кле­ток с наименьшей оценкой).

3. Для избранной свободной клетки строится означен­ный цикл пересчета. Поставка z, передаваемая по циклу, определяется как минимум среди Поставок клеток постро­енного цикла со знаком «-«. Найденная поставка передви­гается по циклу. При этом поставка в клетках цикла со знаком «+» увеличивается на z, а в клетках со знаком «-« уменьшается на z. Клетка, поставка в которой при этом станет равной нулю, будет считаться свободной; осталь­ные клетки цикла - заполненными. Таким образом, полу­чено новое базисное распределение поставок.

4. Переходим к п. 1 алгоритма.

Задача 6.

Решить транспортную задачу 1, применив распределительный метод.

Решение.

В качестве исходного, возьмем базисное рас­пределение поставок, полученное методом наименьших затрат, приведенное в таблице.

	20	110	40	110
60	1	2 60	5	3
120	1 20	6	5	2 100
100	6	3 50	7 40	4 10

Это распре­деление не оптимально. Перейдем к новому базисному распределению, передавая поставку в одну из клеток с отрицательной оценкой, например в клет­ку (1,3).

Размер этой поставки равен минимуму Поставок клеток со знаком «-« цикла (т.е. клеток (1, 2) и (3, 3)): Х_1З = min{60; 40} = 40. В результате передвижения этой по­ставки по циклу (см. таблицу ниже) клетка.(3,3) становится свободной.

	20	110	40	110
60	1	2 59	5 1	3
120	1 20	6	5	2 100
100	6	3 51	7 39	4 10

(1,2)

2 -

(1,3)

5 +

( 3,2)

3 +

(3,3)

7 -

Поставка клетки (3, 2) (клетки цикла со зна­ком «+») увеличивается на 40 ед., а клетки (1,2) (клетки со знаком «-«) уменьшается на 40 ед. Новое распределе­ние поставок приведём в таблице.

	1 20	5 40	3
1 20	6	5	2 100
6	3 90	7	4 100

0 0 -3 -1

Найдем матрицу оценок распределения поставок для этого, подберем потенциалы так, чтобы ко­эффициенты затрат заполненных клеток стали равными нулю. Тогда матрица оценок примет вид .

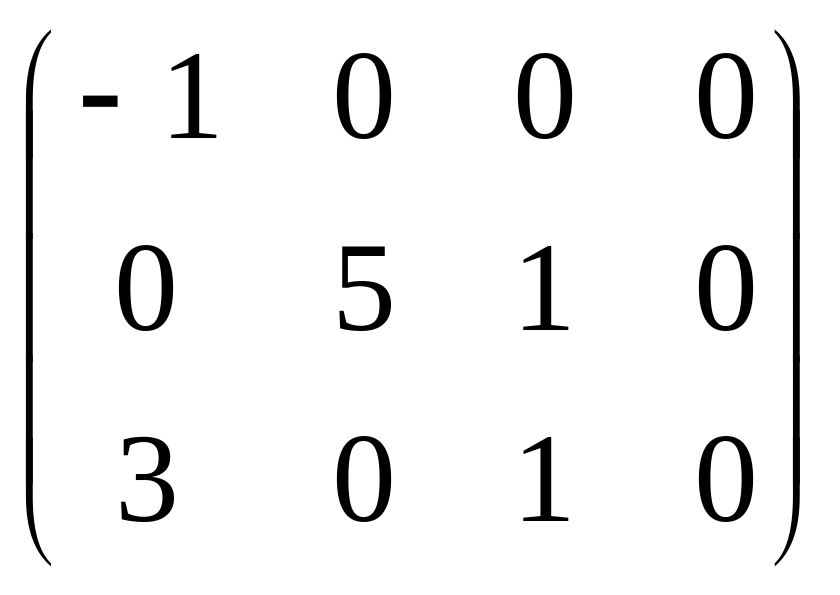Так как среди свободных клеток есть клетка (1, 1) с от­рицательной, оценкой, то найденное распределение не опти­мально и передача поставки в клетку (1, 1) ведет к умень­шению суммарных затрат на перевозку. Означенный цикл пересчета для клетки (1,1) приведем ниже.

(1,1)

+

(1,2)

- 20

( 2,1)

- 20

(2,4)

+ 100

(3,2)

+ 90

( 3,4)

- 10

Поставка, передаваемая по это­му циклу, Х₁₁ = min{20; 20; 10} = 10. Новое распределение поста­вок приведем в таблице.

1 10	2 10	5 40	3
1 10	6	5	2 110
6	3 110	7	4

Матрица оценок этого распределения не имеет отрицательных элементов, поэтому данное распределение оптимально.

Суммарные затраты на перевозку в данном случае составляют

F min = 1* 10 + 2 * 10 + 5*40 + 1 * 10 + 2 * 110 + 3* 100 = 760 (ден. ед.).

Открытая транспортная задача решается сведением к закрытой с помощью фиктивного поставщика (потребителя).

Задача 7.

Привести открытую транспортную задачу, представленную в таблице, к закрытой.

Поставщики	Мощности поставщиков	Потребители и их спрос
		1	2	3	4
		100	250	50	10
1	200	5	8	9	1
2	190	3	7	9	2
3	100	5	8	3	9

Решение.

1. Найти суммарную мощность поставщиков .

2. Найти суммарный спрос потребителей .

=100+250+50+10=410.

3. Сравнить полученные суммы. > (490>410).

4. Если мощности поставщиков больше спроса потребителей, то вычислить разность:

R=490-410=80.

5. Ввести «фиктивного потребителя» с потребностью, равной R.

Вводим «фиктивного потребителя» с номером 4 и потребностью, равной 80.

6. Ввести дополнительный столбец в таблицу. Вводим дополнительный пятый столбец.

7. Коэффициенты затрат в новом столбце принять равными нулю (c_ij=0).

Полагаем все c_i5=0, i=1,2,3.

8. Составить новую таблицу.

Результаты представлены в таблице.

Поставщики	Мощности поставщиков	Потребители и их спрос
		1	2	3	4	5
		100	250	50	10	80
1	200	5	8	9	1	0
2	190	3	7	9	2	0
3	100	5	8	3	9	0

Задача 8.

Привести открытую транспортную задачу, представленную в таблице, к закрытой.

Поставщики	Мощности поставщиков	Потребители и их спрос
		1	2	3	4
		50	50	40	60
1	30	5	4	6	4
2	70	4	5	5	8
3	70	7	3	4	7

Решение.

1. Найти суммарную мощность поставщиков .

2. Найти суммарный спрос потребителей .

=50+50+40+60=200.

3. Сравнить полученные суммы. < (170<200).

4. Если мощности поставщиков больше спроса потребителей, то вычислить разность:

R=200-170=30.

5. Ввести «фиктивного потребителя» с потребностью, равной R.

Вводим «фиктивного потребителя» с номером 4 и потребностью, равной 30.

6. Ввести дополнительный столбец в таблицу. Вводим дополнительный пятый столбец.

7. Коэффициенты затрат в новом столбце принять равными нулю (c_ij=0).

Полагаем все c_j4=0, j=1,2,3.

8. Составить новую таблицу.

Результаты представлены в таблице.

Поставщики	Мощности поставщиков	Потребители и их спрос
		1	2	3	4
		50	50	40	60
1	30	5	4	6	4
2	70	4	5	5	8
3	70	7	3	4	7
4	70	0	0	0	0

Самостоятельно решите следующие задачи:

5.1. Найти первоначальное базисное распределение поставок методом «северо-западного» угла.

1)

Пункты отправле ния	Пункты назначения				Запасы
	B1	B2	B3	B4
A1 A2 A3 A4	2 5 11 6	4 1 6 5	7 8 4 12	9 12 3 8	200 270 130 200
Потребности	220	180	240	160	800

2)

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1 A2 A3 A4	18 3 4 7	2 4 5 1	3 8 6 5	12 7 12 6	180 160 140 220
Потребности	150	250	120	180	700

3)

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1 A2 A3 A4	18 3 4 7	2 4 5 1	3 8 6 5	12 7 12 6	380 160 240 220
Потребности	350	250	220	180	1000

4)

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1 A2 A3 A4	18 3 4 7	2 4 5 1	3 8 6 5	12 7 12 6	280 160 240 220
Потребности	250	250	220	180	900

5)

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1 A2 A3 A4	18 3 4 7	2 4 5 1	3 8 6 5	12 7 12 6	380 360 140 220
Потребности	150	350	320	280	1100

5.2. Найти первоначальное базисное распределение поставок методом наименьших затрат.

1)

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1 A2 A3 A4	18 3 4 7	2 4 5 1	3 8 6 5	12 7 12 6	180 360 340 220
Потребности	250	350	220	280	1100

2)

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1 A2 A3 A4	8 3 4 7	2 4 15 1	3 6 6 5	12 7 2 6	180 160 40 220
Потребности	150	250	120	80	600

3)

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1 A2 A3 A4	8 3 4 7	2 4 5 10	3 8 16 5	12 7 12 6	180 60 140 120
Потребности	50	150	120	180	500

4)

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1 A2 A3 A4	8 3 4 2	2 4 5 1	3 8 6 5	2 7 12 6	140 60 140 220
Потребности	110	50	120	180	560

5)

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1 A2 A3 A4	18 3 14 7	12 4 5 10	3 8 6 5	12 7 12 6	80 110 140 180
Потребности	100	150	120	160	530

5.3. Выполнить первоначальное распределение поставок по правилу «северо-западного угла» и правилу учета наименьших затрат в следующей задаче. Подсчитать стоимости затрат при этих распределениях поставок.

Исходные данные представлены в таблице. Стоимость перевозок указана в левых верхних углах ячеек.

Запасы поставщиков	Спрос потребителей
	60	70	110
150	6	10	4
90	12	2	8

5.4. Выполнить первоначальное распределение поставок по правилу «северо-западного угла» и правилу учета наименьших затрат в следующей задаче. Подсчитать стоимости затрат при этих распределениях поставок.

Поставщики	Мощности поставщиков	Потребители и их спрос
		1	2	3	4
		60	40	90	60
I	120	4	4	7	5
II	80	2	3	6	8
III	50	5	1	5	9

5.5. Найти двумя способами (метод минимального тарифа и северо-западного угла), первый опорный план транспортной задачи, в которой запасы на трех складах равны 210, 170, 65 ед. продукции, потребности четырех мага­зинов равны 125, 90. 130, 100 ед. продукции, тарифы перевозки в рублях за единицу продукции следующие:

Сравните полученные опорные планы и соответствующие значения це­левой функции.

6. Имеется три пункта поставки однородного груза А₁, А₂ ,А₃ и пять пунктов В₁, В₂, В₃, В₄, В₅ потребления этого груза. На пунктах А₁, А₂ ,А₃ на­ходится груз соответственно в количестве 100 т, 175 т, 225 т. В пункты В₁, В₂, В₃, В₄, В₅ требуется доставить соответственно 100 т, 130 т, 80 т, 190 т и 100 т.Затраты на перевозку одной тонны груза между пунктами поставки и пункта­ми потребления приведены л матрице С (в руб.):

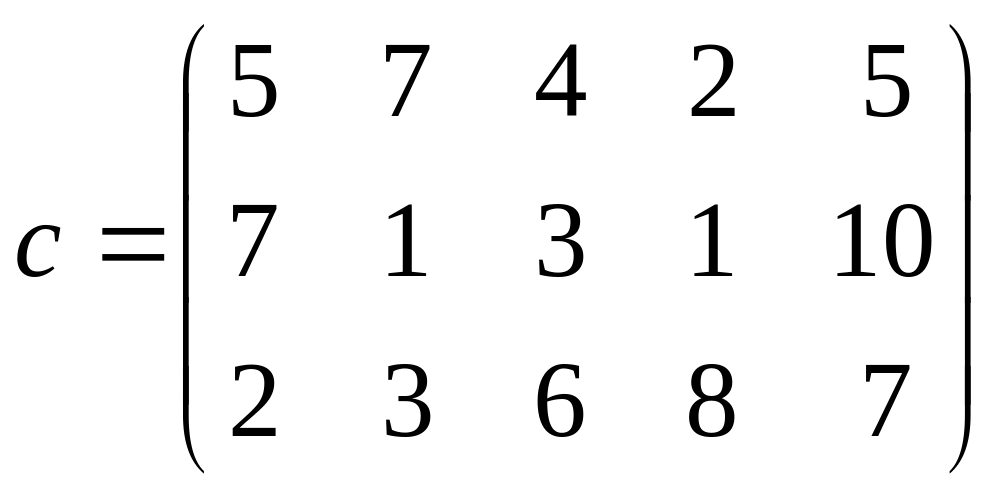
Найдите такой план перевозок, чтобы общие затраты по перевозкам бы­ли минимальными.

5.7. Имеется три поставщика А_i, i=1, 2, 3 с запасами а₁ =30, а₂=70, а₃=70 и четыре потребителя В_j, j=1, 2, 3, 4 с потребностями b₁ =50, b₂ =50, b₃ = 40, b= 60 _. Тарифы перевозок заданы матрицей

Составьте такой план перевозки товара из пункта А_i, в пункт В_j при ко­тором суммарные затраты на перевозку были бы минимальными.

5.8. В транспортной задаче с данным первоначальным распределением поставок построить циклы перераспределения поставок для всех свободных клеток и подсчитать оценки этих циклов.

Поставщики	Мощности поставщиков	Потребители и их спрос
		1	2	3	4	5
		20	80	80	150	150
I	50	7 20	6 30	10	11	12
II	120	10	7 50	9	10	8 70
III	50	4	9	10	7 50	10
IV	260	12	12	7 80	8 100	7 80

5.9. В двух пунктах отправления А и В находится соответственно 150 и 90 т горючего. В пункты 1, 2, 3 требуется доставить соответственно 60, 70 и 110 т горючего. Стоимости перевозки тонны горючего из пункта А в пункты 1, 2, 3 составляют соответственно 6, 10 и 4 ден. ед., а из пункта В – 12, 2 и 8 ден. ед. Составить оптимальный план перевозок горючего так, чтобы общая сумма транспортных расходов была наименьшей.

5.10. На двух складах А и В находится по 90 т горючего. Перевозка одной тонны горючего со склада А в пункты 1, 2, 3 соответственно стоит 1, 3 и 5 ден. ед., а перевозка одной тонны со склада В в те же пункты - соответственно 2, 5 и 4 ден. ед. В каждый пункт надо доставить по одинаковому количеству тонн горючего. Составить такой план перевозки горючего, при котором транспорт­ные расходы будут наименьшими.

5.11. В резерве трех железнодорожных станций А, В и С нахо­дятся соответственно 60, 80 и 100 вагонов. Составить оптимальный план перегона этих вагонов к четырем пунктам погрузки хлеба, если пункту №1 необходимо 40 вагонов, №2- 60 вагонов, №3-­ 80 вагонов и №4- 60 вагонов. Стоимости перегонов одного вагона со станции А в указанные пункты соответственно равны 1, 2, 3, 4 ден. ед., со станции В- 4, 3, 2, 0 ден. ед.и со станции С - 0, 2, 2, 1 ден. ед.

5.12. Завод имеет три цеха А, В, С и четыре склада №1, 2, 3, 4. Цех А производит 30 тыс. шт. изделий, цех В- 40 тыс. шт., цех С- 20 тыс. шт. Пропускная способность складов за то же время характеризуется следующими показателями: склад №1- 20 тыс. шт., склад №2- 30 тыс. шт., склад № 3- 30 тыс. шт., склад № 4- 10 тыс. шт. Стоимости перевозки 1 тыс. шт. изделий из це­ха А в склады № 1, 2, 3, 4 соответственно равны 2, 3, 2, 4 ден. ед.; из цеха В- 3, 2, 5, 1 ден. ед., а из цеха С- 4, 3, 2, б ден. ед. Соста­вить такой план перевозки изделий, при котором расходы на пере­возку 90 тыс. шт. изделий были бы наименьшими.

5.13. На трех складах А, В, С находится сортовое зерно соот­ветственно 10, 15, 25 т, которое надо доставить в четыре пункта: пункту - № 1- 5 т, № 2- 10 т, № 3- 20 т и № 4- 15 т. Стои­мости доставки одной тонны со склада А в указанные пункты соот­ветственно равны 8, 3, 5, 2 ден. ед.; со склада В- 4, 1, 6, 7 ден. ед. и со склада С - 1, 9, 4, 3 ден. ед. Составить оптимальный план пере­возки зерна в четыре пункта, минимизирующий стоимость перевозок.

5.14. Привести открытую транспортную задачу, представленную в таблице, к закрытой.

Поставщики	Мощности поставщиков	Потребители и их спрос
		1	2	3	4
		14	26	7	13
1	95	2	4	3	5
2	35	3	5	7	6
3	55	1	8	4	5
4	75	4	3	2	8

5.15.Привести открытую транспортную задачу, представленную в таблице, к закрытой.

Поставщики	Мощности поставщиков	Потребители и их спрос
		1	2	3	4
		15	25	8	12
1	25	2	4	3	5
2	18	3	5	7	6
3	12	1	8	4	5
4	15	4	3	2	8

5.16. Привести открытую транспортную задачу, представленную в таблице, к закрытой.

Поставщики	Мощности поставщиков	Потребители и их спрос
		1	2	3	4
		50	10	20	50
1	30	5	6	1	2
2	50	3	1	5	2
3	20	8	4	2	5
4	20	6	5	2	4

5.17. Привести открытую транспортную задачу, представленную в таблице, к закрытой.

Поставщики	Мощности поставщиков	Потребители и их спрос
		1	2	3
		100	30	40
1	25	5	4	9
2	2	6	3	4
3	65	3	2	5
4	10	4	2	3