2.2.3. Пример оценки погрешности прямых измерений.

Пример 1. 1)Выбрать вольтметр для проведения измерений. 2)Правильно представить результаты измерения в виде

Даже выбор вольтметра требует метрологического расчета.

Сведения об источнике напряжения:

В наличии 5 вольтметров.

1) 7390А; ; - отпадает по двум причинам:

а)диапазон измерений от 5 В;

б)рассчитан на 50 Гц.

2)Д 5015; ; 7,5;15;30;60 B; 45-1000-2000 Гц

Тоже отпадает по тем же двум причинам.

3)Ц4311; ;от 0,75 до 750 В

от 0,75 до 7,5 45-55-16000 Гц

Подходит по диапазону измерений и по частотному диапазону, но

- отпадает по входному сопротивлению.

4)В3-39; ; от 1 мВ до 300 В, есть 1 В;

20-45 Гц – 1 МГц – 10 МГц

Подходит по диапазону измерений и по частотному диапазону.

- подходит по входному импедансу. Основная погрешность: от 3 мВ до 1 В;

5)В7-26; ; наот 1 до 300 В

на низкочастотном входе от 20 Гц до 20 кГц

на низкочастотном входе.

Тоже подходит по диапазону измерения, частотному диапазону и входному импедансу.

Основная погрешность: на низкочастотном входе.

Вывод:в принципе подходят и В3-39, и В7-26;для выбора наиболее подходящего необходимо сделать метрологический расчет ожидаемой погрешности измерения.

Итак:и.

В3-39 лучше по , но у него больше, которая влияет на. Поэтому без расчета выбрать нельзя.

Основная погрешность:

Для обоих вольтметров

для В3-39

для В7-26

Следовательно, для В3-39

для В7-26

Погрешность от взаимодействия для В3-39 была вычислена:

Абсолютная , но не знаемU. При небольшомU=1 B

.

Таким образом, .

Тем более это справедливо для В7-26, т.к. у него меньше , и , следовательно, меньше, но больше.

Производим измерение U=0.66В.

Теперь уточняем :

Следовательно:

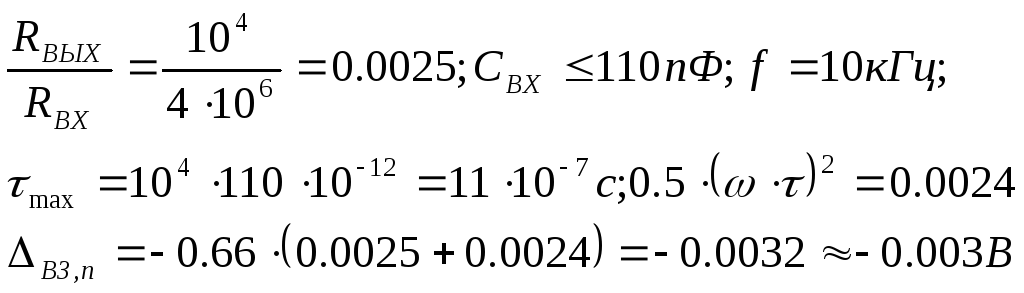
Рассчитаем предельные значения погрешности измерения при арифметическом суммировании. Пределы погрешности измерения несимметричны:

Различие невелико, с небольшим превышением можно принять и тогда

Р=1- можно не писать, а, тогда, по умолчанию, это говорит о том, что Р=1.

Итак: .

Пример 2:

Все то же, что и в примере 1, но температура окружающей среды =35С. В этом случае возникает третья составляющая погрешности – дополнительная температурная погрешность;

где К – температурный коэффициент; - нормальное значение.

Предельное значение К:

Пределы погрешности измерения:

Таким образом, в данном случае можем записать .

2.3. Составляющие погрешности косвенных измерений.

При косвенных измерениях сопротивления R

Точная формула для вычисления сопротивления зависит от схемы измерения. Для случая, рассмотренного ранее

В общем случае формулу, по которой производится вычисление при косвенном измерении, можно представить в виде:

гдеи т.д. – результаты прямых измерений.

В нашем примере

Погрешности прямых измерений обозначим . Будем считать, что какие-либо характеристики этих погрешностей, например, их предельные значениянам известны.

Ясно, что - это составляющие погрешности косвенного измерения. Какие еще есть составляющие погрешности?Да, есть еще одна – методическая погрешность, в частности, методическая погрешность от неточности формулы:

Итак:

2.3.2 Суммирование погрешностей прямых измерений при определении

погрешности косвенного измерения.

Рассматриваем вопрос о суммирование ;;…., оставляя пока в стороне методическую составляющую.

Пусть известны предельные значения ;;…., требуется найти предельные значениясуммы этих составляющих.

В общем виде:

Это формула полного дифференциала функции.

Предельные значения

Рассмотрим два важных частных случая

здесь, следовательно

Например, при имеем

таким образом здесь суммируются модули пределов абсолютной погрешности.

Заметим, что для

Следовательно , так, что приимеем.

Но мы не знаем и, а знаеми, которые имеют знаки «+» и «-», поэтому в худшем случае.

2) , где показатели k,l…m – любые действительные числа, положительные и отрицательные, целые и дробные. Определим частные производные:

Это можно записать в виде

,

т.е.

k=1; l=-1

следовательно

;

или, в обозначениях примера

.

Если k=l=…=m=1, т.е., то

то же самое будет и в случае

, т.е. когдаk=l=…=p=1: q=r=…=n=1

Таким образом здесь суммируются матрицы относительных погрешностей.

Особый случай: Некоторые или все измеряются одним и тем же прибором - иногда при этом происходит частичная компенсация погрешностей прямых измерений.

Ограничимся и рассмотрим два варианта функции:

1) ; 2)

и будем считать, что измеряется одним прибором, аи- другим (одна и та же физ. величина).

В этих случаях:

1) ; 2)

Совершенно очевидно, что в частном случае, при погрешностииилиивзаимно уничтожаются, а функция вырождается в.

А если ?

Можно ли утверждать, как раньше, что:

1) 2)?

Это означало бы, что один и тот же прибор при измерении дает(или), а при измерении(или).

Может ли такое быть?

Вопрос этот не простой. Чтобы его решить, нам надо ввести еще одно подразделение погрешностей средств измерения – по критерию зависимости значений погрешности от значений измеряемой величины.

Возможны следующие варианты:

В реальном СИ обычно есть все три варианта.

Объяснение названий “аддитивная” и “мультипликативная”:

добавление постоянной величины(add);

умножение на постоянную величину

(multiply)

Возвращаемся к нашим примерам. Если бы прибор, измеряющий иобладал только аддитивной погрешностью, то в случае 1) произошла бы полная компенсация:, а в случае 2) – частичная компенсация:- которая пристремилась бы к полной компенсации.

Если же этот прибор обладал бы только мультипликативной погрешностью, полная компенсация была бы в случае 2):, а в случае 1) – частичная компенсация:, которая пристремилась бы к полной.

Но обычно, как уже говорилось, реальная СИ содержит все три составляющие и нормируется общая погрешность, без раздельного нормирования.

Однако, в некоторых случаях указанные составляющие нормируются отдельно. Пример – электронно- лучевой осциллограф (С1-76;в л. р. №6).

Если известны не , а, то –статистическое суммированиепогрешностей прямых измерений при определении погрешности косвенного измерения:

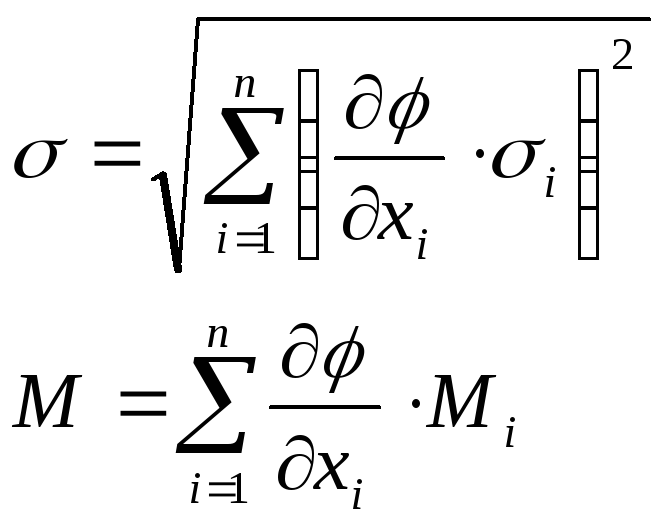
2.3.3. Примеры оценки погрешности косвенных измерений.

Пример 1:

Измерение сопротивления.

Схема из раздела 1.5., которая используется в л.р. №5:

Результаты прямых измерений:

Сопротивление вольтметра: . Требуется записать результат косвенного измеренияR.

.

Вычислим предельные значения относительных погрешностей результатов прямых измерений:

Можно доказать, что при методическая погрешность от неточности формулы, по которой вычисляется значениеR, определяется выражением

(просил вывести её самостоятельно, когда читал раздел)

Подставляя вычисленное значение Rи номинальное значение, получим:

.

Соответственно

Эта погрешность систематическая, и её можно исключить, введя поправку в результат.

Тогда останется погрешность, обусловленная отклонениями от номинала:

Однако ясно, что относительное значение этой погрешности будет порядка , т.е. оно ничтожно мало по сравнению си.

Поэтому погрешность измерения будет содержать только 2 составляющие:погрешности прямых измерений напряжения и тока;её предел:

.

После округления с учетом поправки получим:

Тогда

Пример 2.

Выполнение п.6 задания л.р. №1 (в измененной редакции), считая, что значение скважности импульсов напряжения на зажимах 3-3 составляет

Напомним, что в описании л.р. п.6 сформулирован так:“Выбрать вольтметры и произвести измерение среднего и среднеквадратического значений периодического напряжения на зажимах 3-3, представляющего собой положительные импульсы прямоугольной формы”.

Ориентировочные данные о напряжении на зажимах 3-3, приведенные на лабораторном стенде:

Среднее значение этого напряженияможно измерить вольтметром Ц4311 или В7-26 в режиме измерения напряжения постоянного тока.

Почему?

Известно, что из всех измерительных механизмов только один пригоден для измерения среднего значения – магнитоэлектрический. Среди имеющихся на стенде вольтметров Ц4311, при измерении напряжения постоянного тока как раз и является магнитоэлектрическим

вольтметром ( а при измерении sin – выпрямительным ). В принципе его можно было

бы использовать, но при этом будет получаться большая погрешность от взаимодействия, ибо у него не очень велико.

Какое у него ?

Это зависит от диапазона измерения. На каком диапазоне мы будем работать?Для этого надо ориентировочно представлять себе значение.

где - скважность.

В дополнительной информации на стенде указано С=1,5.

Тогда .

Поскольку дано ориентировочно, возможны диапазоны с верхним пределом либо 30 В, либо 100 В. Ток полного отклонения на обоих пределах составляет 3 мА.

Значит, на пределе 30 В и33 кОм на пределе 100 В.

При это соответствует большой погрешности(можно не считать). Вместе с тем, есть В7-26, который в режиме измерения напряжения постоянного тока имеет структуру:

; в целом

Усилитель принципиально ничего не изменяет, значит, этот вольтметр тоже реагирует на . Но у него. Следовательно

.

Поскольку % погрешностью от взаимодействия можно пренебречь.

Итак, для измерения подходит В7-26. Среднеквадратичное значениеUможно будет измерить электростатическим вольтметром – он имеет очень широкий частотный диапазон и очень большое.

можно измерить, ноU– не измерить, а вычислить, зная скважность.

, и применяя для напряжения со скважностью С

Таким образом

Отсюда

При заданной скважности, например, С=1,5, измерение вольтметром В7-26 получено:

(на пределе 100 В)

Поскольку условия принимаются нормальными и погрешностью от взаимодействия можно пренебречь, имеем

Следовательно,

При выполнении дополнительных метрологических расчетов дается, что

Тогда , т.е.k=1; l=0,5

Здесь - предел относительной погрешности измерения - предел относительной погрешности измерения скважности С.

Здесь может возникнуть сомнение:мы измеряем и поэтому 7,3% - это предел относительной погрешности прямого измерения, но С мы не измеряем, так можем говорить о косвенном измерении.

Можем. Если мы имеем заданную скважность в виде , это значит, сто её измерили.

Теперь можем найти предел абсолютной погрешности косвенного измерения U.

Результат:.

Таким образом, вместо при С=1,5 имеемпри

Пример 3.

Потенциометры постоянного тока.

Потенциометр – прибор для измерения напряжения, обычно значительно более точный, чем вольтметр. Потенциометр постоянного тока измеряет напряжение постоянного тока. Но, применяя косвенное напряжение, потенциометром можно определить и другие физические величины– ток, сопротивление.

С помощью потенциометра измерить неизвестное сопротивление (но и должным образом представить результат измерения.)

Схема эксперимента:

- образцовый резистор.

Здесь мы имеем особый случай косвенного измерения, когда иизмеряются одним и тем же прибором – потенциометром.

В применявшихся ранее обозначениях

Здесь - относительная погрешность образцового резистора

- относительные погрешности измеренияипотенциометром.

Здесь проявляется эффект частичной компенсации. Чтобы понять, нужно знать принцип действия потенциометра и особенности нормирования его точности.

Измерение любого напряжения Uпотенциометром происходит в два этапа: сначала по нормальному элементу с ЭДСустанавливается т.н. рабочий токI;когда он установлен, справедливо равенство

,

где - сопротивление, на котором создается падение напряжения, сравнимое с, затем производится собственно измерениеU- оно сравнивается с компенсирующим напряжением.

по достижении .

Отсюда – главная формула потенциометра

В соответствии с этой формулой относительную погрешность в потенциометре можно представить в виде:

где - погрешность отношения

Сейчас для нас существенно, что не зависит от значенияU, а- зависит, ибозависит отU.

Особенность нормирования точности потенциометров состоит в том, что нормируется только без, т.е. без учета нормального элемента.

Однако, в нашем случае эффект частичной компенсации погрешностей прямых измерений.

икак раз и проявляется в том, чтоисключается.

Предельное значение погрешности нормируется в форме

Класс точности потенциометра c/d.

Подставляя инаходим предельные значения разности

Учитывая, что- это погрешность резистора, т.е., окончательно получим:

Эта формула дает нам предел относительной погрешности косвенного измерения потенциометром классаC/dс использованием образцового резистора классав нормальных условиях.

Пусть потенциометром типа Р309 класс 0,005/0,00025 в нормальных условиях.

Получены значения:

при использовании класс 0,01.

Конечное значение .

Требуется записать результат измерения. С использованием 10разрядного калькулятора получим:

.

Рассчитаем :

Теперь:

точные измерения

Результат: