2.2.1.Составляющие погрешности измерения.

Будем считать, что мы располагаем существующими НМХ.

Покажем составляющие погрешности на рисунке:

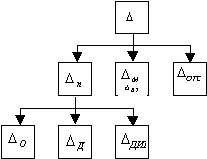
U – инструментальная; М – методическая;вз – взаимодействия СИ с объектом;отс – отсчитывания; О – основная;д – дополнительн(ые);дин – динамическая.

В частных случаях отдельные составляющие могут отсутствовать:

-в ЦИП – отсутствует ;

-при статистических измерениях отсутствует.

Если, кроме того, ничтожно мала , то мы имеем в простейшем случае:

.

Класс точности СИ дает нам информацию о пределах допускаемых значений и, т.е. дает значенияи.

остановимся подробнее на .

Она возникает в тех случаях, когда информативный параметр входного сигнала Х изменяется во времени:

Х=x(t)=var

Речь идет об измерении линованных значений информативного параметра. Например, в регистрирующих измерительных приборах.

Пример:

измеряется - действующее значение.

Оно, само по себе, во времени не изменяется и является информативным параметром входного сигнала. Таким образом, в данном случае имеем статическое измерение .

Здесь надо сделать оговорку: U=constпо крайней мере за время измерения, а не вообще всегда. Понятия«статика» и «динамика» условны: «статика» - это неизменность хотя бы за время измерения.

Но если то же самое напряжение

подадим на электронно-лучевой осциллограф и видим его на экране,

то можно, пользуясь сеткой на экране и известным масштабом измерить любое мгновенное значение U(t)этого напряжения. В этом случае мы имеем дело с динамическим измерением и.

Правда, измерять мгновенное значение синусоидального напряжения нет смысла, ибо синус – известная функция. Но при более сложной форме кривой это имеет полный смысл:

Обычный вольтметр не дает нам желаемого значения. например. вольтметр. реагирующий на среднее квадратическое значение. дает нам

Вместе с тем у синусоидального напряжения за длительное время может изменяться амплитуда, а значит и среднее квадратическое значение:

t

U(t)=var

Оно может быть зарегистрировано на бумажной ленте регистрирующего прибора. В этом случае измерение является динамическим по отношению к Uи .

Динамические погрешности иного рода – от изменения во времени влияющих величин , - будем относить к числу дополнительных погрешностей .

Так, например, частота нашего напряжения , у которого измеряется , - это не информативный параметр входного сигнала U(t)и погрешность от изменений. f=var– частотная погрешность – относится к числу .

Теперь остановимся на методической погрешности . Для прямых измерений наиболее важным является погрешность от взаимодействия СИ с объектом: , т.е. большей частью можно считать

=

Погрешность от взаимодействия была рассмотрена на примере измерения напряжения постоянного тока наUвольтметром. Показано. что:

где – напряжение Uпосле подключенияV, до подключения было.

R – выходное сопротивление объекта

-входное сопротивление вольтметра.

Опуская индекс «2», ибоUнам никогда не известно, запишем

где U –напряжение, измеренное вольтметром.

Или

А если напряжение синусоидальное?

Входной импеданс вольтметра можно представить параллельным соединением . Выходной импеданс источника сигнала может быть различным. Примем. для простоты. что выходной импеданс чисто активный. Тогда

До подключения U:

После подключения U:

Проверка:

;

;

При иможно воспользоваться свойствами малых величин.

например

Т.о. на переменном токе добавляется слагаемое , где

Пример:

Возьмем вольтметр ВЗ-39. Рассчитан на измерение синусоидальных напряжений в диапазоне частот от 20 Гц до 5 МГц. Его входной импеданс

С помощью вольтметра измеряем напряжение с частотой

f=10 кГц Выходное сопротивление источника .

В данном случае имеем

На частоте f=10 кГц

Если частота этого же источника повысится до 100 кГц, то при прочих равных условиях , т.е. погрешность – порядка 20%.

В этом случае используют другой прибор – вольтметр В7- 26 имеет так называемый высокочастотный и низкочастотный входы.

Высокочастотный вход – это когда измеряемое напряжение подается на «пробник», внутри которого находится амплитудный детектор.

Высокочастотный вход Низкочастотный вход

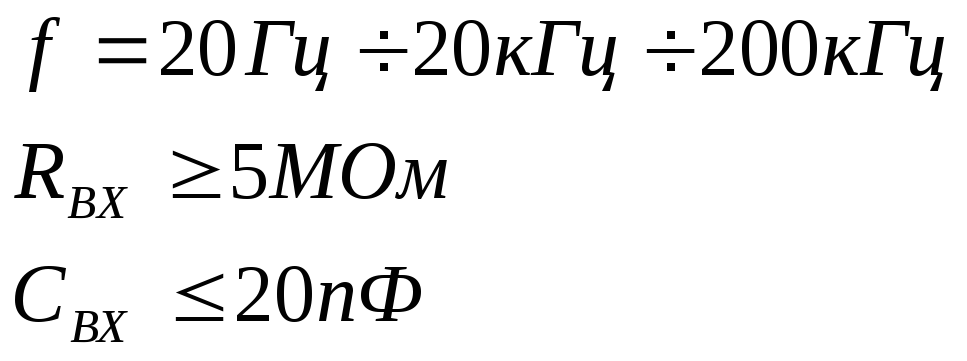
Для низкочастотного входа на частоте 100 кГц (для нашего примера):

Если использовать для измерения одного и того же напряжения оба типа упоминавшихся вольтметров, то показания могут отличаться до 2 раз.

Приведем пример неправильного расчета.

;

Но мы знаем, что. Нельзя формулу расчета погрешности, справедливую на постоянном токе, распространять на синусоидальный.

2.2.2. Суммирование составляющих погрешности измерения.

Как суммировать составляющие?

Если бы погрешности были величинами не случайными (детерминированными), то вопрос бы не возникал – алгебраически сложить и все.

Но погрешности имеют случайную природу.

При этом имеем в виду. что есть систематические и случайные составляющие, и не только это. Допустим. что речь идет об основной погрешности и можно считать, что случайной составляющей можно пренебречь, т.е . Все равно для каждого данного экземпляра СИ значение случайно. Допустим, речь идет о дополнительной температурной погрешности. Допустим также, что мы точно знаем, какая сейчас температура в помещении, где выполняется измерение. Все равно дополнительная температурная погрешность не может быть найдена как детерминированная величина. а лишь как случайная, ибо температупный коэффициент для данного экземпляра СИ нам не известен. Мы знаем лишь пределы основной погрешности, дополнительных погрешностей для совокупности СИ данного –типа.

Если мы тем или иным способом узнали погрешность для данного экземпляра СИ, то можно внести поправку и исключить ее. Поэтому детерминированноя погрешность – это уже не погрешность. Итак. погрешности – случайные величины. Но как суммировать случайные величины?Это зависит от того, что нам о них известно.

Если мы знаем только пределы возможных значений случайных величин, то единственное, что мы можем сделать – суммировать эти пределы:

После этого результат измерения можно представить в виде:

Такая форма годится для случая, когда пределы всех составляющих двузначны и симметричны относительно нуля:

Если же некоторые несимметричны, т.е:

то необходимо отдельно вычислить нижний и верхний пределы погрешностей измерения:

где – номера составляющих с несимметричными пределами; - с симметричными.

После этого результат измерения можно представить в виде:

от доP=1

Если мы знаем только пределы составляющих, то, строго говоря, больше ничего сделать нельзя.

Однако, желательно знать больше. Почему?

Потому, что арифметическое суммирование пределов составляющих дает завышенные погрешности измерения. Пусть имеются только две составляющих: ис пределамии.

Как , так имогут принимать любые значения и, в частности, крайние, например. Однако, интуитивно ясно, что маловероятно, чтобы обе оказались на краю, т.е. значение погрешности измерениявозможно, но маловероятно.

Напомним. что по ГОСТ 8.009-84 арифметическое суммирование соответствует второй модели погрешности. Эта модель. допустима, но рекомендуется ее применять лишь в особо ответственных случаях. Между тем, существующая НМХ, строго говоря. только ее и позволяет применять. Если применить более реальное суммирование – статистическое, то нам неизбежно приходится принимать какие-либо допущения, говорить: » Допустим, что..."

И что значит «статистическое суммирование»?

Чтобы ответить на эти вопросы необходимо из теории вероятности привлечь понятия:

-закон распределения случайной величины;

-математическое ожидание случайной величины;

-дисперсия и СКО случайной величины;

-зависимые и независимые случайные величины;

- как суммировать МО случайной величины;

- как суммировать СКО независимых случайных величин.

Обозначим случайную величину А, у нас это либо составляющие , либо результирующая погрешность измерения.

Исчерпывающей характеристикой любой случайной величины А является закон ее распределения. Он может быть выражен в двух формах:интегральной и дифференциальной. Интегральный закон распределения случайной величины А или интегральная функция распределения – это

F(a)=p(A<a),

где р – вероятность;а – текущая переменная.

Чаще пользуются дифференциальной функцией распределения;ее называют также плотностью распределения или плотностью вероятности:

Разные виды f(a), например, для закона равномерной плотности:

Для погрешностей особенно важное значение имеет нормальный закон распределения или закон Гаусса. Для него f(a) имеет вид колокола.

Обычно используется не F(a) илиf(a) , а числовые характеристика закона распределения. Среди них – математическое ожидание и дисперсия случайной величины.

МО - это:

Обычно законы распределения погрешностей симметричны относительно МО.

Центрированная случайная величина - это:

Если А - случайная величина, а В- неслучайная величина и С=ВА, то М(С)=ВМ(А);М(В)=В.

Дисперсия - это:

Удобнее пользоваться средним квадратическим отклонением случайной величины, которое имеет ту же размерность, что и сама случайная величина:

Dихарактеризуют степень разбросанности случайной величины вокруг М:

Если А - случайная, а В - неслучайная величины и С=ВА, то .

Нормальный закон:

Вероятность:

N=K;зависимость Р от К табулирована.

К	1	2	3	4	5
Р	0,6827	0,9973	0,9973	0,99994	0,9999994

Усеченный нормальный закон

Перейдем к вопросу о статистическом суммировании. Сначала будем считать, что есть только две случайных величины, и, и в результате их суммирования образуется третья случайная величина А.

В этом случае, для М.О. имеем:

-

М.О. алгебраически суммируются. А дисперсии и СКО?Рассмотрим вопрос о зависимости случайных величин. В теории вероятности зависимость между случайными величинами не жестко детерминирована. В теории вероятности мы встречаемся с более общим типом зависимости- вероятностной зависимостью. Вероятностная зависимость означает, что с изменением одной величины другая изменяется лишь с определенной тенденцией изменяться.

Эта тенденция наблюдается лишь в среднем и в каждом отдельном случае от нее возможны отступления.

Пример:одна величина - рост наугад взятого человека, другая - его вес или масса. Ясно, что в общем, в среднем, зависимость есть и она в том, что более высокие имеют больший вес. Известны даже эмпирические формулы, выражающие эту зависимость, например:

Масса(кг)=рост(см)-100.

В то же время ясно, что это лишь в среднем, а даже для отдельно взятых людей может быть вполне, что высокий легче более низкого.

Для того, чтобы отличать такую вероятностную зависимость от жесткой функциональной зависимости её называют корреляционной зависимостью. Корреляция - это статистическая взаимосвязь между случайными величинами. В нашем примере масса коррелирована с ростом. Степень взаимосвязи отражает коэффициент корреляции. Запишем СКО суммы двух случайных величин:

здесь r- коэффициент корреляции, который может принимать любое значение от -1 до 1;

r>0- положительная корреляция - возрастание

r<0 - отрицательная корреляция- убывание.

Для краткости запишем:

Предельные случаи:r=0- случайные величины независимы

r=1 иr=-1- жесткая функциональная зависимость

В большинстве случаев составляющие погрешности измерения независимы.

Для произвольного числа суммируемых независимых случайных величин.

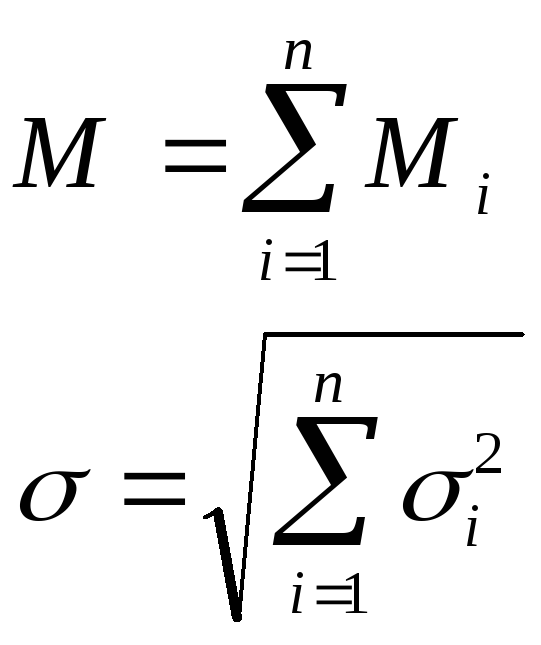
Переходя к погрешностям запишем:

или

Первая формула справедлива всегда, а вторая - в случае, когда составляющие - независимы.

Предполагается, что мы откуда-то знаем и. Но вся беда в том, что существующие НМХ СИ не дают нам сведений об их числовых характеристиках, а дают только пределы. Но все же если мы располагаем статистическими характеристикамии, или будем ими располагать в будущем, то как же нам все-таки представить результат измерения?

М() характеризует смещенность полученного значения Х относительно, поэтому М() целесообразно учесть введением поправки:

или

характеризует разбросвокруг, поэтому нужно указать пределы, внутри которых с некоторой вероятностью Р лежит.

Р илиР

Итак, окончательно:

где

; P

Cвязь К и Р зависит от закона распределения. Но знаем ли мы этот закон?То, что мы знаем все, это еще не значит, что мы знаем законы распределения составляющих.

И тем не менее, как это ни удивительно, в ряде случаев у нас есть основания утверждать,

что мы знаем закон распределения , не зная законов распределения.

В теории вероятности есть т.н. центральная предельная теорема. Смысл её в том, что если мы имеем много случайных величин, они независимы и никакая из них особенно не выделяется, то тогда, какими бы ни были законы распределения этих величин, закон распределения их суммы будет близок к нормальному. Это - великая теорема. и в этом особая роль нормального закона среди других. Качественно это можно продемонстрировать так. Пусть ираспределены по закону равномерной плотности и имеют одинаковые пределы.

Это распределение (равномерное) совсем не похоже на колоколообразное нормальное.

Как будет распределена ?Доказывается, чтобудет распределена по закону треугольника (закон Симпсона):

Этот закон тоже еще далек от“колокола”, но ближе к нему, чем исходный закон равномерной плотности.

При трех составляющих получим функцию,

напоминающую “колокол”.

Итак, в ряде случаев есть основание считать, что результирующий закон близок к нормальному, а для него связь К и Р известна. Вспомним таблицу:если, например, назначить

К=2, то

А если К=3, то

Но все это получено в предположении, что нам известны и.

В действительности же в настоящее время НМХ СИ таковы, что нам известны пределы . Можно ли тогда говорить о статистическом суммировании?Строго говоря, суммирование в этом случае может быть только арифметическим. Но оно невыгодно, т.к. завышает. Поэтому желательно применить статистическое суммирование. И тогда говорят:

“Допустим, что...”(т.е. вынуждены допустить).”Допустим, что все составляющие распределены по нормальному усеченному закону”. Это значит, что, т.е. зная, мы тем самым знаеми можем их статистически суммировать:

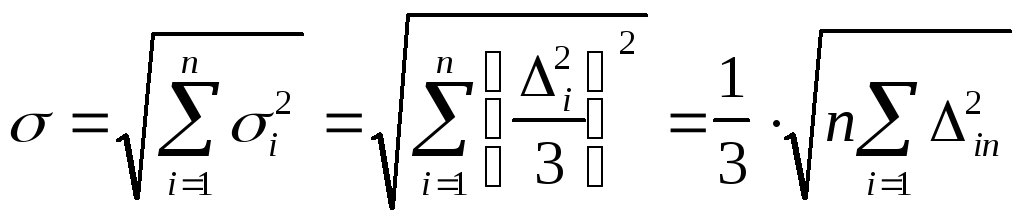
Если бы составляющие были распределены не по усеченному, а просто по нормальному закону, то, как это известно из теории вероятности, закон распределения их суммытоже был бы строго нормальным. Если же мы говорим, чтораспределены по усеченному нормальному закону, то мы вправе считать, что закон распределенияблизок к нормальному (центральная предельная теорема).

Поэтому, мы можем записать:

где К и Р связаны зависимостью, которая уже нам известна для нормального закона.

В частном случае, если назначить Р=0,997, то К=3 и тогда

.

Теперь можем оценить эффект, который в самом благоприятном случае нам может дать статистическое суммирование по сравнению с арифметическим.

При арифметическом:

В каком случае будет наибольший выигрыш?

Допустим, что какая-то одна составляющая сильно преобладает над остальными. Тогда

и

и ,

как при статистическом, так и при арифметическом суммировании, т.е. здесь нет различия.

Максимальный выигрыш, очевидно, будет в том случае, когда все составляющие равны. Тогда

При статистическом суммировании получаем и враз меньше, чем при арифметическом.

Если, например, n=9, то выигрыш в 3 раза, между тем, как вероятности составляют 0,997 и 1.

При малом числе составляющих, когда их 2-3 выигрыш несущественный;В лучшем случае вираз.

Таким образом, если имеем дело с суммированием двух или трех составляющих погрешности, возможно проводить суммирование арифметически. Выигрыш от статистического суммирования невелик, но требует допущений о законах распределения этих составляющих.