
- •630092, Г. Новосибирск, пр. К. Маркса, 20
- •Оглавление
- •Предисловие
- •1. НадежносТь элемента и системы, эксплуатируемой до первого отказа Типовые задачи с решениями
- •Решение
- •Решение
- •Задачи для самостоятельного решения по разделу 1 Задание 1
- •Схемы электроснабжения потребителей
- •2. Надежность системы с зависимыми элементами Типовые задачи с решениями
- •Решение
- •Решение
- •Задачи для самостоятельного решения по разделу 2 Задание 2
- •3. Надежность восстанавливаемого элемента Типовые задачи с решениями
- •3.1. Время восстановления элемента пренебрежимо мало
- •Решение
- •Решение
- •3.2. Время восстановления элемента соизмеримо со временем его эксплуатации до отказа
- •Решение
- •Задачи для самостоятельного решения по разделу 3 Задание 3
- •4. Резервирование в технических системах Типовая задача с решением
- •Решение
- •Задача для самостоятельного решения по разделу 4
- •5. Законы распределения сроков службы стареющих элементов Типовые задачи с решениями
- •5.1. Усеченный нормальный закон
- •Решение
- •5.2. Комбинированный закон
- •Задачи для самостоятельного решения по разделу 5 Задание 5
- •6. Предупредительные замены стареющих элементов Типовая задача с решением
- •Решение
- •Задачи для самостоятельного решения по разделу 6 Задание 6
- •Библиографический список
4. Резервирование в технических системах Типовая задача с решением
Резервирование является одним из способов повышения надежности технических систем. Обычно рассматриваются следующие виды резерва:
нагруженный или горячий резерв;
ненагруженный или холодный резерв;
облегченный резерв.
Возможная схема эксплуатации системы с резервированием показана на рис. 4.1. Каждый отказавший элемент поступает в ремонтное устройство, содержащее r ремонтных единиц, любая из которых может восстанавливать один элемент. Если все ремонтные места заняты, то элемент ставится в очередь. Система эксплуатируется исправно, если число рабочих элементов не меньше j (j £ n).


Рис. 4.1. Схема эксплуатации системы с резервированием
Вероятность того, что система находится в состоянии k (в системе отказало k элементов), определяется как
pk
= где k
= 1...(N
– j).
(4.1)
где k
= 1...(N
– j).
(4.1)
Входящая в выражение (4.1) вероятность р0 определяется следующим образом:
 ,
,
 (4.2)
(4.2)
Интенсивности отказа и восстановления системы, находящейся в k-м состоянии, определяются по выражениям:
 (4.3)
(4.3)
 (4.4)
(4.4)
В
системе эксплуатируются 4 рабочих
элемента (n
= 4), 2 элемента,
находящихся в горячем резерве (m
= 2), и 1 элемент
– в облегченном резерве
 (ненагруженный резерв отсутствует).
Интенсивности отказов элементов,
находящихся в рабочем режиме и в режиме
нагруженного горячего резерва, составляют
l
= 0.50 1/ч, в режиме облегченного резерва
(ненагруженный резерв отсутствует).
Интенсивности отказов элементов,
находящихся в рабочем режиме и в режиме
нагруженного горячего резерва, составляют
l
= 0.50 1/ч, в режиме облегченного резерва
 =
0.25 1/ч. Число ремонтных единиц
r
= 2. Интенсивность
потока восстановления m
= 1 1/ч. Определить вероятность эксплуатации
системы при k
отказавших элементах, математическое
ожидание числа отказавших элементов,
а также вероятность сохранения
работоспособности системы (система
выполняет свои функции, если в ней
эксплуатируется не менее 3 рабочих
элементов). Сравнить полученные результаты
с результатами в системе, содержащей 4
ремонтные единицы (r
= 4).
=
0.25 1/ч. Число ремонтных единиц
r
= 2. Интенсивность
потока восстановления m
= 1 1/ч. Определить вероятность эксплуатации
системы при k
отказавших элементах, математическое
ожидание числа отказавших элементов,
а также вероятность сохранения
работоспособности системы (система
выполняет свои функции, если в ней
эксплуатируется не менее 3 рабочих
элементов). Сравнить полученные результаты
с результатами в системе, содержащей 4
ремонтные единицы (r
= 4).
Решение
Интенсивности
потоков отказов системы, находящейся
в k-м
состоянии, будут: l0
= (4 + 2)l
+
=
3.25 1 1/ч,
 В случае 2
ремонтных единиц интенсивности потоков
восстановления системы, находящейся в
k-м
состоянии, определятся как
В случае 2
ремонтных единиц интенсивности потоков
восстановления системы, находящейся в
k-м
состоянии, определятся как
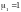 1/ч,
mk
= 2m
(k
= 2...7).
1/ч,
mk
= 2m
(k
= 2...7).
Вероятности
эксплуатации системы при k
отказавших элементах согласно (4.1) и
(4.2) будут: р0
= 3.41647·10–2,
р1
= 1.1088158·10–1,
р2
=
= 1.6632238·10–1,
р3
= р4
= 2.0790297·10–1,
р5
= 1.5592723·10–1,
р6
=
= 7.79963514·10–2,
р7
= 3.8901808·10–2.
Математическое ожидание числа отказавших
элементов составляет М[k]
= = 3.419. Вероятность сохранения
работоспособности системы отвечает
эксплуатации не менее 3 элементов: Р
= р0
+ р1
+ р2
+ р3
+ р4
= 0.727.
= 3.419. Вероятность сохранения
работоспособности системы отвечает
эксплуатации не менее 3 элементов: Р
= р0
+ р1
+ р2
+ р3
+ р4
= 0.727.
В
случае, если число ремонтных единиц
составляет r
= 4, интенсивности
потоков восстановления будут:
 (k
= 1...4), m5
= 4!·4,
m6
= 4!·42,
m7
= 4!·43.
При этом вероятности рk
определятся как: р0
=
=
0.0640504, р1
= 2.0816367·10–1,
р2
= 3.122455·10–1,
р3
= 2.6020459·10–1,
р4
= 1.3010229·10–1,
р5
= 9.9871956·10–3,
р6
= 1.219709·10–2,
р7
=
= 3.0492725·10–3.
При этих значениях вероятностей pk
M[k]
= 2.278, P
=
=
p0
+ p1
+ p2
+ p3
+ p4
= 0.975.
(k
= 1...4), m5
= 4!·4,
m6
= 4!·42,
m7
= 4!·43.
При этом вероятности рk
определятся как: р0
=
=
0.0640504, р1
= 2.0816367·10–1,
р2
= 3.122455·10–1,
р3
= 2.6020459·10–1,
р4
= 1.3010229·10–1,
р5
= 9.9871956·10–3,
р6
= 1.219709·10–2,
р7
=
= 3.0492725·10–3.
При этих значениях вероятностей pk
M[k]
= 2.278, P
=
=
p0
+ p1
+ p2
+ p3
+ p4
= 0.975.
Таким образом, увеличение числа ремонтных единиц с двух до четырех привело к уменьшению математического ожидания числа отказавших элементов с 3.419 до 2.278 и к увеличению вероятности сохранения работоспособности системы с 0.727 до 0.975.
