
- •Содержание
- •Введение
- •1. Оценки истинного значения измеряемой величины
- •1.1. Понятие о типах оценок и их свойствах
- •1.2. Точечные оценки
- •1.3. Доверительные оценки при равноточных измерениях
- •2. Метод наименьших квадратов (мнк)
- •3. Численное интегрирование
- •4. Задания контрольной работы
- •Контрольные вопросы
- •Литература
3. Численное интегрирование
Правило трапеций, оценка ошибки
Правило трапеций обычно применяют в том случае, когда значения функции измерены для равноотстоящих значений аргумента, т.е. представлены таблицей с постоянным шагом h:
х |
у=f(х) |
х0=а |
у0 |
х1=х0+h |
у1 |
х2=х1+h |
у2 |
… |
… |
хn=в=хn-1+h |
уn |
По правилу трапеций в качестве приближенного значения интеграла
![]() (1)
(1)
принимают величину
![]() , (2)
, (2)
т.е.
полагают
![]() .
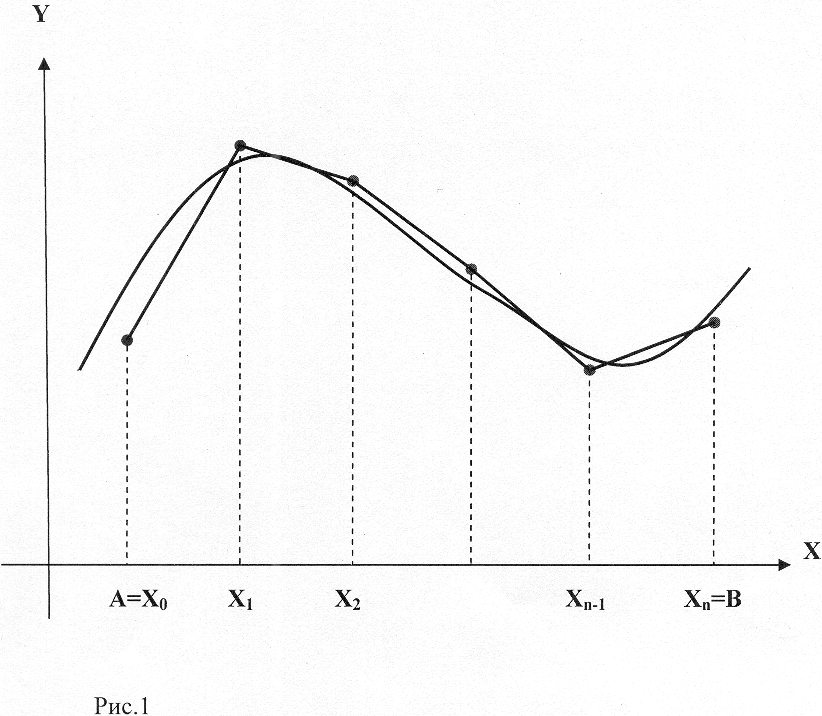
Геометрическая интерпретация правила
трапеций дана на рис. 1: площадь
криволинейной трапеции заменяется
суммой площадей прямолинейных трапеций.
.
Геометрическая интерпретация правила
трапеций дана на рис. 1: площадь
криволинейной трапеции заменяется
суммой площадей прямолинейных трапеций.
При этом, как показано на рис. 1, измеренные значения функции ук могут не совпадать со значениями функции f(x) в точках хк, т.к. измеренные значения функции содержат ошибки эксперимента.
Полная ошибка вычисления интеграла по правилу трапеций оценивается как сумма двух ошибок: ошибки усечения (аналитической ошибки), вызванной заменой криволинейной трапеции прямолинейными, и ошибки округления (эмпирической ошибки), вызванной ошибками измерения значений функции.
а) Ошибка усечения оценивается в зависимости от степени гладкости функции f(x) следующим образом.
1) Для функции у= f(x), непрерывной на отрезке [a, b],
![]() ,
,
что обеспечивает вычисление интеграла с любой наперед заданной точностью при достаточно малом шаге h.
2) Для
функции у= f(x)
с непрерывной производной второго
порядка
![]() на отрезке [a, b]
на отрезке [a, b]
![]() ,
(3)
,
(3)
где с – некоторая точка интервала (a, b) или
![]() , (4)
, (4)
где
![]() ,
о(h2) есть малая более
высокого порядка, чем h2,
при
,
о(h2) есть малая более
высокого порядка, чем h2,
при
![]()
Приближенно оценка ошибки усечения дается формулой
![]() (5)
(5)
где Т2h – величина той же структуры, что и Тh, но с двойным шагом 2h (для возможности такой оценки число интервалов n надо брать четным).
![]() б)
Ошибка округления оценивается следующим
образом. В предположении, что измерения
всех значений функции ук произведены
независимо друг от друга с одинаковой
точностью, а именно со средней
квадратической ошибкой G,
средняя квадратическая ошибка величины
Тh составляет
б)
Ошибка округления оценивается следующим
образом. В предположении, что измерения
всех значений функции ук произведены
независимо друг от друга с одинаковой
точностью, а именно со средней
квадратической ошибкой G,
средняя квадратическая ошибка величины
Тh составляет
![]() .
. Если ошибки измерения более или менее
точно следуют нормальному закону
распределения (с центром 0 и дисперсией
G2), то по правилу
трех сигм принято считать, что ошибки
округления не превосходит величины
3(b-a)
.
. Если ошибки измерения более или менее
точно следуют нормальному закону
распределения (с центром 0 и дисперсией
G2), то по правилу
трех сигм принято считать, что ошибки
округления не превосходит величины
3(b-a)![]() (надежность этого вывода можно считать
достаточной при достаточно больших n).
(надежность этого вывода можно считать
достаточной при достаточно больших n).
Пример
3.1. Вычислить определенный интеграл
![]() с использованием формулы трапеций при
n=5 и n=10. Для
n=10 оценить ошибку как
сумму двух ошибок: ошибки усечения
и ошибки округления.
с использованием формулы трапеций при
n=5 и n=10. Для
n=10 оценить ошибку как
сумму двух ошибок: ошибки усечения
и ошибки округления.
Решение.
Т.к. при n=5,
![]() ;
а при n=10,
;
а при n=10,
![]() ,
поэтому вычислим значения подынтегральной
функции
,
поэтому вычислим значения подынтегральной
функции
![]() в точках а=х0=1, хк=х0+кh=1+0,1•к,
при к=1, 2, …, 10. Результаты внесем в таблицу
в точках а=х0=1, хк=х0+кh=1+0,1•к,
при к=1, 2, …, 10. Результаты внесем в таблицу
х |
1 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
2 |
|
2 |
2,00909 |
2,03333 |
2,06923 |
2,11429 |
2,16667 |
2,22500 |
2,28824 |
2,35556 |
2,42632 |
2,50000 |
ех+1/х |
7,3891 |
7,4565 |
7,6395 |
7,9187 |
8,2837 |
8,7292 |
9,8257 |
9,8556 |
10,5440 |
11,3172 |
12,1825 |
а) n=5; h=0,2 используем формулу (2)
![]()
![]()
б) n=10; h=0,1.
![]()
![]()
Приближенная оценка ошибки усечения по формуле (5)
![]()
Для более точной оценки ошибки усечения по формуле (3)
находим
![]() :
,
:
,
![]() ,
,
![]() .
.
Тогда:
![]() при 1<c<2 можно оценить
сверху
при 1<c<2 можно оценить
сверху
![]() =31,2176.
Следовательно ошибка усечения по формуле
(3)
=31,2176.
Следовательно ошибка усечения по формуле
(3)

Ошибку округления вычисляем по формуле , , где G=0,0001 (значения ук вычислены с точностью 10-4), h=0,1, n=10
![]()
Тогда
общая ошибка
![]() .
.
Т.о. мы имеем, что при n=10
![]() и ошибка вычисления не превосходит
и ошибка вычисления не превосходит
![]() .
.
