§ 37. Сложение взаимно перпендикулярных колебаний
Пусть
частица участвует одновременно в двух
гармонических колебаниях одинаковой
частоты
,
совершающихся во взаимно перпендикулярных
направлениях. Ориентируем по направлениям
этих колебаний координатные оси
и
,
взяв за начало координат положения
равновесия частицы. Выберем начало
отсчета времени так, чтобы начальная
фаза первого колебания была равна нулю.
Тогда уравнения колебаний имеют вид:
(37.1)
где
– разность фаз обоих колебаний. Таким
образом, траектория частицы представлена
в так называемой параметрической форме.
Чтобы
получить уравнение траектории в обычном
виде, т.е. зависимость
,
нужно исключить из уравнений (37.1) параметр
.
Из первого уравнения системы
,
откуда
Теперь развернем во втором уравнении косинус по формуле косинуса суммы. Получим
.
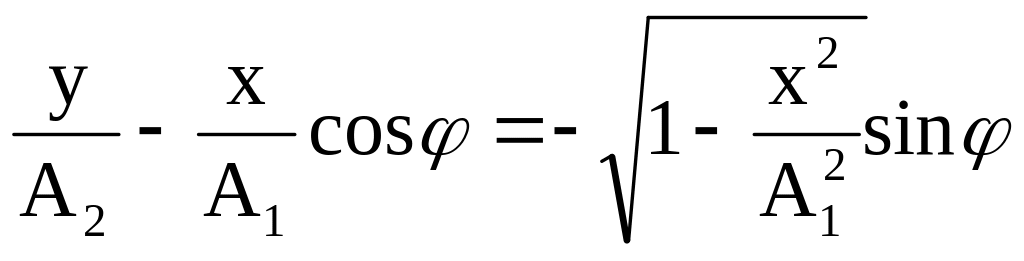Возведем обе части последнего уравнения в квадрат
и приведем полученное выражение к виду
или
В
общем случае разность начальных фаз
колебаний
.
Окончательно уравнение траектории
имеет вид
(37.2)
Из курса аналитической геометрии известно, что уравнение (37.2) представляет собой уравнение эллипса, оси которого произвольно ориентированы относительно осей и . Ориентация эллипса и величины его полуосей зависят довольно сложным образом от амплитуд и разности фаз.
Исследуем форму траектории в частных случаях:
а) разность фаз равна нулю. В этом случае уравнение (37.2) имеет вид
откуда получается уравнение прямой
Следовательно, колеблющаяся частица перемещается по прямой , причем расстояние от нее до начала координат (рис. 37.1)
Рис. 37.1
Подставляя
выражения (37.1) для
и
и учитывая, что
,
получим закон, по которому
меняется со временем:
т.е.
результирующее колебание является
гармоническим вдоль прямой с частотой
и амплитудой, равной
.
б)
разность фаз равна
.
Тогда уравнение (37.2) имеет вид
откуда
получается, что результирующее движение
представляет собой гармоническое
колебание вдоль прямой
(рис. 37.1)
в)
при разности фаз
уравнение (37.2) переходит в
т.е.
в уравнение эллипса, приведенного к
координатным осям, причем полуоси
эллипса равны соответствующим амплитудам
колебаний. При равенстве амплитуд
и
эллипс вырождается в окружность. Случаи
и
отличаются направлением движения по
эллипсу или по окружности (рис. 37.2). Если
,
то уравнения (37.1) можно записать следующим
образом:
Пусть
в момент
частица находится в точке
.
В последующие моменты времени координата
уменьшается, а координата
становится отрицательной. Следовательно,
движение совершается по часовой стрелке.
При
движение совершается против часовой
стрелки.
Рис. 37.2
Таким
образом, равномерное движение по
окружности радиуса
с угловой скоростью
может быть представлено как сумма двух
взаимно перпендикулярных колебаний:
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу. Форма этих фигур зависит от соотношения амплитуд, частот и начальных фаз колебаний.
Вопросы:
1) Какие колебания называются затухающими? вынужденными?
2) Запишите дифференциальное уравнение затухающих колебаний и его решение.
3) По какому закону изменяется амплитуда затухающих колебаний? Являются ли эти колебания периодическими?
4) Дайте определения коэффициента затухания, коэффициента сопротивления, логарифмического декремента затухания. Что показывает логарифмический декремент затухания?
5) Что такое вынуждающая сила?
6) Чему равна частота вынужденных колебаний системы?
7) От чего зависит амплитуда вынужденных колебаний?
8) Какое явление называется резонансом? Приведите примеры резонансных явлений.
9) Какова траектория частицы, участвующей одновременно в двух взаимно перпендикулярных колебаниях с одинаковыми периодами?
Лекция 11. Механические волны