Одноканальная смо с неограниченной очередью

На практике довольно часто встречаются одноканальные СМО с очередью (врач, обслуживающий пациентов, процессор, выполняющий машинные команды). Поэтому необходимо рассмотреть одноканальные СМО с очередью более подробно.

Пусть имеется одноканальная СМО с очередью, на которую не наложено никаких ограничений (ни по длине очереди, ни по времени ожидания). На эту СМО поступает поток заявок с интенсивностью ; поток обслуживаний имеет интенсивность , обратную среднему времени обслуживания заявки t_об. Требуется найти финальные вероятности состояний СМО, а также характеристики ее эффективности:

L_СИСТ – среднее число заявок в систем;

W_СИСТ – среднее время пребывания заявки в системе;

L_ОЧ – среднее число заявок в очереди;

W_ОЧ – среднее время пребывания заявки в очереди;

P_ЗАН — вероятность того, что канал занят (степень загрузки канала).

Что касается абсолютной пропускной способности A и относительной Q, то вычислять их нет необходимости: в силу того, что очередь неограниченна, каждая заявка рано или поздно будет обслужена, поэтому , по той же причине .

Решение. Состояние системы, как и раньше, будем нумеровать по числу заявок, находящихся в СМО:

- S₀ – канал свободен;

- S₁ – канал занят (обслуживает заявку), очереди нет;

- S₂ – канал занят, одна заявка стоит в очереди;

…

- S_k – канал занят, k-1 заявок стоят в очереди.

Теоретически число состояний ничем не ограничено (бесконечно). Формулы для финальных вероятностей в схеме гибели и размножения выводились только для случая конечного числа состояний, но сделаем допущение – воспользуемся ими и для бесконечного числа состояний. Тогда число слагаемых в формуле будет бесконечным. Получим выражение для p_о:

. (17)

Ряд в формуле (17) представляет собой геометрическую прогрессию. Мы знаем, что при ряд сходится – это бесконечно убывающая прогрессия со знаменателем . При ряд расходится (что является косвенным, хотя и не строгим доказательством того, что финальные вероятности состояний p_о, p₁, …, p_k,… существуют только при ). Тогда:

, ,…, (18)

Найдем среднее число заявок в СМО L_СИСТ. Случайная величина Z – число заявок в системе – имеет возможные значения 0, 1, 2, …, k, … с вероятностями p_о, p₁, …, p_k,… Ее математическое ожидание равно:

; (19)

Применяя формулу Литтла (9), найдем среднее время пребывания заявки в системе:

; (20)

Найдем среднее число заявок в очереди. Будем рассуждать так: число заявок в очереди равно числу заявок в системе минус число заявок, находящихся под обслуживанием. Значит (по правилу сложения математических ожиданий) среднее число заявок в очереди L_ОЧ равно среднему числу заявок в системе L_СИСТ минус среднее число заявок под обслуживанием. Число заявок под обслуживанием может быть либо нулем (если канал свободен), либо единицей (если он занят). Математическое ожидание такой случайной величины равно вероятности того, что канал занят P_ЗАН. Очевидно, что:

. (21)

Следовательно, средне число заявок под обслуживанием равно:

, (22)

отсюда

. (23)

По формуле Литтла (9) найдем среднее время пребывания заявки в очереди:

. (24)

n-канальная СМО с неограниченной очередью

Аналогично предыдущей задаче, решается задача об n-канальной СМО с неограниченной очередью. Нумерация состояний – опять по числу заявок, находящихся в системе:

- S₀ – в СМО нет ни одной заявки (все каналы свободны);

- S₁ – занят один канал, остальные свободны;

- S₂ – занято два канала заняты, остальные свободны;

…

- S_k – занято k каналов, остальные свободны;

…

- S_n – заняты все n каналов (очереди нет);

- S_n+1 – заняты все n каналов, одна заявка стоит в очереди;

…

- S_n+r – заняты все n каналов, r заявок стоит в очереди;

…

Условие существования финальных вероятностей: , в противном случае, очередь растет до бесконечности.

Применяя формулы для схемы гибели и размножения, найдем финальные вероятности:

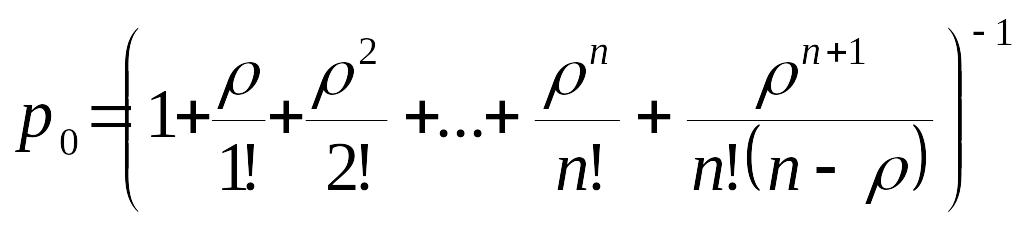, (25)

, , . (26)

Теперь найдем характеристики эффективности СМО. Из них легче всего найти среднее число занятых каналов (это вообще справедливо для любой СМО с неограниченной очередью). Найдем среднее число заявок в очереди L_ОЧ:

. (27)

Прибавляя к нему среднее число заявок под обслуживанием (оно же – среднее число занятых каналов), получим:

. (28)

Деля выражения L_ОЧ и L_СИСТ на , по формуле Литтла получим средние времена пребывания заявок в очереди и в системе:

, . (29)