Расчет характеристик марковских процессов

Рассмотрим, как можно получить дифференциальное уравнение, описывающее марковский процесс. Для этого используем уравнение Колмогорова-Чепмена (1.7.1.) в следующем виде:

.

Проведем следующие преобразования:

,

,

где Е – единичная матрица.

Тогда искомое дифференциальное уравнение в матричной форме примет следующий вид:

, (1.8.1)

где - матрица интенсивностей переходов.

Систему дифференциальных уравнений можно получить непосредственно из графа состояний. Например, имеем граф марковского процесса (рис. 1.8.2).

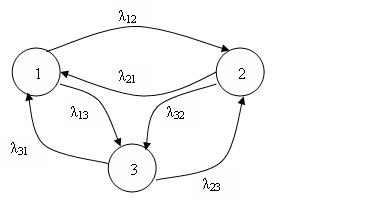
Рис. 1.8.2 Граф марковского процесса с тремя состояниями

Матрица вероятностей переходов для данного случая:

.

В свою очередь матрица интенсивностей переходов имеет вид:

.

На основе матричной записи дифференциального уравнения (1.8.1.) запишем систему уравнений:

Анализ полученной системы дает возможность сформулировать правило составления таких систем: для произвольного момента времени производная от вероятности i‑^го состояния равна сумме произведений всех других вероятностей на интенсивности перехода из них в i-^ое состояние "минус" произведение вероятности i‑^го состояния на суммарную интенсивность выхода из i‑^го состояния.

Полученное правило можно записать в виде формулы:

.

Для установившегося режима и система дифференциальных уравнений преобразуется к системе линейных алгебраических уравнений, решением которой являются финальные вероятности состояний системы. Определение финальных вероятностей рассмотрим на примере.

Пример. Система может находиться в двух состояниях. Для описания модели системы составим граф марковского процесса (рис.1.8.3).

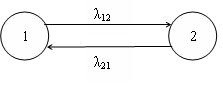
Рис. 1.8.3 Граф марковского процесса с двумя состояниями

Требуется определить финальные значения вероятностей состояний , .

Решение.

Для определения вероятностей составим систему дифференциальных уравнений:

.

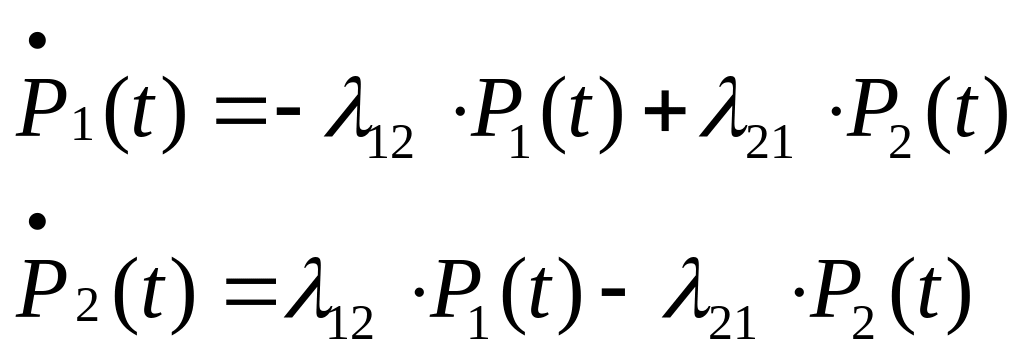Чтобы получить финальные значения вероятностей необходимо перейти к алгебраическим уравнениям:

После замены любого уравнения на нормирующую сумму решение системы становится очевидным:

, .

Модель "гибели и размножения"

Схема "гибели и размножения" часто встречается в разнообразных практических задачах. Своим названием эти процессы обязаны биологической задаче об изменении численности популяции и распространением эпидемий.

В технических системах данной моделью описывают процессы возникновения отказа и восстановления.

Процесс "гибели и размножения" может быть представлен марковским случайным процессом с непрерывным временем, причем число состояний может быть бесконечным или конечным. В этом случае интервалы времени между двумя моментами рождения и гибели распределены по экспоненциальному закону.

Таким образом, марковский процесс называется процессом "гибели и размножения", если его граф состояний (рис. 1.8.4) имеет вид цепочки состояний, в которой каждое состояние (кроме крайних) связано с двумя соседними состояниями, а крайние состояния только с соседним состоянием.

Рис. 1.8.4 Схема "гибели и размножения"

Для такого графа достаточно просто определяются финальные вероятности состояний. Действительно

- для нулевого состояния,

- для первого состояния, и т.д.

- для последнего состояния.

В итоге получилась система уравнений.

Добавим к ней нормировочное уравнение .

Вероятность всех состояний выразим через вероятность нулевого состояния:

,

,

…

После подстановки вероятностей в нормировочное уравнение выражение для определения вероятности нулевого состояния примет следующий вид:

.

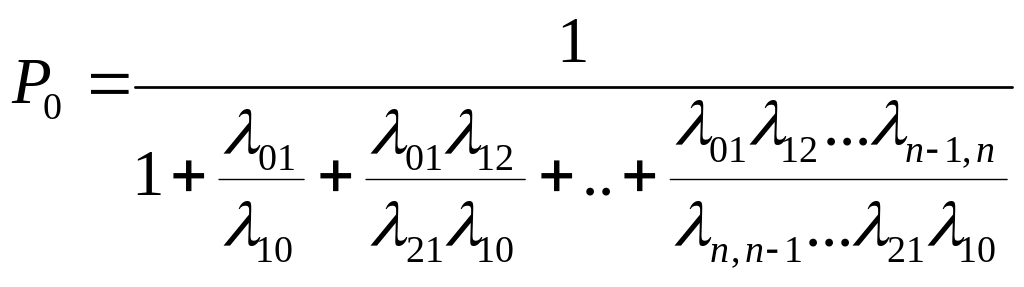Значения остальных вероятностей рассчитываются по полученным ранее соотношениям.