Анализ марковских цепей

Результатом анализа марковской цепи являются ответы на два вопроса:

• как при известном начальном состоянии от шага к шагу меняются вероятности состояний, в которых может находиться система,

• каковы установившиеся значения этих вероятностей.

Покажем, как решается данная задача.

Имеем вектор-строку .

В начальный момент времени состояние известно: .

Для расчета вероятностей используем уравнение Колмогорова-Чепмена:

, (1.7.1)

где Р - матрица вероятностей переходов.

С помощью уравнения Колмогорова-Чепмена можно вычислить вероятности состояний рекуррентно, т.е. последовательно:

,

,

,

…

.

При n→∞ можно определить установившиеся (финальные) вероятности. Для этого необходимо решить уравнение:

,

где .

Пример 1. Вероятностный автомат представлен в виде графа, изображенного на рисунке 1.7.2.

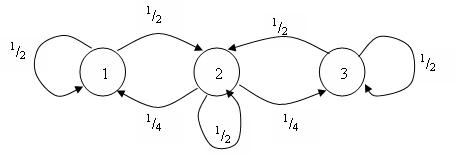
Рис. 1.7.2 Граф вероятностного автомата

Требуется определить, как меняется вектор вероятностей состояний , если и чему равны финальные вероятности.

Решение. На основе графа (рис. 1.7.2) составим матрицу вероятностей:

.

Для определения векторов вероятностей состояний используем уравнение Колмогорова-Чепмена (1.7.1):

,

,

и т.д.

Для определения финальных вероятностей составим уравнение:

.

Это уравнение равносильно системе уравнений:

Для однозначного решения системы добавим нормирующую сумму . Тогда из второго уравнения следует, что .

Значения остальных вероятностей очевидны:

и .

Марковские процессы Понятие о марковских процессах с непрерывным временем переходов

Марковские процессы с непрерывным временем переходов можно рассматривать как марковские цепи, если разбить время на малые интервалы ∆t и определить вероятности p_ij за ∆t. При равных интервалах эти вероятности, для того, чтобы процесс был марковским, должны быть постоянными. В противном случае поведение будет зависеть от предыстории, в данном случае от того, как долго система находится в i^-ом состоянии.

Вероятность p_ij при малых ∆t равна , где - постоянный коэффициент, называемый интенсивностью перехода из i^-го состояния в j^-е состояние.

Возникает вопрос, какому закону распределения должно подчиняться время перехода?

В соответствии с марковским свойством вся предыстория процесса сказывается на его поведении в будущем только через текущее состояние, которое и определяет дальнейший ход процесса.

Таким образом, нет необходимости знать, как долго процесс находится в текущем состоянии. Отсюда следует, что распределение остающегося времени пребывания процесса в состоянии s_j должно зависеть только от самого состояния, а не от времени пребывания в нем. Этим свойством обладает только одно распределение – экспоненциальное.

Таким образом, непременное свойство непрерывного марковского процесса – экспоненциальность распределения времени пребывания процесса в каждом из состояний.

Марковский процесс с непрерывным временем переходов можно задать в виде графа (рис. 1.8.1) или описать системой дифференциальных уравнений.

Для определения финальных вероятностей состояний дифференциальные уравнения преобразуются в систему линейных уравнений.

Рис. 1.8.1 Граф марковского процесса

Иногда марковский процесс с дискретными состояниями, переходы между которыми разрешаются в любой момент времени, называется непрерывной марковской цепью.