
- •Курс лекций по дисциплине «Моделирование инфокоммуникационных систем» Общие сведения и порядок изучения дисциплины
- •Структура и содержание дисциплины
- •Содержание (дидактика) дисциплины
- •Раздел 1. Математические модели.
- •Лекция 1. Введение в математическое моделирование
- •Понятие инфокоммуникационной системы Информационная система
- •Классификация информационных систем
- •Разработка и реализация проектов инфокоммуникационных систем
- •Моделирование как процесс
- •Природа и математическое мышление
- •Лекция 2. Форма и принципы представления математических моделей Введение Общие понятия и принципы теории моделирования
- •Принцип одномерности конечного решения
- •Классификация моделей
- •Формализация процесса функционирования системы
- •Разработка концептуальной модели
- •Разработка математической модели (мм)
- •Лекция 3. Типовые математические модели
- •Примеры моделей Оптимизационные модели
- •Основные подходы к моделированию
- •И спользование законов природы
- •Принцип аналогии
- •Использование типовых моделей
- •Иерархический подход к получению моделей
- •Конечные автоматы Понятие конечного автомата
- •Задание автомата в виде таблицы и графа
- •Матричное задание автомата
- •Минимизация конечных автоматов
- •Аналитическое задание конечных автоматов
- •Вероятностные автоматы Общие сведения о вероятностных автоматах
- •Марковские цепи с дискретным временем
- •Анализ марковских цепей
- •Марковские процессы Понятие о марковских процессах с непрерывным временем переходов
- •Расчет характеристик марковских процессов
- •Модель "гибели и размножения"
- •Модели массового обслуживания Области применения. Основные понятия
- •Простейший поток заявок
- •Рекуррентные потоки. Формула Литтла
- •Системы массового обслуживания и их характеристики
- •Одноканальная смо с неограниченной очередью
- •Более сложные задачи теории массового обслуживания
Задание автомата в виде таблицы и графа
Автомат может быть задан своими функциями (переходов и выхода), таблично, в виде графа, матрицы, а также аналитически.
Для табличного представления нужно перечислить все сочетания x(t), u(t) – все элементы области определения функций переходов и выхода (область определения одна и та же) и записать соответствующие им значения x(t+1) и y(t) – элементы областей значения функций переходов и выхода.
Для наглядности аргументы x и u имеет смысл разделить: значения одного аргумента приписать строкам, а другого – столбцам. Тогда значение функций будут записываться на пересечении строк и столбцов. Ввиду совпадения областей определения функций переходов и выхода эти функции можно задавать одной таблицей.
При изображении функций в виде графа: состояния приписывают вершинам, управления – дугам.
Пример 1. Пусть множество управлений u состоит из управлений α, β, γ, множество состояний x – состояний 1,2,3,4, т.е. uα, β, , x1,2,3,4, y 0,1.
Функции φ (переходов) и (выхода) заданы таблицей переходов (табл. 1.4.1), в которой единица может означать необходимость какого-либо действия, ноль – отсутствие такового, прочерк – ограниченность управлений (отсутствует управление β при состоянии 2 и управление γ при состоянии 3).
Таблица 1.4.1
x(t) |
u(t) |
||
α |
β |
|
|
1 |
2/0 |
3/1 |
4/0 |
2 |
2/1 |
- |
3/0 |
3 |
3/0 |
4/0 |
- |
4 |
2/1 |
1/0 |
2/1 |
При другом способе задания конечного автомата используется понятие направленного графа.
Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершины дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал вызывает переход из одного состояния в другой, то на графе автомата дуга, соединяющие их вершины обозначается соответствующим символом входного сигнала. Для задания функции выходов дуги графа необходимо отметить соответствующими сигналами.
Табл. 1.4.1.соответствует граф, показанный на рис. 1.4.1.
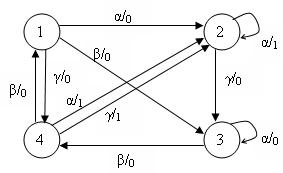
Рис.1.4.1 Граф конечного автомата таблицы 1.4.1.
Пример 2. Рассмотрим автомат, который выдает билет при опускании в него монет в сумме 3 руб., причем он принимает монеты 50 коп., 1рубль и 2 рубля. Автомат может давать сдачу. Составим функцию перехода и выхода.
u α=0.5, β=1, =2, x1,2,3,4,5,6.
Функция переходов может быть задана таблицей переходов (табл. 1.4.2).
Таблица 1.4.2
-
u
0.5
1.0
2.0
x
β
0
1

2
3
5
0.5
2
3
4
6
1.0
3
4
5
1
1.5
4
5
6
1
2.0
5
6
1
1
2.5
6
1
1
1
Поясним табл. 1.4.2.
Например, опустили в автомат 1 рубль. Тогда из исходного состояния 1 (ожидание начала набора суммы) автомат перешел в состояние 3 (в автомате пока накопилась сумма 1 рубль). Теперь опустили, к примеру, 50 коп., тогда автомат перейдет из теперь уже исходного состояния 3 в состояние 4 (в автомате уже полтора рубля), далее опустили еще 1 рубль – автомат перешел из состояния 4 в состояние 6 (накопилась сумма 2,5 рубля). И, наконец, опустили последние 50 коп., в автомате собралась полная сумма: выдается билет, и автомат опять переходит в 1 состояние – готовности к приему монет.
Для функции выхода y = (y1, y2) составим табл. 1.4.3, в которой:
y1 – сигнал на пропуск или выдачу билета, y1 0,1.
y2 – сигнал для сдачи, y2 0, 0.5, 1.0, 1.5.
Таблица 1.4.3
-
u
0,5
1
2
x
β
1
0;0
0;0
0;0
2
0;0
0;0
0;0
3
0;0
0;0
1;0
4
0;0
0;0
1;0,5
5
0;0
1;0
1;1
6

1;0
1;0,5
1;1,5
действие сдача
При превышении требуемой цены за билет вместе с билетом выдается сдача. Моменты времени лучше связывать только с моментами опускания монеты.
