МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

Государственное образовательное учреждение высшего профессионального образования

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРИКЛАДНОЙ БИОТЕХНОЛОГИИ (МГУПБ)

Кафедра технологического оборудования и процессов отрасли

ОСНОВЫ МЕХАТРОНИКИ

А.Я. Красинский, А.А. Халиков, Д.Р. Каюмова

РАСЧЕТ ПОКАЗАТЕЛЯ РАСПРЕДЕЛЕНИЯ ФУНКЦИОНАЛЬНОЙ НАГРУЗКИ МЕХАТРОННЫХ СИСТЕМ

Методические указания к самостоятельной работе

для студентов специальностей

220401 – Мехатроника

260601 – Машины и аппараты пищевых производств

260602 – Пищевая инженерия малых предприятий

и направления подготовки уровня бакалавриата 150400 – Технологические машины и оборудование

Москва 2010

Составители: А.Я. Красинский, д.ф.-м.н., проф.

А.А. Халиков, асп.

Д.Р. Каюмова, асп.

Методические указания составлены в соответствии с рабочей программой по курсу «Основы мехатроники». Цель методических указаний – ознакомление студентов с алгоритмом расчета коэффициента распределения функциональной нагрузки и обучение анализу мехатронных систем с точки зрения распределения функциональной нагрузки.

Предназначены для студентов специальностей 220401 – Мехатроника, 260601 – Машины и аппараты пищевых производств, 260602 – Пищевая инженерия малых предприятий и направления подготовки уровня бакалавриата 150400 – Технологические машины и оборудование.

Утверждены УМС МГУПБ

© МГУПБ, 2011

Введение

Для количественного анализа и оценки мехатронных модулей и сис­тем введена специальная мера - показатель распределения функциональ­ной нагрузки (РФН). Показатель РФН позволяет оценить объем функ­циональной нагрузки, которую несет каждый из структурных элементов или блоков в исследуемой системе. Чем выше значение данного показа­теля, тем большее влияние оказывает данный элемент на качество систе­мы в целом, т.е. ее стоимость, надежность и другие комплексные харак­теристики.

Показатель РФН является численной мерой, которая опреде­ляет важность структурной единицы (элемента, группы элементов, под­системы) на основе наличия и числа ее связей с другими элементами сис­темы. Чем выше ранг данного узла, тем большую функциональную на­грузку он несет, тем больше он влияет на качество системы в целом.

1. Алгоритм расчета показателя рфн

Метод определения показателя РФН, изучаемый в данном пособии, заключается в анализе значимости структурных элементов и основан на теории графов и матриц. Краткие сведения о теории графов можно получить в [2].

1. Структурная схема исследуемой системы представляется в виде ориентированного графа , где множество вершин состав­ляют структурные элементы системы, а множество ребер отображает связи между ними. Для геометрического представления ориентированное ребро показывается в виде дуги со стрелкой, направление которой совпадает с направлением потока энергии или информации между соединяемыми вершинами. Рассматриваются только связные графы, в которых для любой пары вершин существует соединяющий их путь.

2. Для построенного графа формируется матрица смежности . Пусть структура системы содержит вершин , соединенных ребрами . Тогда получаем матрицу размером , которая состоит из нулей и единиц. Элемент матрицы , если граф содержит ребро , направленное от вершины к -му узлу. В противном случае принимается, что . Число единичных элементов в матрице будет равно числу ребер.

3. Определяем матрицу по следующей формуле:

,

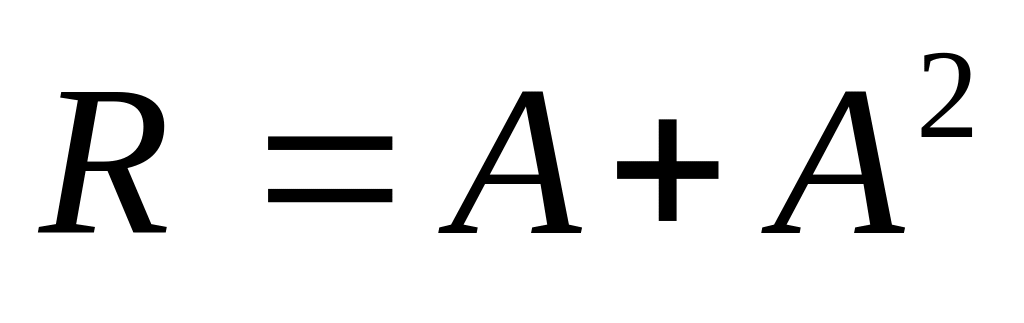(1)

где - матрица смежности.

4. Ранг элемента определяется как сумма элементов -й строки матрицы :

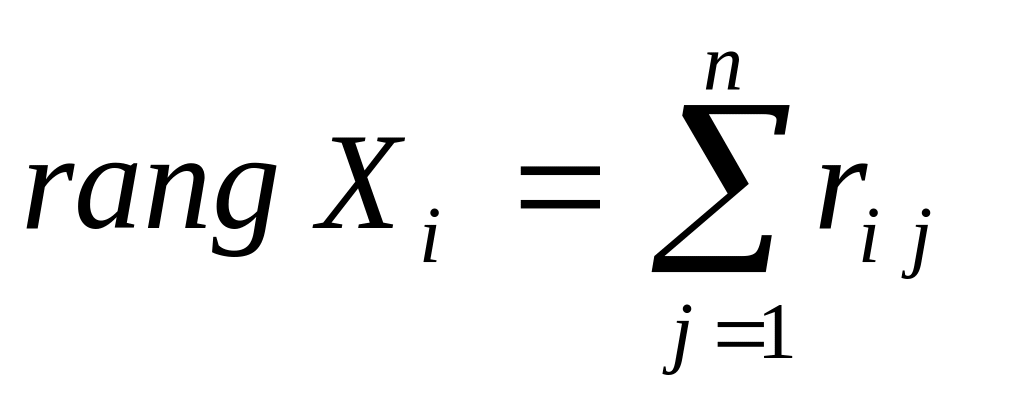
(2)

5. Показатель РФН для структурного элемента определяется выражением:

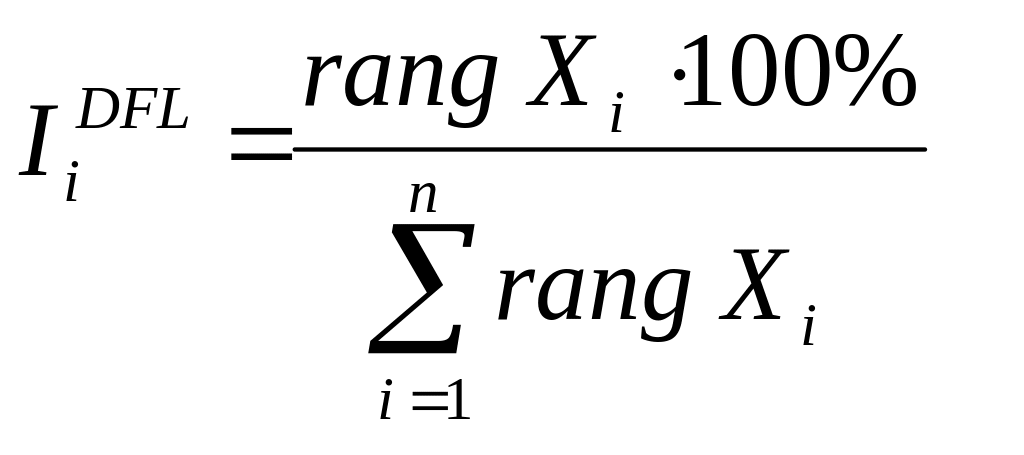. (3)

Из формулы следует, что значение этого показателя определя­ется в процентном соотношении и нормализуется таким образом, что сумма показателей РФН всех элементов системы единична для любого исходного графа, т.е.

Такая нормализованная форма удобна для сравнительного анализа распределения функциональной нагрузки в системах различной сложно­сти и с различными типами структуры.

6. Расчет общего показателя РФН группы элементов, входящих в определенную подсистему , производится суммированием показателей РФН составляющих элементов. Например, если заданная группа состоит из элементов, тогда показатель РФН группы получается как сумма показателей:

.

(4)

Для оценки функциональной нагрузки целесообразно определить значение показателя РФН для элементов данной группы:

.

(5)

7. Ранжирование элементов мехатронной системы производится на основе значений их показателей РФН и делается заключение о распреде­лении функциональной нагрузки в исследуемой системе.

2. Пример

Представленную методику расчета показателя РФН рассмотрим на примере одного варианта системы управления робота "PUMA-560". Структура исследуемой систе­мы (рис. 1) включает в себя как управляющую подсистему (контроллер движения), так и электромехани­ческую часть (электродвигатель и фотоимпульсные датчики обратной связи), которая будет неизменной при выполнении всего анализа.

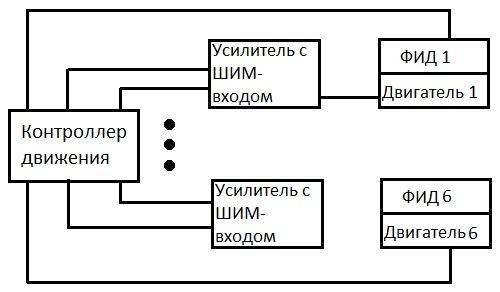
Рис.1. Структура системы управления робота «PUMA-560» на основе контроллера движения

1. Построим граф , представляющий структурную модель рассматриваемой системы (рис. 2).

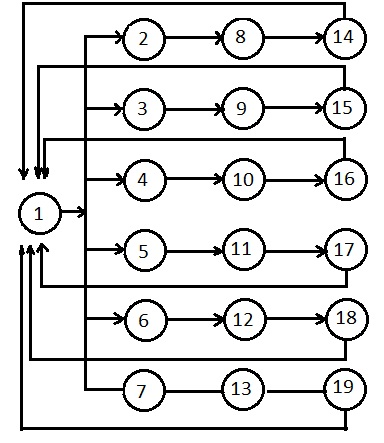
Рис. 2. Граф, представляющий структурную модель системы

2. Для графа составим матрицу смежности :

Дальнейший расчет будет проводиться на компьютере с использованием языка Python¹ [3, 4] и библиотеки NumPy². Python – это мощный и простой в использовании мультипарадигменный язык программирования позволяющий решать самые разные задачи от простых сценариев (скриптов) до сложных научно-технических задач. В состав Python входит большое число функциональных возможностей, известных как стандартная библиотека. Кроме того, Python допускает расширение как за счет ваших собственных библиотек, так и за счет библиотек, созданных сторонними разработчиками. Одним из таких расширений является NumPy – библиотека численных вычислений, позиционируемая как свободный и более мощный эквивалент системы математических вычислений Mathlab.

Для работы необходимо запустить программу IDLE³. Когда Python установлен в Windows, его можно найти в меню Пуск (Start). Набор пунктов меню может немного отличаться в зависимости от версии, но пункт IDLE запускает среду разработки с графическим интерфейсом, а пункт Python запускает сеанс работы с интерактивной командной оболочкой (консолью). Кроме того, здесь можно увидеть пункты вызова стандартного справочного руководства - Python Manuals.

Чтобы использовать функции NumPy нужно импортировать соответствующую библиотеку, выполнив команду:

>>> import numpy

Введем матрицу в компьютер:

>>> A = numpy.matrix([[0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1], [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]])

3. Определим матрицу по формуле (1):

>>> R = A + A**2

4. Определим ранг структурных элементов по формуле (2):

>>> X = numpy.zeros([19, 1]) # создаем вектор X >>> for i in range(0, 19): for j in range(0, 19): X[i] += A[i, j] >>> print X # вывод на экран вектора X

5. Определим показатель РФН:

>>> S = numpy.sum(X) # cумма элементов вектора X >>> I = zeros([19, 1]) # создаем вектор I >>> for i in range(0, 19): I[i] = (X[i] * 100)/S >>> print I # вывод на экран вектора I