
- •Оглавление
- •1Введение
- •2Основные методы математической статистики
- •2.1Способы первичной обработки выборки
- •2.2Точечные оценки параметров распределения
- •2.3Интервальные оценки параметров распределения
- •2.4Определение параметров функциональной зависимости методом наименьших квадратов
- •3 Элементы теории корреляции
- •3.1Линейная корреляция
- •3.2Ранговая корреляция
- •Задача 1
- •Задача 2
2.2Точечные оценки параметров распределения
По имеющейся выборке можно дать оценку математического ожидания и дисперсии генеральной совокупности. Оценкой математического ожидания служит выборочное среднее
![]() (2)
(2)
то есть среднее арифметическое всех элементов выборки, а оценкой дисперсии – выборочная дисперсия
![]() (3)
(3)
Заданная таким
образом оценка математического ожидания
является несмещенной,
то есть математическое ожидание
выборочного среднего равно оцениваемому
параметру (математическому ожиданию
исследуемой случай-ной величины).
Выборочная дисперсия, напротив, смещенная
оценка генеральной дисперсии, и
![]() Поэтому вводится несмещен-ная оценка
генеральной дисперсии – исправленная
выборочная дисперсия
Поэтому вводится несмещен-ная оценка
генеральной дисперсии – исправленная
выборочная дисперсия
![]() (4)
(4)
Соответственно
число
![]() является несмещенной точечной оценкой
среднего квадратического отклонения.
является несмещенной точечной оценкой
среднего квадратического отклонения.
2.3Интервальные оценки параметров распределения
Точечная оценка
при малом объеме выборки может существенно
отличать-ся от оцениваемого параметра,
поэтому важно знать, насколько истинное
значение параметра может отклоняться
от найденной точечной оценки. Интервал
вида
![]() где Ө -
истинное значение оцениваемого параметра,
а Ө*
- его точечная оценка, называется
доверительным
интерва-лом,
а вероятность
где Ө -
истинное значение оцениваемого параметра,
а Ө*
- его точечная оценка, называется
доверительным
интерва-лом,
а вероятность
![]() доверительной
вероятностью или
надежностью.
Для построения доверительного интервала
требуется знать закон распределения
исследуемой случайной величины. Пусть
эта величина распределена по нормальному
закону. Если при этом известно ее среднее
квадратическое отклонение σ,
то доверительный интервал для
математичес-кого ожидания имеет вид:
доверительной
вероятностью или
надежностью.
Для построения доверительного интервала
требуется знать закон распределения
исследуемой случайной величины. Пусть
эта величина распределена по нормальному
закону. Если при этом известно ее среднее
квадратическое отклонение σ,
то доверительный интервал для
математичес-кого ожидания имеет вид:
![]() (6)
(6)
где а
– оцениваемое математическое ожидание,
хВ
– выборочное среднее, п
– объем выборки, t
– такое значение аргумента функции
Лапласа Ф
(t),
при котором
![]()
При неизвестном среднем квадратическом отклонении доверительный интервал для математического ожидания при заданной надежности γ задается так:
![]() (7)
(7)
Здесь s
– исправленное выборочное среднее
квадратическое отклонение, а
![]() критическая точка распределения
Стьюдента, значение которой можно найти
из таблиц по известным п
и γ.
критическая точка распределения
Стьюдента, значение которой можно найти
из таблиц по известным п
и γ.
Для оценки генерального среднего квадратического отклонения σ при заданной надежности γ можно построить доверительный интервал вида
![]() (7)
(7)
где s – исправленное выборочное среднее квадратическое отклонение, а q = q (n, γ) – значение, определяемое из таблиц.
2.4Определение параметров функциональной зависимости методом наименьших квадратов
При совместном
исследовании двух случайных величин
по имеющейся выборке (х1,
у2),
(х2,
у2),…,(xk,
yk)
возникает задача определения зависимости
между ними. Если вид функции y
= f
(x,
a,
b,...)
задан, то требуется найти значения
коэффициентов a,
b,...,
при которых yi
наименее отличаются от f
(xi).
В методе наименьших квадратов коэффициенты
должны быть такими, что
![]() принимает минимальное значение.
принимает минимальное значение.
а) Линейная
зависимость y
= ax
+ b.
Если
![]() ,
то из условия
,
то из условия
![]() получаем:
получаем:
 (8)
(8)
б) Квадратичная
зависимость y
= (ax
+ b)2.
Отсюда
![]() и система для определения a,
b
может быть получена по аналогии с
предыдущим случаем с помощью замены yi
на
и система для определения a,
b
может быть получена по аналогии с
предыдущим случаем с помощью замены yi
на
![]() :
:
 (9)
(9)
в) Показательная
зависимость![]() Логарифмируя,
получаем: lny=ax
+ b,
и система уравнений для a,
b
имеет вид:
Логарифмируя,
получаем: lny=ax
+ b,
и система уравнений для a,
b
имеет вид:
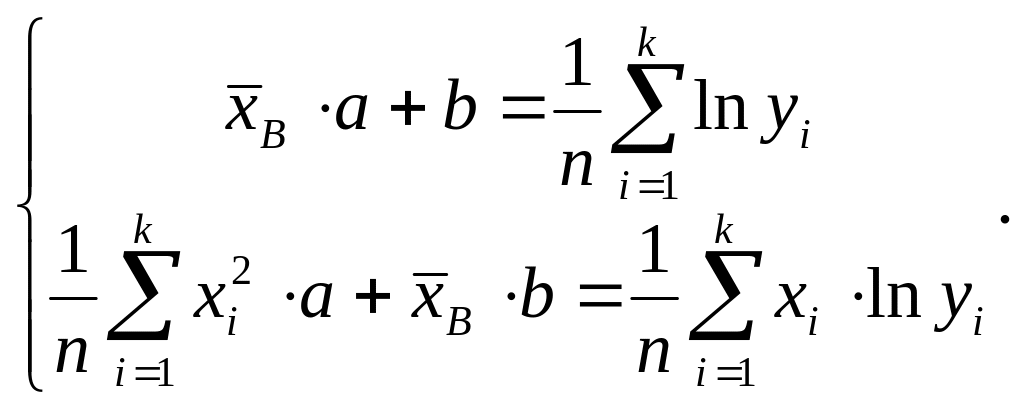 (10)
(10)
г) Зависимость
вида
![]() Тогда y2
= ax
+ b,
и условия для а
и b
можно задать так:
Тогда y2
= ax
+ b,
и условия для а
и b
можно задать так:
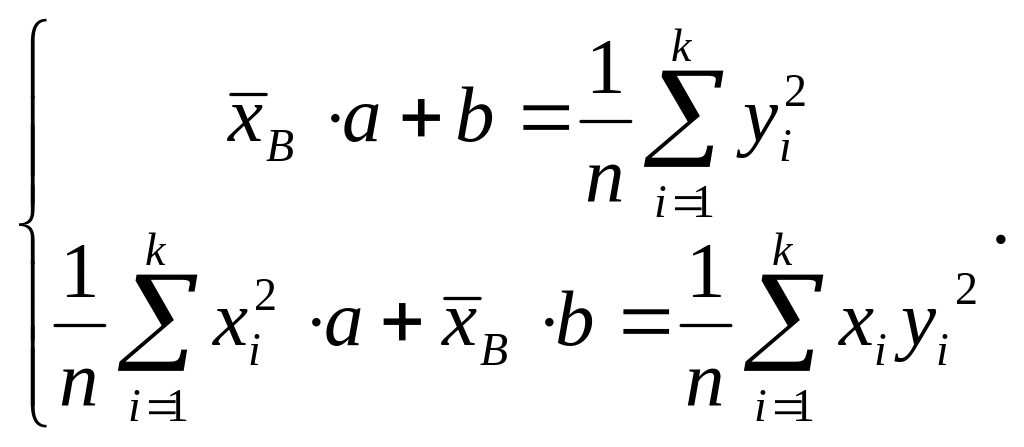 (11)
(11)
д) Логарифмическая зависимость y = ln(ax + b), то есть ey = ax + b, и
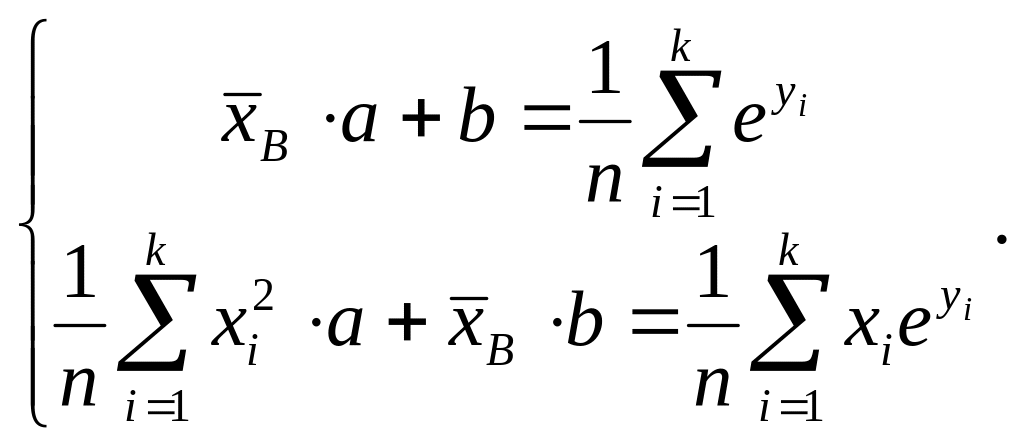 (12)
(12)
