5.1.3. Interpft - Апроксимація періодичної функції,
базуючись на швидкому перетворенні Фур’є
Синтаксис:
yp = interpft(y, n)
Опис:
Функція yp = interpft(y, n) повертає одномірний масив чисел, який є періодичною функцією, визначеною у n точках і апроксимуючою одномірний масив y. Якщо length(x) = m, а інтервал дискретності dx, то інтервал дискретності для y визначається за формулою dy = dx * m/n, при цьому n завжди перевищує m.
Приклад:
Розглянемо апроксимацію функції y = sin(x), яка задана 11 точками на інтервалі [0 10].
x = 0:10; y = sin(x); xp = 0:0.25:10; yp = interpft(y, 41); xt = 0:0.01:10; yt = sin(xt); plot(xt, yt, 'r'), hold on, plot(x, y, 'ob', xp, yp)
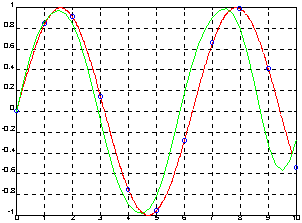
На графіку побудована точна функція y = sin(x) з вказівкою точок збирання даних та її апроксимація у 41 точці. Як видно з графіка, апроксимація зовні інтервалу [0 1.5] має зростаючу похибку.
5.1.4. Spline - Інтерполяція функції однієї змінної кубічним сплайном
Синтаксис:
yi = spline(x, y, xi) |
v = pp val(pp, xx) |
pp = spline(x, y) |
[breaks, coefs, l, k] = unmkpp(pp) |
|
pp = mkpp(breaks, coefs) |
Опис:
Функція yi = spline(x, y, xi) інтерполює значення функції y точках xi усередині області визначення функції, використовуючи кубічні сплайни [1].
Функція pp = spline(x, y) повертає pp-форму сплайна, що використовується у М-файлах ppval, mkpp, unmkpp.
Функція v = ppval(pp, xx) розраховує значення частково гладкого полінома pp для значень аргументу xx.
Функція [breaks, coefs, l, k] = unmkpp(pp) повертає характеристики частково гладкого полінома pp: breaks - вектор розбиття аргументу; coefs - коефіцієнти кубічних сплайнів;
l = length(breaks) - 1; k = length(coefs)/l.
Функція pp = mkpp(breaks, coefs) формує частково гладкий поліном pp за його характеристиками.
Приклад:
Задамо синусоїду усього лише 10 точками та виконаємо інтерполяцію кубічними сплайнами, використовуючи дрібну сітку.
x = 0:10; y = sin(x); xi = 0:.25:10; yi = spline(x, y, xi); plot(x, y, 'o', xi, yi, ‘g’), grid
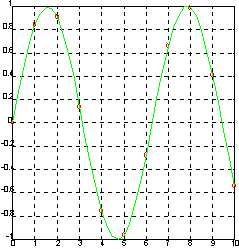
Визначимо pp-форму сплайна.
pp = spline(x, y); [breaks, coeffs, l, k] = unmkpp(pp) breaks = 0 1 2 3 4 5 6 7 8 9 10 coeffs =
-0.0419 |
-0.2612 |
1.1446 |
0 |
-0.0419 |
-0.3868 |
0.4965 |
0.8415 |
0.1469 |
-0.5124 |
-0.4027 |
0.9093 |
0.1603 |
-0.0716 |
-0.9867 |
0.1411 |
0.0372 |
0.4095 |
-0.6488 |
-0.7568 |
-0.1234 |
0.5211 |
0.2818 |
-0.9589 |
-0.1684 |
0.1509 |
0.9538 |
-0.2794 |
-0.0640 |
-0.3542 |
0.7506 |
0.6570 |
0.1190 |
-0.5463 |
-0.1499 |
0.9894 |
0.1190 |
-0.1894 |
-0.8856 |
0.4121 |
l = 10 k = 4 Розрахуємо pp-форму у вузлових точках сітки.
0 |
0.8415 |
0.9093 |
0.1411 |
-0.7568 |
-0.9589 |
-0.2794 |
0.6570 |
0.9894 |
0.4121 |
-0.5440 |
v = ppval(pp,x) v =
Алгоритм:
Інтерполяція сплайнами використовує допоміжні функції ppval, mkpp, unmkpp, які створюють невеликий пакет для роботи з частково гладкими поліномами.
Суттєво великі можливості для роботи зі сплайнами пропонує користувачеві спеціальний пакет Spline Toolbox [2].