§ 1.3. Операции над множествами.

Опр. 5 Объединением множеств A и B называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств A и B.

Обозначение операции объединения А  В ( - Unit)

Символически записать определение операции объединения можно т.о.

A  B = { x | x A или x B }

Если элемент является элементом и A, и B, то в AB он не удваивается.

Аналогично определяется объединение произвольной (в том числе бесконечной) совокупности множеств. Если совокупность содержит небольшое количество множеств, то их объединение описывается явно:

A

 B  C  D

В общем случае используется обозначение

которое читается так: «объединение всех множеств A, принадлежащих совокупности S».

Если все множества занумерованы индексами, то используются другие варианты обозначений:

, когда S = {A₁, A₂,..., A_k}

, если S – бесконечная совокупность, и ее множества занумерованы натуральными числами.

,если набор индексов задан множеством I.

Пример 2.

а. A = {a, b, d}; B = {b, d, e, h}

A B = {a, b, d, e, h}

б. M₃ и M₄ из примера 1.

M₃  M₄ = M₃ = M₄ (т.к. M₃ и M₄ равны)

в. Обозначим учебные группы студентов курса через Гр_i.

M₇ = {Гр1, Гр2, …, Гр12}

- множество всех студентов курса (но не групп)

Заметим, что но неверно, что

г. Обозначим через N_k множество всех натуральных чисел, делящихся на k и не равных k, а через P – множество всех простых чисел (принято считать, что 1 P).

Тогда - множество всех составных, т.е. непростых чисел.

Опр. 6 Пересечением множеств A и B называется множество, состоящее из тех и только тех элементов, которые принадлежат и множеству A, и множеству B.

Обозначается: А  В

Запишем определение символически

A  B = { x | x A и x B }

Аналогично определяется пересечение произвольной (в том числе бесконечной) совокупности множеств. Обозначения для пересечения системы множеств аналогичны обозначениям для объединения.

Пример 3.

а. A= {a, b, d}; B= {b, d, e, h}

A B= {b, d}

б. M₃ M₄=M₃=M₄

 Грj =

Опр. 7 Разностью множеств A и B называется множество всех тех и только тех элементов A, которые не содержатся в B. Обозначается А \ В

Символическая запись определения:

A \ B = { x | x A и x  B }

В отличие от двух предыдущих операций разность, во-первых, строго двухместна (т.е. определена только для двух множеств), а во-вторых, некоммутативна, т.е. A \ B B \ A.

Если A \ B = , то A B

Пример 4

a) A= {a, b, d}, B= {b, d, e, h}

A \ B = {a}

B \ A = {e, h}

б) M₃ \ M₄ = M₄ \ M₃ = 

Если все рассматриваемые множества представляют собой конечную совокупность, то их объединение представляет собой универсальное множество E. В этом случае может быть определена операция дополнения.

Опр. 8 Дополнением (до E) множества A называется множество всех элементов, не принадлежащих A. Обозначается .

Операторная запись: = E \ A, где E-универсальное множество.

Символическая запись: = { x | x A }

Пример 5.

а. E-все студенты группы 2206.

A-множество спортсменов из числа E.

-множество студентов - не спортсменов гр. 2206.

б. Из примера 1 ₂ - множество натуральных чисел >12

Операции объединения, перечисления и дополнения называют булевыми операциями над множествами. Все операции над множествами можно интерпретировать в виде диаграмм Венна.

Объединение 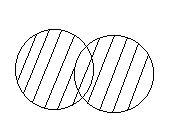Пересечение

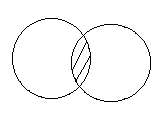
Вычитание A\B 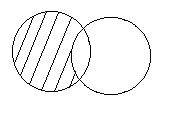Дополнение

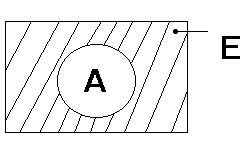
Задачи

1. Задайте перечислением а) множество М₂; б) множество М₇.

2. Найти мощность множества D₁ простых делителей числа 30.

3. Найти мощность множества D₂ простых делителей числа 64.

4. Найти строгие подмножества множества D₁ из примера 1.

5. Найти строгие подмножества множества D₂ из примера 2.

6. Привести примеры множества множеств.

Теория типов. Объекты имеют тип 0, множества - тип 1, множества множеств – тип 2 и т.д.

7. Пусть по определению А={{1,2,3},{1,3,},1,2}.

Верно ли, что {1,2}  А? {1,2}  А?

8. Пусть M₆ – множество студентов группы 2206

M₇ – множество групп факультета 2.

M₈ – множество студентов факультета 2.

Как относятся множества: M₆ и M₇? M₆ и M₈? (Ответ: M₆ M_7, M₆  M₈)

Верно ли, что M₇ = M₈?

9. Как соотносятся объекты а и а?

Привести примеры одноэлементных множеств.

10. Привести (придумать) примеры таких множеств А,B,C,D, чтобы выполнялись условия:

11. а) A  B, B  C, C  D;

б) A  B, B  C;

в) A  B, B  C, C  D;

г) A  B, A  B.

12. Пусть Д – множество девушек группы 2206, Ю – множество юношей группы 2206, О – множество отличников группы 2206.

13. Найти

а) Д  Ю;

б) Д  О;

в) Ю  О;

г) М₆ \ Ю;

д) М₆ \ Д.

14. Найти объединение элементов множества М₇. Найти все парные пересечения элементов множества М₇. Найти пересечение всех элементов множества М₇.