Применение

Поток Пуассона служит для моделирования различных реальных потоков: несчастных случаев, потока заряженных частиц из космоса, отказов оборудования и других. Так же возможно применение для анализа финансовых механизмов, таких как поток платежей и других реальных потоков. Для построения моделей различных систем обслуживания и анализа их пригодности.

Использование потоков Пуассона значительно упрощает решение задач систем массового обслуживания, связанных с расчетом их эффективности. Но необоснованная замена реального потока потоком Пуассона там, где это недопустимо, приводит к грубым просчетам.

4.Марковский процесс

Ма́рковский проце́сс — случайный процесс, эволюция которого после любого заданного значения временно́го параметра t не зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано («будущее» процесса не зависит от «прошлого» при известном «настоящем»; другая трактовка (Вентцель): «будущее» процесса зависит от «прошлого» лишь через «настоящее»).

Процесс Маркова — модель авторегрессии AR(1): x_t=ψ₁*x_t-1+ε_t

История

Определяющее марковский процесс свойство принято называть марковским; впервые оно было сформулировано А. А. Марковым, который в работах 1907 г. положил начало изучению последовательностей зависимых испытаний и связанных с ними сумм случайных величин. Это направление исследований известно под названием теории цепей Маркова.

Однако уже в работе Л. Башелье можно усмотреть попытку трактовать броуновское движение как марковский процесс, попытку, получившую обоснование после исследований Винера в 1923.

Основы общей теории марковских процессов с непрерывным временем были заложены Колмогоровым.

Отличие Марковского процесса от Марковской цепи

Марковская цепь с дискретным временем — время дискретно, пространство состояний дискретно.

Марковская цепь с непрерывным временем — время непрерывно, пространство состояний дискретно

Марковский процесс — и время и пространство состояний непрерывно.

5.Стационарные процессы

Стационарный случайный процесс

На практике часто встречаются случайные процессы, протекающие однородно во времени. Они имеют вид непрерывных случайных колебаний вокруг неслучайного значения. Амплитуда и характер колебаний в среднем не меняются со временем, такие процессы называются стационарными. Например: колебание напряжения, давление газа в газопроводе, колебание самолета вокруг центра тяжести. У стационарного с.п. X(t) все вероятностные характеристики не должны зависеть от времени. Рассмотрим одномерную плотность распределения стационарного случайного процесса f(t,x). Так как эта плотность не зависит от того, где взято сечение t, то имеет место равенство f(t1,x) = f(t2,x) = … = f(x)

Зная одномерную плотность стационарного с.п. X(t), можно найти его м.о. и дисперсию: , . Таким образом, у стационарного с.п. математическое ожидание и дисперсия являются постоянными величинами, не зависящими от времени.

Рассмотрим n сечений стационарного с.п. X(t), взятых в моменты времени t1, t2, …, tn; n-мерную плотность распределения можно записать в виде: fn( t1, t2, … , tn; x1, x2,…,xn ). Очевидно, что если с.п. является стационарным, то эта n-мерная плотность распределения не изменится при сдвигу всех аргументов на одинаковую величину τ fn( t1, t2, … , tn; x1, x2,…,xn ) = fn( t1 + τ, t2 + τ, … , tn + τ; x1, x2,…,xn ).

Случайный процесс X(t) называется стационарным в узком смысле, если его n-мерная плотность распределения не изменяется при сдвиге всех его аргументов на одинаковую произвольную величину τ.

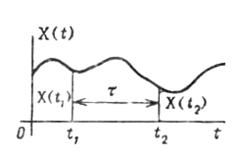Обозначим τ = t2 – t1, тогда f2(t1, t2, x1, x2) = f2(τ, x1, x2). Случайный процесс называется стационарным в широком смысле, если его математическое ожидание постоянно (mx = const), а корреляционная функция есть функция сдвига между аргументами: Kx(t1,t2) = Kx(τ).

Свойства корреляционной функции стационарного процесса:

1. Kx(τ) = Kx(-τ)

2. Kx(0) = Dx

3. | Kx(τ)| ≤ Dx

Эргодическое свойство стационарного с.п.

Рассмотрим стационарный с.п. X(t)

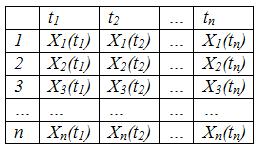
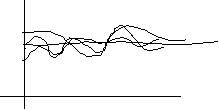На рисунке стационарный процесс и каждая реализация обладает одними и теми же характеристиками. Если мы выберем одну реализацию, то её характеристики будут мало отличаться от характеристик других реализаций. Одна реализация может заменить все остальные. Для эргодического процесса одна из произвольно выбранных реализаций при достаточно большом времени может дать достаточно хорошее представление о всем процессе.

Стационарные процессы могут обладать или не обладать эргодическим свойством. При рассмотрении Марковских процессов с дискретными состояниями мы вводили понятие эргодического множества состояний. Если процесс протекает однородно и множество состояний конечно и обладает эргодическим свойством, то в нем устанавливается стационарный режим функционирования, характеризующийся тем, что любая реализация этого процесса рано или поздно пройдет через любое состояние независимо от того, в каком состоянии находился этот процесс в начальный мом ент времени. Другими словами, эргодическое свойство состоит в том, что любая реализация эргодического стационарного с.п.  достаточной продолжительности пройдет через любое состояние данного процесса, независимо от того в каком состоянии процесс находился в начальный момент времени.

Стационарный процесс обладает свойством эргодичности, если его характеристики найденные усреднением множества реализаций совпадают с соответствующими характеристиками, полученными усреднением по времени одной реализации на достаточно большом интервале. Матожидание: 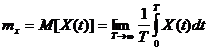                     Достаточным условием эргодичности с.п. X(t) по математическому ожиданию - является условие :  Дисперсия: 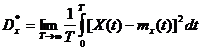                           Достаточным условием эргодичности с.п. X(t) по дисперсии - является условие :   , где Ky(τ) – корреляционная функция с.п. Y(t) = [X(t)]2. 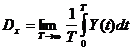Корреляционная функция:  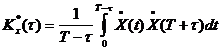, нахождение корреляции усреднением по времени. 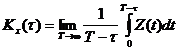 , если выполняется данное условие, то такой с.п. называется эргодичным относительно корреляционной функции.

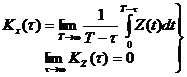 достаточное условие эргодичности по к.ф.

Обычно стационарный с.п. бывает неэргодическим, когда он протекает неоднородно. В частности неэргодичность с.п. X(t) может быть вызвана тем, что в качестве слагаемого с.п. рассматривается с.в. Например, случайный процесс Y(t) = X(t) + U будет неэргодическим.

Характеристики: my(t) = mx + mu Ky(τ) =Kx(τ) + Du