Основные понятия и краткие сведения из теории вероятностей

Случайные события- события, которые в результате произведенного опыта могут произойти или не произойти. Обозначим случайное число символом А.

Достоверное событие – такое событие, которое непременно должно произойти. Обозначим достоверное событие символом е.

Невозможное событие- такое событие, которое заведомо не может произойти. Обозначим невозможное событие символом U.

Совместные (несовместные) события- такие события, появление одного из которых не исключает (исключает) возможность появления другого события.

Зависимые (независимые) события- такие события, появление одного из которых влияет (не влияет) на появление другого события.

Противоположное событие относительно некоторого выбраннго события А- событие, состоящее в непоявлении этого выбранного события. Обозначим противоположное событие .

Полная группа событий- такая совокупность событий, что в результате опыта обязательно должно произойти хотя бы одно из событий этой совокупности.

П р и м е ч а н и е. События A и составляют полную группу событий, так как в результате опыта возможны только два исхода: либо событие А произойдет, либо не произойдет (т. е. произойдет событие ) .

Сумма событий A , A , … , A - такое событие А, появление которого в опыте эквивалентно появлению в том же опыте хотя бы одного любого из событий А , А , …, А . Обозначим сумму событий как

Произведение событий А , А , …, А - такое событие А, появление которого в опыте эквивалентно появлению в том же опыте всех событий А , А , …, А одновременно. Обозначим произведение событий как

А=А А … А = А . (1)

Случайная величина- переменная величина, которая в результате опыта может принимать то или иное значение.

Дискретная случайная величина – такая случайная величина, которая может принимать лишь конечное или счетное множество значений.

Непрерывная случайная величина – такая случайная величина, которая может принимать любое значение в определенном (возможно, бесконечном) интервале.

Случайный процесс – совокупность случайных величин, зависящих от некоторого параметра (например, от времени).

Вероятность случайного события – (классическое определение).

Рассмотрим равновозможные события А , А , …, А , т. е. такие события, при которых не существует никаких объективных причин для более частого появления любого из них. (Предполагается, что все эти события независимые и несовместимые и составляют полную группу событий.) Такие события называют элементарными. Пусть интересующее нас событие А может быть разделено на некоторое число k элементарных событий А , А , …, А , т. е. появление одного любого из элементарных событий эквивалентно наступлению события А. Вероятностью события А называется отношение числа k благоприятных^ исходов к общему числу m всех элементарных исходов:

Р (А)= . (2)

Основные свойства вероятности. Вероятности случайных событий обладают следующими основными свойствами:

Р(U)=0,

P(E)=1, (3)

0=P(U) P(A) P(E)=1,

P(A)+P( )=1.

Теорема сложения вероятностей. Если A , A , … , A - несовместимые события и А есть сумма этихсобытий, то вероятность события А равняется сумме вероятностей события A , A , … , A , т. е.

P(A)=P 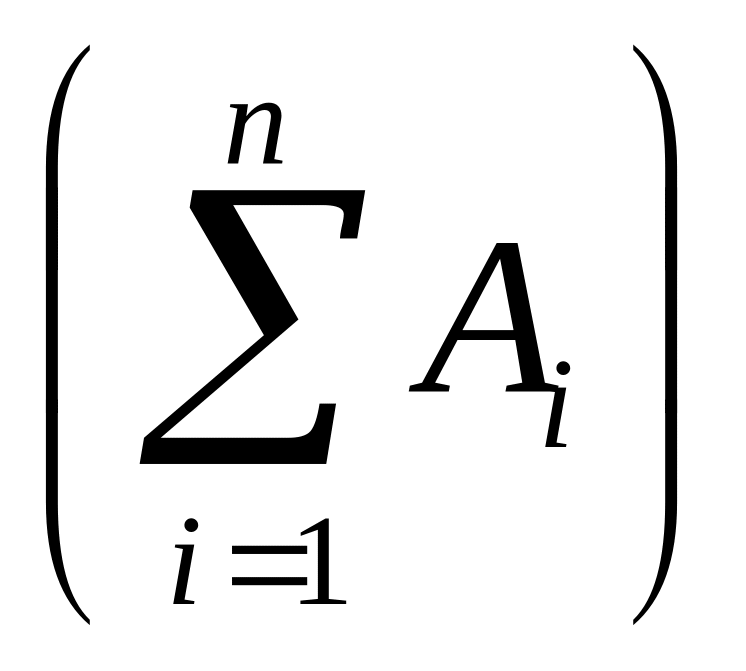= P(A ) + P(A ) +… + P(A )= P(A ). (4)

Следствие 1. Если несовместимые случайные события A , A , … , A составляют полную группу событий то

P = P(E)=1. (5)

Следствие 2. Для любых случайных событий А и А имеет место

P(A A ) + P(A ) = P(A ). (6)

Действительно,

P(A A ) + P(A ) = P(A A + A ) = P(A (A + ) = P(A + E)=

= P(A )P(E)= P(A ).

Условная вероятность события А при наступлении события А - вероятность события А , вычисленная в предположении, что событие А наступило. Обозначим эту условную вероятность Р(А | А ):

Р(А | А ) = . (7)

Следствие 3. Из определения следует, что для независимых событий А и А

Р(А | А ) = Р(А ) и Р(А | А ) = Р(А ).

Теорема умножения вероятностей. Вероятность совместного появления двух событий А и А в данном опыте равняется вероятности одного из них, умножен

Р(А А ) = Р(А | А ) Р(А ). (8)

Р(А А … А )= Р(А | А … А )×

× Р(А | А … А )× Р(А | А … А ) Р(А ). (9)

Следствие 4. В формуле (8), поменяв местами А и А получим

Р(А А ) = Р(А | А ) Р(А ),

т. е.

Р(А )Р(А | А )= Р(А ) Р(А | А ) (10)

Теорема умножения вероятностей для независимых событий.

Р(A , A , … , A )=Р( )=

= Р(A ) Р( A ) … Р( A )= . (11)

Следствие 5.

Р(А А ) = Р(U)= 0 (12)

Следствие 6.

Р(А А )> Р(А А ) Р(А А ) >0. (13)

Р(А ), Р( А ) >0.

Теорема сложения для совместных случайных событий.

Р(А + А )= Р(А )+ Р( А )- Р(А А ). (14)

Для n совместных случайных событий формула сложения вероятностей (14) имеет вид

Р( )= - Р(А А ) + … + ( -1 ) Р( ). (15)

Формула полной вероятности является обобщения формул умножения и сложения вероятностей. Если событие А может осуществиться лишь при условии, что произошло какое-нибудь событие из числа несовместимых событий , вероятности которых известны, и если известны условные вероятности Р(А | А ) (для всех i= 1, 2, …, n), то вероятность события P(A ) может быть вычислена по формуле полной вероятности

Р(А )= Р(А )Р(А | А ) (16)

Действительно,

А = (А А ).

На основании правила сложения вероятностей имеем

Р(А )=Р =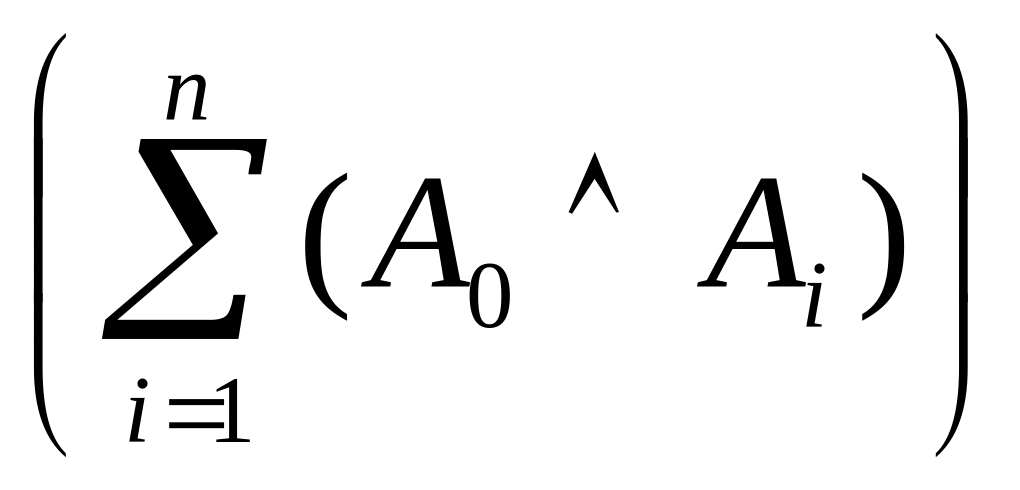

и далее, на основании правила умножения вероятностей каждое из слагаемых представляем в виде

Р(А А )=Р(А ) Р(А | А ),

откуда окончательно получаем

Р(А)= Р(А ) Р(А | А ).

Обычно события А , А , … , А , при которых только и может наступить событие А , называют гипотезами относительно А .

Формула вероятностей гипотез (формула Байеса). Пусть А , А , … , А являются несовместимыми гипотезами относительно события А . Условная вероятность гипотезы А , вычисленная в предположении, что событие А имело место, определяется по формуле

Р(А | А )=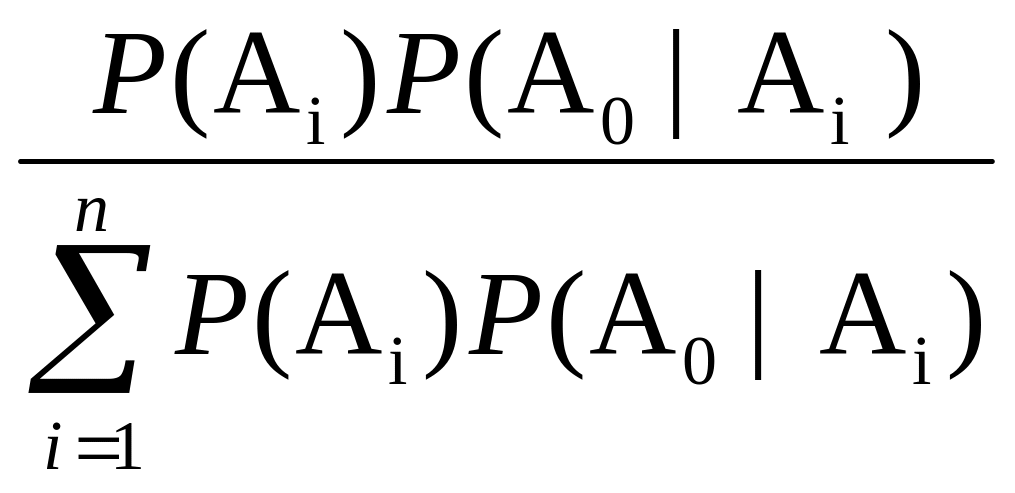 . (17)

Функция распределения (интегральная функция распределения случайной величины^) – вероятность события , где х- переменная величина:

F(x)= . (18)

Следствие 7. Из определения функции распределения следует, что

F(- )= 0,

F(+ )= 1, (19)

0 F(x) 1.

Следствие 8. Из определения функции распределения следует, что

х    х = F(x )- F(x . (20)

Следствие 9. Если некоторая дискретная случайная величина с вероятностью р принимает определенное значение  из конечного числа n возможных значений  ,  , …,  , то функция распределения может быть записана в виде

F(x)=

x ,

 ,

 x

 , (21)

 ,

 ,

xx .

П р и м е ч а н и е. Если число возможных значений n= 1, т. е. величина может принять одно и только одно значение с, то такая величина называется регулярной или неслучайной. Функцию распределения такой величины можно записать следующим образом:

F(x)= (22)

Плотность распределения случайной величины (дифференциальная функция распределения, плотность вероятности) – предел отношения вероятности того, что случайная величина  при испытании примет значение, лежащее в интервале [ x, + x ], к величине интервала x, когда x 0:

f(x)= . (23)

Иными словами, плотность распределения есть первая производная от интегральной функции распределения

f(x) = F(x)= F (x) (24)

Следствие 10. Из определения плотности распределения (21) и следствия 8 вытекает^

= . (25)

Условной плотностью распределения случайной величины в точке x будем называть плотность распределения, вычисленную при условии, что случайная величина больше, чем x, - x , при x 0.

(x)= . (26)

П р и м е ч а н и е. Ясно, что могут быть определены условные плотности распределения и для других условий, однако в теории надежности именно подобная условная плотность наиболее важна.

Математическое ожидание (среднее значение) случайной величины определяется:

а) для дискретных случайных величин

M(x)= , (27)

б) для непрерывных случайных величин

M(x)= , (28)

в) для неотрицательных случайных величин

M(x)= , (29)

если интеграл (29) существует.

П р и м е ч а н и е. Математическое ожидание часто называют начальным моментом первого порядка для распределения F(x). Начальный момент n-го порядка определяется величиной

M (x)= .

Следствие 11. Из формул (22) и (29) имеем

M(c)= c (30)

Следствие 12. Из правила вынесения постоянной за знак интеграла следует

M(cx)= cM(x) (31)

Следствие 13. Из правила об интеграле сумма любых случайных величин определяется

M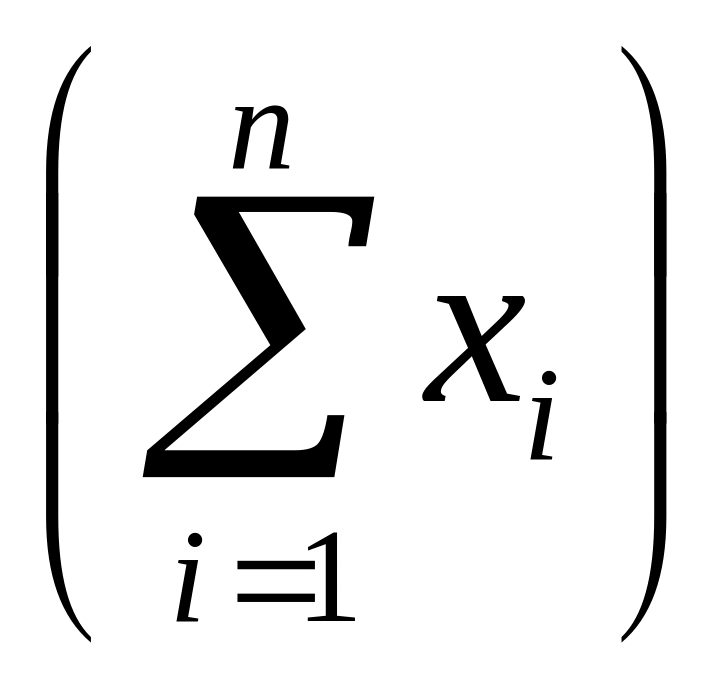 = . (32)

Следствие 14. Из следствий 11 и 13 вытекает

M(c+x)=c + M(x). (33)

Следствие 15. Для независимых случайных величин из правила разделения независимых переменных в n-кратных интегралах следует

M . (34)

Дисперсия случайной величины- величина, определяемая по формулам:

D(x)= M(x-M(x)) (35)

или

D(x)= M(x ) – (M(x)) (36)

а) для дискретных случайных величин

D(x)= (37)

или

D(x)= 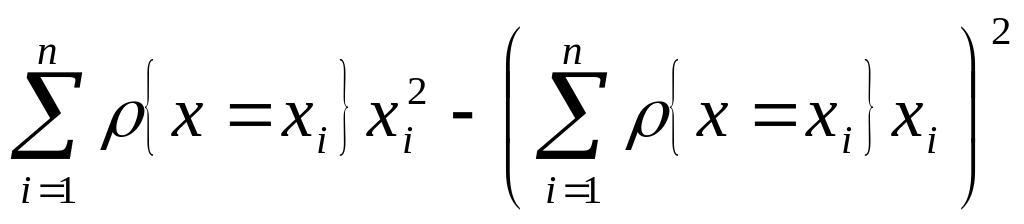, (38)

б) для непрерывных случайных величин

D(x)= (39)

или

D(x)= . (40)

П р и м е ч а н и е. дисперсию часто называют моментом второго порядка для распределения F(x).

Следствие 16. Из определения дисперсии и (30) вытекает

D(c)=0. (41)

Следствие 17. Из (35) и (31) имеем

D(cx)=c D(x). (42)

Следствие 18. Из (37) и (43) следует

D(c+x)=D(x). (43)

Следствие 19. Для суммы независимых случайных величин

D . (44)

Среднее квадратическое (стандартное) отклонение – величина, определяемая по формуле

. (45)