Условные вероятности

На практике случайные события обычно взаимосвязаны. Информация о наступлении одного из событий может влиять на шансы наступления другого. Пусть - конечное пространство равновозможных исходов, А и В – некоторые события. Если о событии В ничего неизвестно, то согласно классическому определению вероятности:

.

Если же известно, что событие В уже произошло (т. е. наступил исход , но какой именно – неизвестно), то для определения вероятности события А следует выбрать новое пространство элементарных событий .

В этом случае событию А благоприятствуют исходы и новая вероятность, которую обозначим оказывается равна:

.

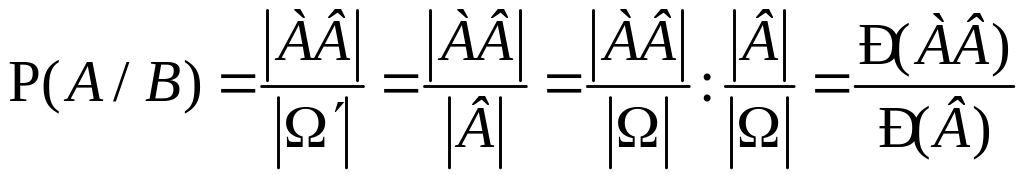Полученная вероятность называется условной вероятностью события А при условии, что событие В произошло и полученное для нее выражение в рамках классической схемы принимается за определение условной вероятности и в общем случае.

Определение. Пусть А и В некоторые случайные события, . Условной вероятностью события А при условии, что событие В произошло, называется величина

.

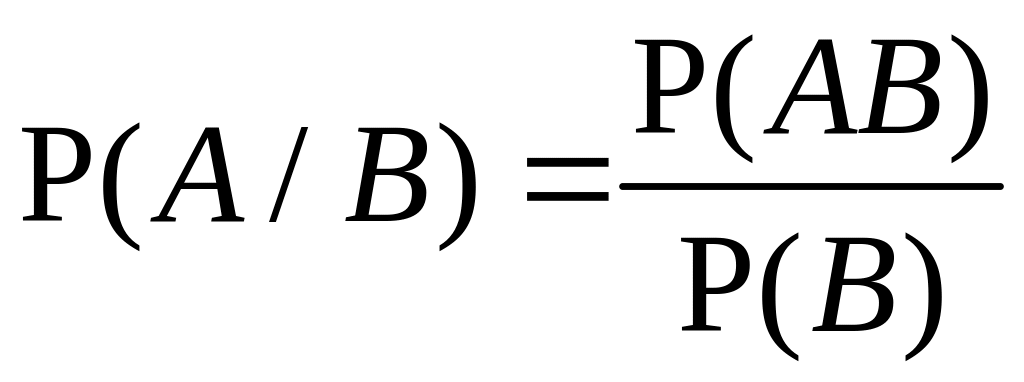Для условной вероятности применяется также обозначение .

Условная вероятность , как функция события А при фиксированном событии В (условии), удовлетворяет аксиомам 1° – 3° и, следовательно, всем свойствам вероятности, вытекающим из аксиом:

.

(Действительно, ).

(Действительно, ,

поскольку события являются несовместными).

Аналогично вводится понятие условной вероятности события В при условии, что событие А произошло:

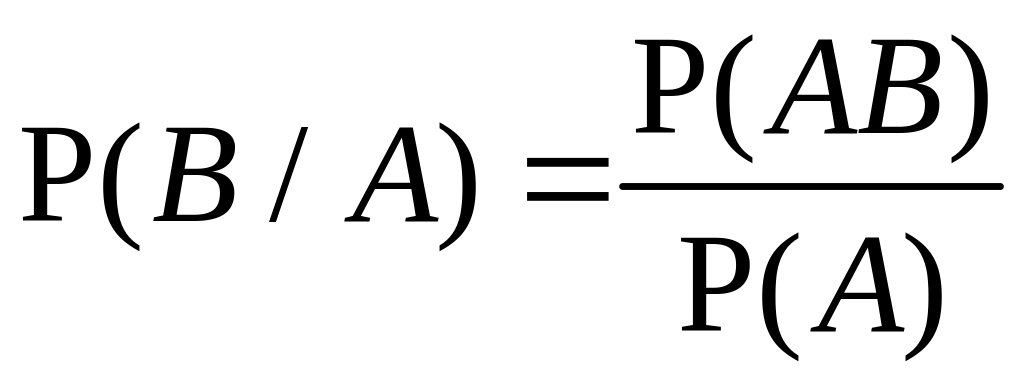
в предположении, что .

Если и , то из определения условных вероятностей и получаем следующее правило умножения вероятностей:

.

На случай любого конечного числа событий правило умножения вероятностей обобщается следующим образом.

Теорема (умножения вероятностей).

Пусть  некоторые события, для которых . Тогда

.

▲ В соответствии с правилом умножения вероятностей

. ■

Пример.

Партия из 100 деталей содержит 5 бракованных. Найти вероятность того, что среди отобранных 10 деталей не будет бракованных.

Решение. Рассмотрим события

;

.

Тогда и в соответствии с теоремой умножения вероятностей получаем:

.

Заметим, что тот же ответ получается и при использовании классического определения вероятности:

, и = 0,584 (см. Урновая схема).

Зависимые и независимые события

Зависимость событий понимается в вероятностном смысле, а не в функциональном. Это означает, что по появлению одного из зависимых событий нельзя однозначно судить о появлении другого. Вероятностная зависимость означает, что появление одного из зависимых событий только изменяет вероятность появления другого. Если вероятность не изменяется, то события считаются независимыми.

Определение: Говорят, что событие А не зависит от события В, если его условная вероятность совпадает с безусловной вероятностью :

.

Если событие А зависит от события В, то .

Понятие независимости симметрично, то есть, если событие А не зависит от события В, то и событие В не зависит от события А. Действительно, пусть . Тогда .

Поэтому говорят просто, что события А и В независимы.

Из правила умножения вероятностей вытекает следующее симметричное определение независимости событий.

Определение: События А и В называются независимыми, если

.

Если , то события А и В считаются зависимыми.

Отметим, что данное определение справедливо и в случае, когда или .

Свойства независимых событий.

1. Если события А и В являются независимыми, то независимыми являются также следующие пары событий: .

▲ Докажем, например, независимость событий . Представим событие А в виде: . Поскольку события являются несовместными, то , а в силу независимости событий А и В получаем, что . Отсюда , что и означает независимость . ■

2. Если событие А не зависит от событий В₁ и В₂, которые являются несовместными ( ), то событие А не зависит и от суммы .

▲ Действительно, используя аксиому аддитивности вероятности и независимость события А от событий В₁ и В₂, имеем:

. ■

Связь между понятиями независимости и несовместности.

Пусть А и В  любые события, имеющие ненулевую вероятность: , так что . Если при этом события А и В являются несовместными ( ), то и поэтому равенство не может иметь место никогда. Таким образом, несовместные события являются зависимыми.

Когда рассматривают более двух событий одновременно, то попарная их независимость недостаточно характеризует связь между событиями всей группы. В этом случае вводится понятие независимости в совокупности.

Определение: События называются независимыми в совокупности, если для любого 2  m  n и любой комбинации индексов справедливо равенство:

.

При m = 2 из независимости в совокупности следует попарная независимость событий. Обратное неверно.

Пример. (Бернштейн С.Н.)

Случайный эксперимент заключается в подбрасывании правильного четырехгранника (тетраэдра). Наблюдается грань, выпавшая книзу. Грани тетраэдра окрашены следующим образом: 1 грань - белая, 2 грань - чёрная, 3 грань - красная, 4 грань - содержит все цвета.

Рассмотрим события:

А = {Выпадение белого цвета}; B = {Выпадение черного цвета};

C = {Выпадение красного цвета}.

Тогда ;

.

Следовательно, события А, В и С являются попарно независимыми.

Однако, .

Поэтому события А, В и С независимыми в совокупности не являются.

На практике, как правило, независимость событий не устанавливают, проверяя ее по определению, а наоборот: считают события независимыми из каких-либо внешних соображений или с учетом обстоятельств случайного эксперимента и используют независимость для нахождения вероятностей произведения событий.

Теорема (умножения вероятностей для независимых событий).

Если события являются независимыми в совокупности, то вероятность их произведения равна произведению вероятностей:

.

▲ Доказательство теоремы следует из определения независимости событий в совокупности или из общей теоремы умножения вероятностей с учетом того, что при этом

.■

Пример 1 (типовой пример на нахождение условных вероятностей, независимость событий, теорему сложения вероятностей).

Электрическая схема состоит из трех независимо работающих элементов. Вероятности отказов каждого из элементов соответственно равны .

1 ) Найти вероятность отказа схемы.

2) Известно, что схема отказала.

Какова вероятность того, что при этом отказал:

а) 1-й элемент; б) 3-й элемент?

Решение. Рассмотрим события = {Отказал k-й элемент}, и событие А = {Отказала схема}. Тогда событие А представляется в виде:

.

1) Поскольку события и несовместными не являются, то аксиома аддитивности вероятности 3° неприменима и для нахождения вероятности следует использовать общую теорему сложения вероятностей, в соответствии с которой

.

Используя далее независимость событий , , имеем:

.

2) Если уже известно, что схема отказала, то для нахождения вероятности отказа при этом 1-го элемента необходимо найти условную вероятность . По определению условной вероятности и с учетом того, что , получаем:

.

Поскольку , то условная вероятность находится несколько иначе:

.

Пример 2.

Вероятность попадания в цель при каждом выстреле 0,9. Сколько надо сделать независимых выстрелов, чтобы поразить цель с вероятностью не менее, чем 0,9999?

Решение. Пусть n – число сделанных выстрелов, событие = {Попадание в цель при k-м выстреле}, , событие А = {Поражение цели}. Очевидно, что , но поскольку события , не являются попарно несовместными, то для нахождения вероятности следует использовать теорему сложения вероятностей в общем виде.

Удобнее перейти к противоположному событию и использовать свойство 1 независимых событий:

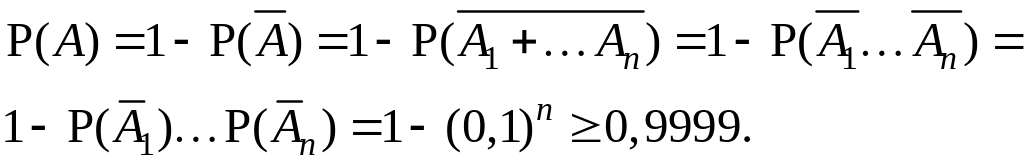
Разрешая полученное неравенство относительно n, получаем, что .