38

Федеральное агентство по образованию

Вологодский государственный технический университет

Кафедра водоснабжения и водоотведения

Гидравлика

ПРИБОРЫ И МЕТОДЫ ИЗМЕРЕНИЯ ГИДРАВЛИЧЕСКИХ ВЕЛИЧИН

Методическое пособие к лабораторным занятиям и для самостоятельной работы студентов

Факультет экологии

Специальности: 270112, 270205, 270102, 270105, 280402, 280302, 190601

Вологда

2008

УДК 621.22.01

Гидравлика. Приборы и методы измерения гидравлических величин: Методическое пособие к лабораторным занятиям и для самостоятельной работы студентов. Вологда: ВоГТУ, 2008. – 38 с.

Методическое пособие предназначено для студентов очной и заочной форм обучения специальностей 270112, 270205, 270102, 270105, 280402, 280302, 190601 по курсу гидравлика, знакомит с основами устройства и принципами действия приборов для измерения гидравлических параметров и способами обработки результатов экспериментов, которые проводятся в рамках лабораторного курса

Утверждено редакционно-издательским советом ВоГТУ

Составители: Нешатаева А.В., канд. техн. наук, доцент

Тянин А.Н., канд. техн. наук, доцент

Рецензент: Одинцов В.В., канд. техн. наук, доцент

ВВЕДЕНИЕ

Методическое пособие предназначено для студентов очной и заочной форм обучения специальностей 270112, 270205, 270102, 270105, 280402, 280302, 190601, знакомит с основами устройства и принципами действия приборов для измерения гидравлических параметров и способами обработки результатов экспериментов, которые проводятся в рамках лабораторного курса.

1. Оценка погрешности измерений в экспериментах

В условиях лабораторий экспериментальным путем получают численные значения гидравлических характеристик. Одни величины получают непосредственно по приборам, такие измерения называют прямыми. Другие вычисляют по результатам прямых измерений параметров, связанных известной зависимостью с искомой величиной (косвенные). При любых, даже самых тщательных, опытах возможны ошибки. Различают три основных типа погрешностей: систематические, случайные и грубые.

Под систематическими понимают погрешности, величина которых одинакова во всех измерениях, проводящихся одним и тем же методом с помощью одних и тех же измерительных приборов. Например, если допущена ошибка в градуировке или в установке нуля, систематическая погрешность результатов будет постоянна.

Случайными называются неопределенные по величине погрешности, зависящие от многих факторов. При повторных опытах в одних и тех же условиях они проявляются в разбросе экспериментальных данных. Чаще это результат субъективной ошибки или погрешности прибора. Случайные ошибки нельзя полностью исключить, но можно уменьшить при обработке многократных измерений.

Грубые погрешности являются следствием резкого нарушения условий в отдельном эксперименте (неисправность прибора, неверное снятие отсчетов и др.). Для их выявления и исключения применяют специальные критерии.

При оценке ошибки измерений используют понятия абсолютной и относительной погрешности. Абсолютная погрешность представляет собой разность результата каждого измерения и истинного значения измеряемой величины X. Она может быть положительной и отрицательной:

(1.1)

Качество результатов измерений удобно характеризовать не абсолютной величиной ошибки , а ее отношением к измеряемой величине , которое называется относительной погрешностью и обычно выражается в процентах:

(1.2)

Поскольку истинное значение измеряемой величины неизвестно, используют приближенные оценки. При соблюдении нормального закона распределения ошибок за наиболее вероятное значение измеряемой величины принимают среднее арифметическое из п результатов:

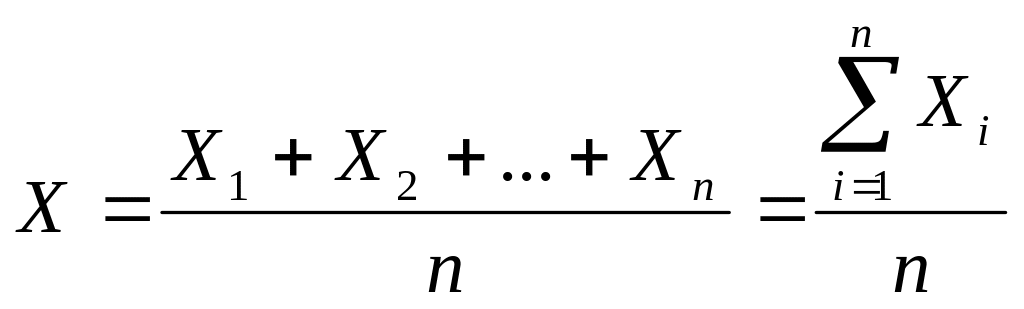(1.3)

Тогда в уравнения (1.1) и (1.2) вместо истинного значения подставляют X.

Численной мерой возможности появления определенного события, например, совпадения истинной величины с измеренной, служит вероятность Р. Вероятность невозможного события Р=0, а абсолютно достоверного Р—1. Обычно 0<Р<1. Методы теории вероятности позволяют определить вероятность того, что истинное значение отличается от среднего на величину, не превышающую , то есть с вероятностью Р находится в интервале

(1.4)

Этот интервал называют доверительным, вероятность Р - доверительной вероятностью, - максимальной абсолютной погрешностью.

Средняя квадратичная погрешность среднего арифметического значения определяется по формуле:

(1.5)

где - результат каждого измерения;

n - число измерений одной и той же величины.

Средняя квадратичная погрешность соответствует вероятности Р=0.68, то есть 68% полученных ошибок не превышают . Если считать, что в пределах максимальной погрешности заключено 95% полученных ошибок (Р=0.95), то . Если Р = 0.997, то .

Для характеристики случайной ошибки нужно определить доверительный интервал (значение ошибки) и доверительную вероятность. При относительно малом числе измерений величины , , Р связывают с помощью коэффициентов Стьюдента, таблицы которых приведены в справочной литературе [1, 2].

Для оценки прямого однократного измерения определяют максимальную погрешность, допустимую классом точности прибора:

(1.6)

где К - класс точности прибора;

N - предельное значение измерительной шкалы.

В рабочих условиях обычно применяют приборы классов 0,5 - 6, которые называют техническими. Приборы классов 0,4 и выше используют как образцовые для поверок и градуировок других приборов и как рабочие для измерений высокой точности.

Средняя квадратичная погрешность прямого однократного измерения определяется по формуле:

(1.7)

При оценке погрешности косвенно измеряемой величины необходимо учитывать погрешности всех прямо измеряемых величин, по которым производят расчеты. Ошибка в результате вычислений должна быть примерно на порядок (то есть в 10 раз) меньше суммарной ошибки измерений.

В лабораторных работах часто требуется сопоставить значение X, найденное в эксперименте, и взятое из справочной литературы. В этом случае рассчитывают их относительное расхождение в %:

(1.8)

При проведении технических расчетов всегда нужно ориентироваться на определенную погрешность результата (в инженерной практике - порядка 5%).