Уравнение для продольных колебаний струны.

Уравнение для продольных колебаний струны, стержня, пружины записывается одинаково. Поэтому обычно вывод записывают только для продольного стержня. Стержень – это тело цилиндрической или другой формы для растяжения или изгиба которого нужно приложить усилие. Это отличает стержня от струны. При выводе уравнения учитывается площадь поперечного сечения S(x) и модуль Юнга k(x).

Где – линейная плотность.

Если все величины будут постоянными, то они будут const.

Делим на const, получаем:

(16)

Получили однородное волновое уравнение, оно совпадает с уравнением (14).

Энергия колебаний струны

Найдём выражение для энергии поперечных колебаний струны , где K – кинетическая и U – потенциальная энергия. Элемент струны dx, движущийся со скоростью , обладает кинетической энергией

Кинетическая энергия всей струны равна

(1)

Потенциальная энергия поперечных колебаний струны, имеющей при форму , равна работе которую надо совершить чтобы струна перешла из положения равновесия в положение . Пусть функция дает профиль струны в момент t,причем

,

Элемент dx под действием равнодействующих сил натяжения

за время dt проходит путь . Работа, производимая всей струной за время dt, равна

Интегрируя по от 0 до , получаем:

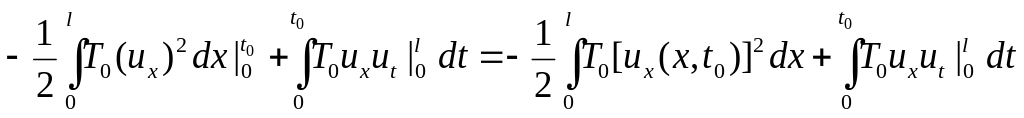
При перемещении закрепленной на концах струны из положения равновесия u=0 в положение работа не зависит от способа перевода струны в это положение и равна

(2)

Потенциальной энергии струны в момент с обратным знаком. Таким образом, полная энергия для поперечных колебаний струны равна:

(3)

Аналогично может быть получено выражение для потенциальной энергии продольных колебаний стержня:

(4)

Малые поперечные колебания мембраны

Мембраной называется плоская пленка, не сопротивляющаяся изгибу и сдвигу.

Чем будут отличатся малые поперечные колебания струны.

При рассмотрение уравнения для колебаний струны мы имели функцию , зависящую от двух переменных . Для мембраны в уравнение колебания появляется новая пространственная переменная y . Тогда для однородной мембраны двухмерное волновое уравнение запишется в виде:

(1)

3.2.Уравнение для напряженности электрического и магнитного полей в вакууме

При описании поперечных колебаний мембраны мы переходим к двухмерному волновому уравнению (1). К трехмерному волновому уравнению можно перейти при выводе уравнений для напряженности электрического и магнитного полей в вакууме. Система уравнений Максвелла:

Применяя операцию ротора к первому из уравнений Максвелла, получим

, но так как , то мы имеем . Заменим через , в итоге получим трехмерное волновое уравнение:

Введем оператор Даламбера: