Кинетическая энергия вращающегося твердого тела

Начнем с рассмотрения вращения тела вокруг неподвижной оси, проходящей чрез него.

Мысленно разбив тело на элементарные объемыv_i массами m_i, находящиеся на расстоянии r_i от оси, получим, что скорость элементарной массы определяется выражением

v_i = r_i (1)

Следовательно, для кинетической энергии i-той материальной массы получим

Т.к. мы рассматриваем абсолютно твердое тело, то  для всех точек выделенного объема массами m_i будет одинаково, тогда получим

По определению m_ir_i² – момент инерции, получим:

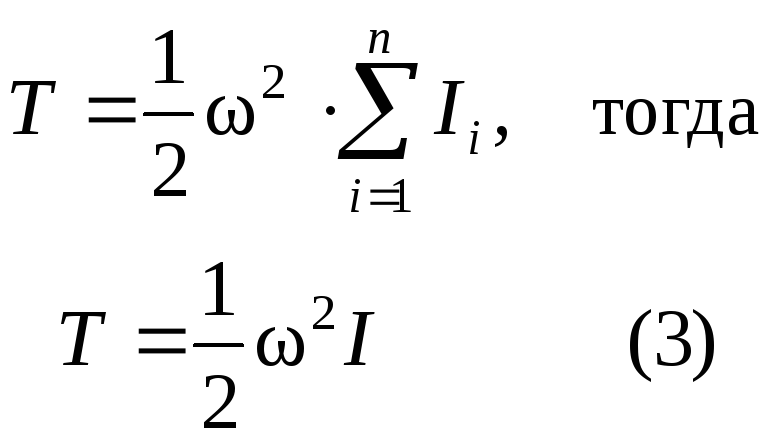
Формула (3) справедлива для тела, вращающегося вокруг неподвижной оси. Плоское движение тела может быть представлено как положение двух движений – поступательного, с некоторой скоростью v₀, и вращения вокруг соответствующей оси с угловой скоростью . Поэтому, произведя некоторые преобразования, получим

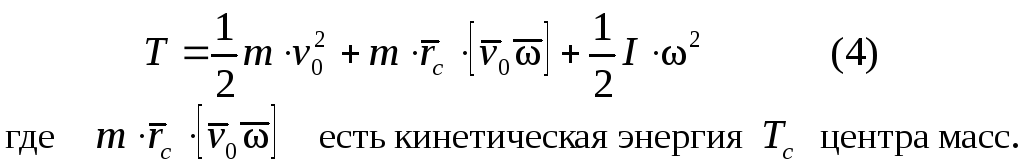
Если ось вращения проходит через центр масс, то r_c = 0, следовательно, равна нулю и кинетическая энергия центра масс.

Обозначим через v_c скорость центра масс, а через I_c момент инерции тела относительно оси, проходящей через центр масс, тогда получим

Формула (5) определяет кинетическую энергию тела при плоском движении, например, цилиндр скатывается по наклонной плоскости.

Момент силы. Уравнение динамики вращательного движения.

О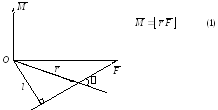ПРЕДЕЛЕНИЕ: Моментом силы M относительно точки O называется физическая величина, численно равная векторному произведению радиус-вектора на силу F.

Вектор M является псевдовектором. Его направление совпадает с направлением поступательного движения правого винта при его вращении от вектора r к вектору F. Модуль момента силы определяется выражением

M = Frsin = Fl (2)

rsin = l – это кратчайшее расстояние между линией действия силы и точкой O. l называется плечом силы.

ОПРЕДЕЛЕНИЕ: Моментом силы относительно неподвижной оси z называется скалярная величина M_z равная проекции вектора M, определенного относительно произвольной точки O данной оси z.

Если ось z совпадает с вектором M момента силы, то M_z находится по формуле

Найдем выражение для работы при вращении тела. Пусть сила F приложена в точке B, находящейся на расстоянии от оси z равном r.

Угол– это угол между направлением силы и радиус-векторомr.

При повороте тела на малый угол d точка приложения B проходит путь

dS = rd,

и работа равна произведению проекции силы на направление смещения на величину этого смещения:

dA = Fsinrd (4)

Согласно формуле (2) получим:

dA = M_zd.

Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота. Т.к. работа идет на увеличение кинетической энергии

тогда получаем M_zd = Id

Продифференцируем обе части по dt:

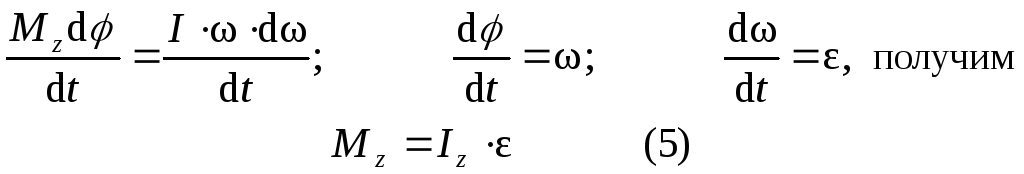
Уравнение (5) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.

Если ось z совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство

МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА.

ОПРЕДЕЛЕНИЕ:Моментом импульса материальной точки Aотносительно неподвижной точкиOназывается физическая величина, численно равная векторному произведению

где вектор r – радиус-вектор, проведенный из точки O в точку A, – импульс тела, векторL – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от вектора r к вектору p.

Модуль момента импульса

L = prsin = pl (2)

где l – плечо вектора p относительно точки O.

ОПРЕДЕЛЕНИЕ: Моментом импульса относительно неподвижной оси z называется скалярная величина L_z равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O указанной оси.

При вращении абсолютно твердого тела вокруг неподвижной оси каждая точка тела движется по окружности радиусом r_i с некоторой скоростью v_i, причем вектор скорости, а следовательно и вектор импульса, перпендикулярны радиус-вектору, т.е. радиус-вектор является плечом вектора импульса и согласно выражению (2)

L_i = m_iv_ir_i (3)

Тогда момент импульса абсолютно твердого тела будет определяться суммой

Зная, что v = r_i, получим

L = r_im_ir_i = m_ir_i² = I.

Получаем: L = I (4)

Продифференцировав выражение (4) по dt, получим:

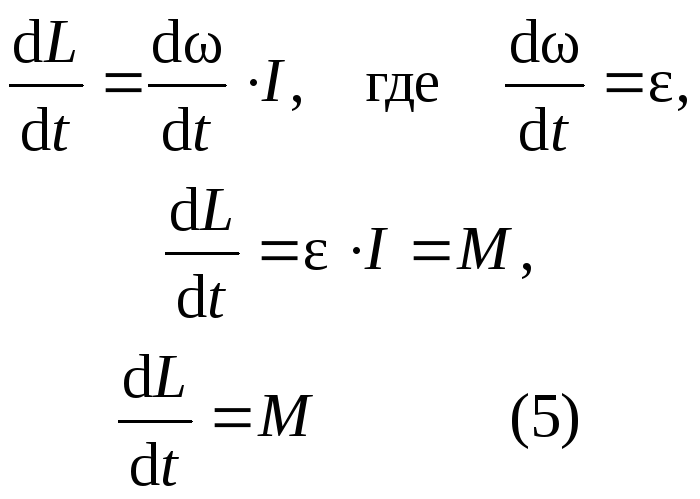
Выражение (5) – еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. В замкнутой системе тел момент внешних сил M = 0, следовательно

Выражение (6) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется со временем.

Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).