Уравнение клапейрона-менделеева.

Состояние некоторой массы газа определяется тремя термодинамическими параметрами P (давление), V (объем) и T (температура). Между этими параметрами существует связь, называемая уравнением состояния, которое в общем виде имеет запись

f(P, V, T) = 0,

где каждая из переменных является функцией двух других.

Французский физик и инженер Клапейрон вывел уравнение состояния идеального газа, объединив законы Бойля-Мариотта и Гей-Люссака.

Пусть некоторая масса газа занимает объем V₁, имеет давление P₁ и находится при температуре T₁. Эта же масса газа в другом состоянии характеризуется параметрами P₂, V₂, T₂.

Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов:

1) изотермического (изотерма 11);

2) изохорического (изохора 12).

В соответствии с законами Бойля-Мариотта и Гей-Люссака

Т.к. состояния 1 и 2 выбраны произвольно, то для данной массы газа выражение

Выражение (3) является уравнением Клапейрона, в котором B – некая газовая постоянная, различная для разных газов.

Менделеев объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (3) к одному молю, использовав при этом молярный объем. Таким образом,

R – это общая для всех газов постоянная, названная молярной газовой постоянной, или универсальной газовой постоянной.

Уравнению

PV_m = RT (4)

удовлетворяет только идеальный газ. Уравнение (4) называется уравнением состояния идеального газа, или уравнением Менделеева-Клапейрона. От уравнения (4) для моля газа можно перейти к уравнению для произвольной массы газа.

Если для заданных P и T моль газа занимает молярный объем, то при тех же условиях масса газа m займет тот же объем.

Тогда получим выражение:

Выражение (5) является уравнением Клапейрона-Менделеева для произвольной массы газа. Если взять

где k – постоянная Больцмана, то получим

Давление идеального газа при данной температуре прямо пропорционально концентрации его молекул. При одинаковых температурах и давлении все газы содержут в единице объема одинаковое число молекул.

ОПРЕДЕЛЕНИЕ: Число молекул, содержащихся в 1 м³ газа, при нормальных условиях называется числом Лошмидта. Оно равно 2,6810²⁵ 1/м³.

Основное уравнение молекулярно-кинетической теории газа.

Рассмотрим одноатомный идеальный газ, предположив, что молекулы движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, удары абсолютно упругие.

Выделим на стенке сосуда некоторую элементарную площадку S.

При каждом соударении молекула, движущаяся перпендикулярно площадке, передает импульс

m₀v – (– m₀v)  = 2m₀v,

где m₀ – масса молекулы, v – ее скорость.

За время t площадки S достигнут только те молекулы, которые заключены в объеме цилиндра с основанием S и высотой vt. Число их равно nSvt, где n – концентрация молекул.

Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлениях так, что в любой момент времени вдоль каждого из них движется ¹/₃ часть всех молекул, причем половина из них движется в одну сторону, а половина – в обратную сторону. Тогда число ударов молекул, движущихся в заданном направлении и ударяющихся о площадку S, будет равно

При столкновении все они передают импульс

Тогда давление газа, оказываемое им на стенку сосуда

Если газ в объеме V содержит N молекул, которые двигаются со скоростями v₁, v₂, …, v_n, то рассматривают среднюю квадратичную скорость

которая характеризует всю совокупность молекул газа, тогда

Выражение (3) – это основное уравнение молекулярно-кинетической теории идеальных газов. Учитывая, что n = N / V, получим

где E – суммарная кинетическая энергия всех молекул. Т.к. масса m = m₀N, то можно записать

Сравним с уравнением Менделеева-Клапейрона, получим:

или, зная, что  = m₀N_A и R = kN_A, получим

Средняя кинетическая энергия поступательного движения одной молекулы идеального газа

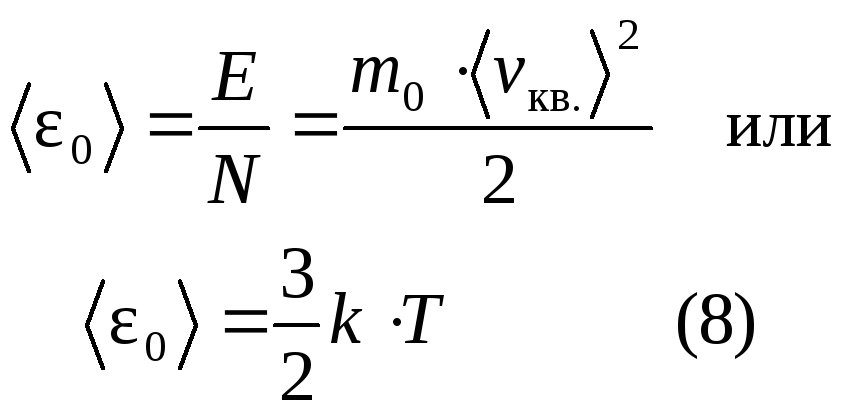
При температуре равной 0 К средняя энергия равна нулю, следовательно давление тоже равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа, и формула (8) раскрывает молекулярно-кинетическое толкование температуры.