
Приклад виконання лабораторної роботи №2
Досліджується залежність продуктивності праці Y (т/год) від рівня механізації робіт Х1 (%), середнього віку робітників Х2 (років) і енергоозброєності Х3 (КВт / 100 працюючих) по даним 14 промислових підприємств (див. таблицю свого варіанту).
Таблиця 1 – Фактори, що впливають на прибуток підприємства
№ п/п |
Продуктивність праці, т/год,
|
Рівень механізації робіт,
%,
|
Середній вік робітників,
років,
|
Енергоозброєність, КВт/100
працюючих,
|
1 |
20 |
32 |
33 |
300 |
2 |
24 |
30 |
31 |
290 |
3 |
28 |
36 |
41 |
350 |
4 |
30 |
40 |
39 |
400 |
5 |
31 |
41 |
46 |
400 |
6 |
33 |
47 |
43 |
480 |
7 |
34 |
56 |
34 |
500 |
8 |
37 |
54 |
38 |
520 |
9 |
38 |
60 |
42 |
590 |
10 |
40 |
55 |
35 |
540 |
11 |
41 |
61 |
39 |
600 |
12 |
43 |
67 |
44 |
700 |
13 |
45 |
69 |
40 |
700 |
14 |
48 |
76 |
41 |
750 |
Рішення
Обчислимо
середні значення та стандартні відхилення
пояснюючих змінних
![]() .
Для цього можна скористатись стандартними
функціями MS Excel (СРЗНАЧ та СТАНДОТКЛ).
.
Для цього можна скористатись стандартними
функціями MS Excel (СРЗНАЧ та СТАНДОТКЛ).
Дані величини можна також розрахувати за формулами:
![]() ,
,
![]() ,
,
де ![]() середнє
значення
середнє
значення
![]() -тої
пояснюючої змінної;
-тої
пояснюючої змінної;
![]() індивідуальне
значення
-тої
пояснюючої змінної;
індивідуальне
значення
-тої
пояснюючої змінної;
![]() стандартне
відхилення
-тої
пояснюючої змінної;
стандартне
відхилення
-тої
пояснюючої змінної;
![]() – число
спостережень.
– число
спостережень.
Додаткові розрахунки наведено в таблиці 1.
Таблиця 1 – Проміжні розрахунки
№ п/п |
|
|
|
|
|
|
|
1 |
20 |
32 |
33 |
300 |
388,65 |
36,00 |
43502,04 |
2 |
24 |
30 |
31 |
290 |
471,51 |
64,00 |
47773,47 |
3 |
28 |
36 |
41 |
350 |
246,94 |
4,00 |
25144,90 |
4 |
30 |
40 |
39 |
400 |
137,22 |
0,00 |
11787,76 |
5 |
31 |
41 |
46 |
400 |
114,80 |
49,00 |
11787,76 |
6 |
33 |
47 |
43 |
480 |
22,22 |
16,00 |
816,33 |
7 |
34 |
56 |
34 |
500 |
18,37 |
25,00 |
73,47 |
8 |
37 |
54 |
38 |
520 |
5,22 |
1,00 |
130,61 |
9 |
38 |
60 |
42 |
590 |
68,65 |
9,00 |
6630,61 |
10 |
40 |
55 |
35 |
540 |
10,80 |
16,00 |
987,76 |
11 |
41 |
61 |
39 |
600 |
86,22 |
0,00 |
8359,18 |
12 |
43 |
67 |
44 |
700 |
233,65 |
25,00 |
36644,90 |
13 |
45 |
69 |
40 |
700 |
298,80 |
1,00 |
36644,90 |
14 |
48 |
76 |
41 |
750 |
589,80 |
4,00 |
58287,76 |
Сума |
492,00 |
724,00 |
546,00 |
7120,00 |
2692,86 |
250,00 |
288571,43 |
Середнє |
35,14 |
51,71 |
39,00 |
508,57 |
192,35 |
17,86 |
20612,24 |
|
8,08 |
14,39 |
4,39 |
148,99 |
— |
— |
— |
|
65,21 |
207,14 |
19,23 |
22197,80 |
— |
— |
— |
За
алгоритмом методу Фаррара-Глобера
перший крок це нормалізація значень
факторів. Нормалізуємо
![]() ,
використавши наведену нижче формулу.
,
використавши наведену нижче формулу.
![]()

|
|
|
|
-0,366 |
-0,366 |
-0,374 |
|
-0,403 |
-0,488 |
-0,392 |
|
-0,292 |
0,122 |
-0,284 |
|
-0,218 |
0,000 |
-0,195 |
|
-0,199 |
0,427 |
-0,195 |
|
-0,088 |
0,244 |
-0,051 |
|
0,080 |
-0,305 |
-0,015 |
|
0,042 |
-0,061 |
0,021 |
|
0,154 |
0,183 |
0,146 |
|
0,061 |
-0,244 |
0,056 |
|
0,172 |
0,000 |
0,164 |
|
0,284 |
0,305 |
0,343 |
|
0,321 |
0,061 |
0,343 |
|
0,451 |
0,122 |
0,433 |
Другим кроком є розрахунок кореляційної матриці R за формулою:
 ,
,
де ![]() –транспонована матриця Х*
(елементи матриці R
характеризують щільність зв’язку
однієї незалежної змінної з іншою);
–транспонована матриця Х*
(елементи матриці R
характеризують щільність зв’язку
однієї незалежної змінної з іншою);
![]() – парні
коефіцієнти кореляції.
– парні
коефіцієнти кореляції.
Транспонуємо
матрицю
![]() (нормалізовану)
в матрицю
(нормалізовану)
в матрицю
![]()
= |
-0,37 |
-0,40 |
-0,29 |
-0,22 |
-0,20 |
-0,09 |
0,08 |
0,04 |
0,15 |
0,06 |
0,17 |
0,28 |
0,32 |
0,45 |
-0,37 |
-0,37 |
-0,49 |
0,12 |
0,00 |
0,43 |
0,24 |
-0,30 |
-0,06 |
0,18 |
-0,24 |
0,00 |
0,30 |
0,06 |
0,12 |
-0,37 |
|
-0,37 |
-0,39 |
-0,28 |
-0,19 |
-0,19 |
-0,05 |
-0,02 |
0,02 |
0,15 |
0,06 |
0,16 |
0,34 |
0,34 |
0,43 |
-0,37 |
Тоді, перемноживши матриці Х* та , отримаємо:
|
0,93 |
0,34 |
0,92 |
R = |
0,34 |
0,93 |
0,39 |
|
0,92 |
0,39 |
0,93 |
Як бачимо, діагональні елементи матриці R не дорівнюють одиниці, отже необхідно штучно проставити на діагоналі матриці одиниці, а до решти елементів додати різницю між одиницею й значенням діагонального елемента.
|
1 |
0,41 |
0,99 |
R = |
0,41 |
1 |
0,46 |
|
0,99 |
0,46 |
1 |
Визначаємо
значення
![]()
![]()
де ![]() – визначник кореляційної матриці R.
– визначник кореляційної матриці R.
Перш за
все визначимо визначник кореляційної
матриці, для чого необхідно
серед математичних функцій MS Excel знайти
функцію “МОПРЕД”. Скориставшись нею,
дістанемо:
![]() .
.
Оскільки наближається до нуля, то в масиві пояснюючих змінних може існувати мультиколінеарність.
Прологарифмуємо
визначник матриці R:
![]() = -4,6225.
= -4,6225.
Тоді
![]()
Порівнюємо
з табличним значенням при
![]() ступенях свободи і рівні значущості α
= 0,05.
Так як
ступенях свободи і рівні значущості α
= 0,05.
Так як
![]() ,
то в масиві незалежних змінних (рівень
механізації, середній вік робітників,
енергоозброєність) існує мультиколінеарність.
,
то в масиві незалежних змінних (рівень
механізації, середній вік робітників,
енергоозброєність) існує мультиколінеарність.
Для
визначення
![]() критеріїв
необхідно знайти матрицю похибок
критеріїв
необхідно знайти матрицю похибок
![]() ,
яка є оберненою до матриці R:
,
яка є оберненою до матриці R:
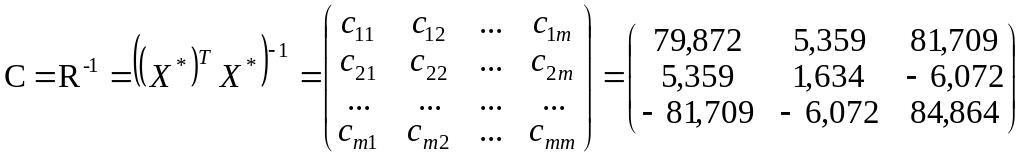
Безпосередньо критерій обчислюється за формулою:
![]()
де ![]() – діагональні елементи матриці С;
– діагональні елементи матриці С;
![]()
![]()
![]()
Обчислені
критерії порівнюються з табличним
значенням при
п’ятивідсотковому рівні значимості і
ступенях свободи
![]() і
і
![]() ,
що складає
,
що складає
![]() .
.
У
розглядуваному випадку
![]() ,
,
![]() ,
,
![]() .
Це означає, що перша і третя змінні
мультиколінеарні з іншими.
.
Це означає, що перша і третя змінні
мультиколінеарні з іншими.
Розрахуємо часткові коефіцієнти кореляції, які характеризують щільність зв’язку між двома змінними за умови, що інші змінні не впливають на цей зв’язок (існування парної мультиколінеарності):
![]()
де ![]() – елементи матриці С,
що розміщені в k-ому
рядку та j-му
стовпці;
– елементи матриці С,
що розміщені в k-ому
рядку та j-му
стовпці;
і
![]() – діагональні елементи матриці С.
– діагональні елементи матриці С.
![]()
![]()
![]()
Отже, спираючись на здобуті нами значення окремих (часткових) коефіцієнтів кореляції, можна сказати, що зв’язок між рівнем механізації та середнім віком робітників є помірним, якщо не враховувати вплив енергоозброєності, зв’язок між рівнем механізації та енергоозброєністю є досить високим, якщо не брати до уваги вплив середнього віку робітників. Зв’язок між середнім віком робітників та енергоозброєністю є середнім, якщо не враховувати рівень механізації.
Визначимо
![]() критерій.
критерій.
Ці критерії застосовуються для визначення мультиколінеарності двох пояснюючих змінних і обчислюються за формулою:
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Обчислені
![]() критерії
порівнюються з табличним значенням
критерії
порівнюються з табличним значенням
![]() при рівні значимості
при рівні значимості
![]() та числі ступенів свободи
та числі ступенів свободи
![]() .
.
Оскільки
![]() ,
то рівень механізації та середній вік
робітників не є мультиколінеарними між
собою;
,
то рівень механізації та середній вік
робітників не є мультиколінеарними між
собою;
![]() ,
тому відповідно рівень механізації та
енергоозброєність є мультиколінеарними
між собою;
,
тому відповідно рівень механізації та
енергоозброєність є мультиколінеарними
між собою;
![]() ,
тому середній вік робітників та
енергоозброєність не є мультиколінеарними
між собою.
,
тому середній вік робітників та
енергоозброєність не є мультиколінеарними
між собою.
Висновок. Дослідження, проведені за алгоритмом Фаррара-Глобера показали, що мультиколінеарність між пояснюючими змінними даного прикладу існує. Отже, для того, щоб можна було застосувати метод 1МНК для оцінювання параметрів моделі за цією інформацію, необхідно в першу чергу звільнитися від мультиколінеарності. Приймаємо рішення про виключення фактору Х3 з подальших досліджень.
