Элементарные функции комплексного переменного.

Рассмотрим некоторые элементарные функции комплексного переменного, а именно, показательную функцию , логарифмическую функцию , тригонометрические - , , , и, обратные тригонометрические функции , , , ,а также гиперболические функции , , , и обратные к ним функции , , , ).

1. Показательная функция комплексного переменного.

Показательная функция определяется как

или (12)

Очевидны следующие свойства функции .

1) ;

2) .

Так как , то показательная функция - периодическая функция периода .

Пример 24. Найти значение функции в точке и указать координаты точки комплексной плоскости, соответствующей найденному значению.

Решение. 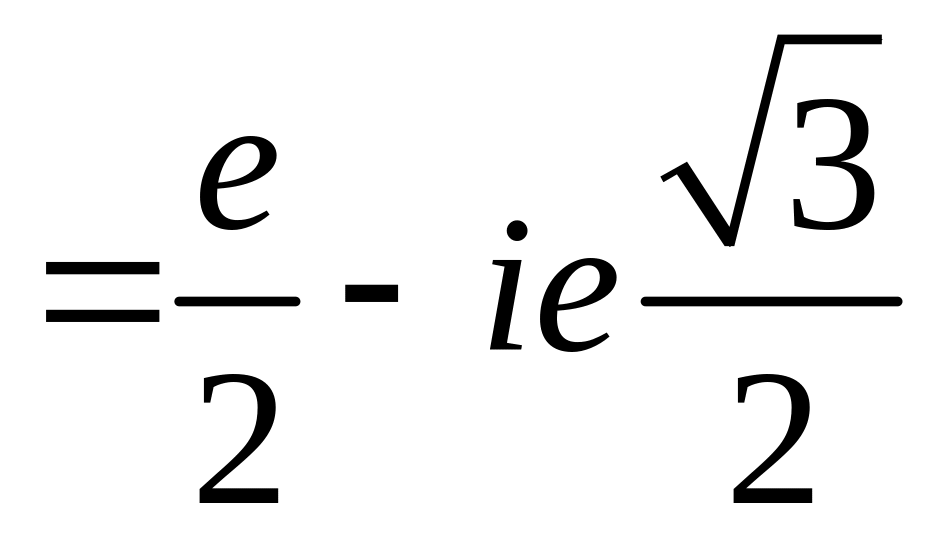, откуда координаты искомой точки .●

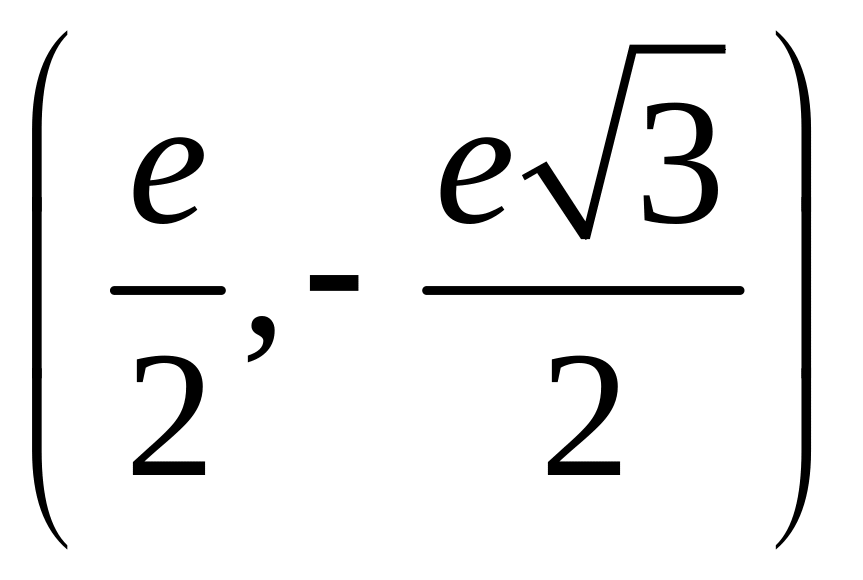2. Логарифмическая функция комплексного переменного.

Логарифмическая функция определяется как обратная к показательной.

Определение. Натуральным логарифмом ( ) комплексного числа называется показатель степени , в которую необходимо возвести число , чтобы получить число .

Пусть , , где .

Тогда , откуда , , , , .

, где (13)

Определение. Выражение называется главным значением натурального логарифма числа .

Из формулы (13) следует, что действительная часть натурального логарифма определяется однозначно, а мнимая часть содержит неопределенное слагаемое, кратное , т. е. существует бесконечное множество значений натурального логарифма любого числа , отличного от нуля. Логарифм нуля не существует.

Пример 25. Вычислить и .

Решение. Найдем модуль и аргумент числа .

. Так как действительная и мнимая части числа отрицательны, то главное значение аргумента равно .

Тогда 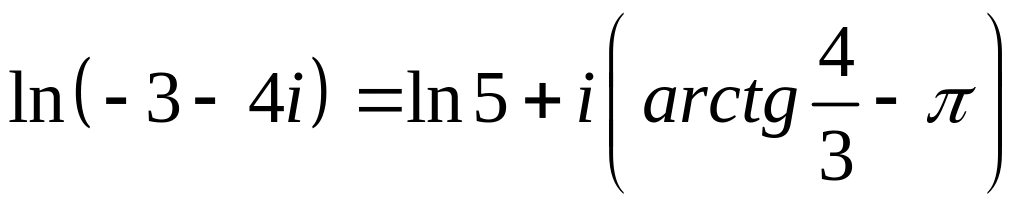- главное значение логарифма данного числа и .●

Пример 26. Вычислить и .

Решение. Модуль числа равен , а главное значение аргумента равно , следовательно, , .●

С помощью логарифма может быть определена любая степень комплексного числа.

Пример 27. Вычислить .

Решение. ,

где .

Обратите внимание, что -действительные числа.●

3. Тригонометрические функции комплексного переменного.

Тригонометрические функции синус и косинус определены ранее (см. формулы (6)).

Определение. Тригонометрическая функция синус комплексного переменного определяется как , где

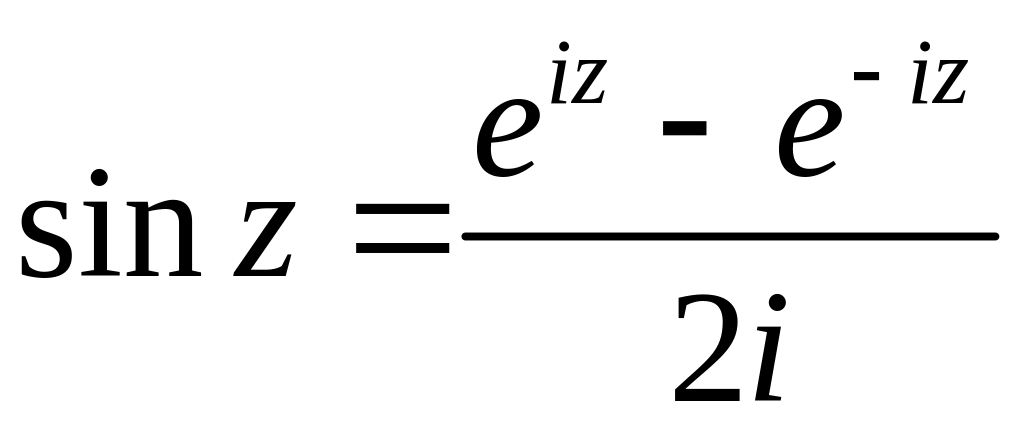, (14)

функция косинус как , где

, (15)

функция тангенс как , где

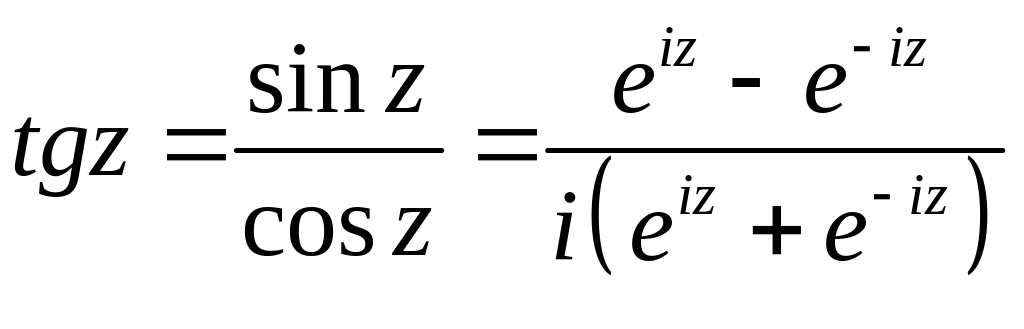, (16)

функция котангенс как , где

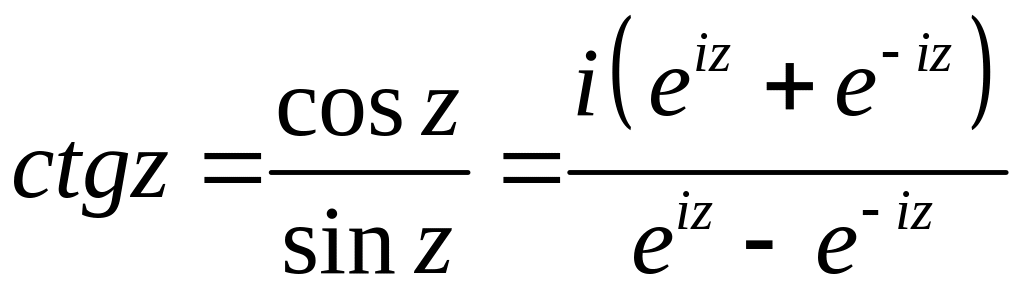. (17)

Пример 28. Вычислить .

Решение. .●

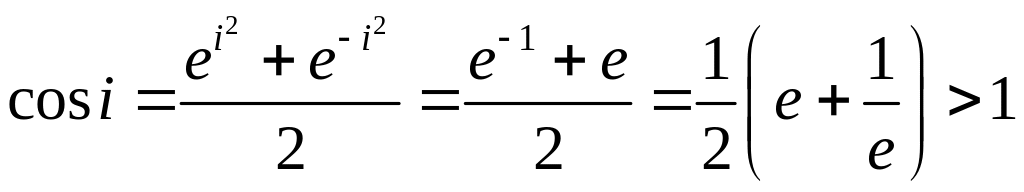Пример 29. Вычислить . Пример 28. Вычислить .

Решение. ●

Пример 30. Доказать, что .

Решение. .●

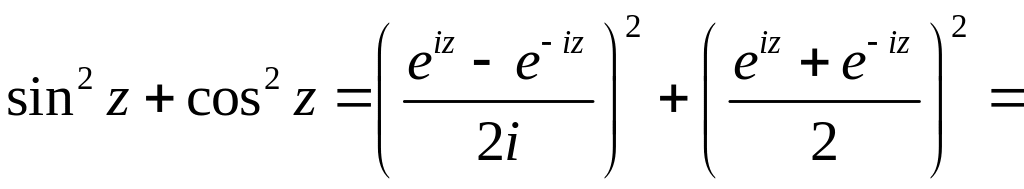
Замечание. Для тригонометрических функций комплексной переменной имеют место и другие тождества, справедливые для тригонометрических функций действительного аргумента (см. пример 31).

Пример 31. Доказать, что .

Решение.

.

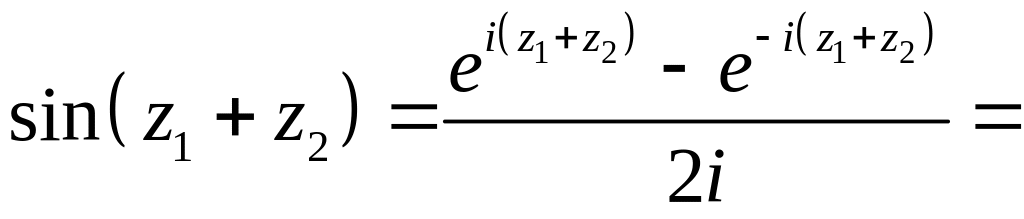
Пример 32. Решить уравнение .

Решение. , откуда 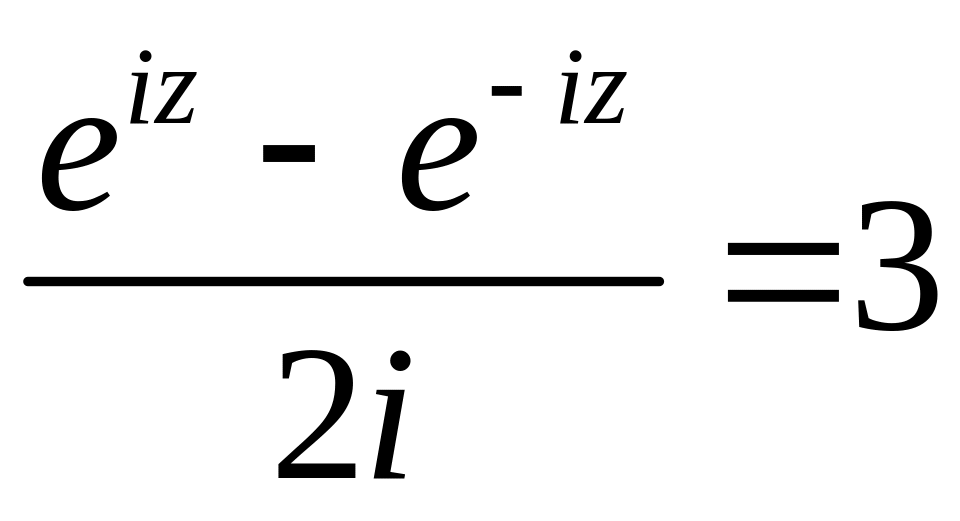, и .

Решая квадратное относительно , имеем или , откуда и .

Ответ:

Замечание. Числа при имеют одинаковые мнимые части, поэтому они лежат на прямой, параллельной действительной оси и отстоящей от нее на расстоянии .●