14

3. Рекуррентные последовательности

Говорят, что элементы u₁, u₂, ..., u_n, образуют рекуррентную последовательность k-го порядка, если заданы первые k членов последовательности u₁, u₂, ..., u_k, а для n > k

u_n = F ( u_n-1, u_n-2, ... , u_n-k ),

где F некоторая функция k аргументов.

1. Т.е. значение n-го элемента может быть вычислено по k предыдущим элементам. Предыдущие значения функции запоминаются в буфере t (см. рисунок ниже).

2. Нахождение рекуррентных зависимостей позволяет часто оптимизировать алгоритм, как по быстродействию, так и по объему требуемой памяти.

3. Известным примером рекуррентной последовательности второго порядка является последовательность чисел Фибоначчи:

u₁ = u₂ = 1

u_n = u_n-1+ u_n-2 , для n > 2, k=2.

4. Общая схема организации вычислений рекуррентных последовательностей:

1. Сдвиг буфера t влево.

2. Вычисление нового элемента t_k+1.

3. Запись его по индексу k+1.

4. Вычисления с t_k+1 и переход к п.1.

3.1. Примеры рекуррентных вычислений

Пример 1. Вычислить n-ое число Фибоначчи.

k=2, поэтому буфер состоит из 3-х переменных t1, t2, t3.

Function Fib (n:Integer):Integer;

Var t1, t2, t3, i :Integer;

Begin

t2:=1; t3:=1; { начальная установка буфера}

For i:=3 To n Do Begin

t1:=t2; t2:=t3; { сдвиг буфера}

t3:=t1 + t2; { вычисление нового элемента}

End;

Fib := t3;

End;

Пример 2. Вычислить значение многочлена при заданном х.

c₀x^m + c₁x^m-1 +… + c_m

Сразу рекуррентные зависимости здесь не видны, однако, если воспользоваться схемой Горнера, то получим:

(…((c₀x + c₁)x + c₂)x + … )x + c_m

Алгоритм:

Var c: Array [0..m] Of Real; { массив коэффициентов с }

sp, st : Real; { буфер}

…………………………………………………………

1-ый вариант:

st := c[0];

For i:= 1 To m Do Begin

sp := st; { сдвиг буфера}

st := sp*x + c[i]; { вычисление нового элемента}

end;

2-ой вариант: - можно обойтись одной переменной s.

s := 0;

For i:= 0 To m Do s := s*x + c[i]; {результат накапливается в s}

автоматически формирует S_нач

3.2. Двумерные рекуррентные вычисления.

Рассмотрим применение 2-мерных рекуррентных вычислений.

C 0 1 2 3 4 5 6 7
0	1
1	1	1
2	1	2	1
3	1	3	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1
6	1	6	15	20	15	6	1
7	1	7	21	35	35	21	7	1

что ( i, j ) - элемент треугольника Паскаля есть число сочетаний из i по j:

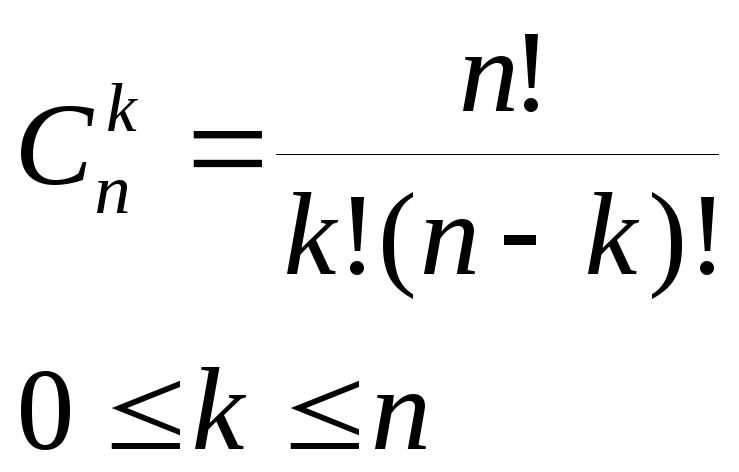- определяет сколько можно образовать подмножеств из k

элементов, если задано множество из n элементов

Пример 1.. Требуется напечатать первые строки треугольника Паскаля [6] с нулевой по n. Если через c ( i, j ) обозначить число, стоящее в i-й строке на j-м месте, то по определению треугольника Паскаля справедливы соотношения:

c _{i ,0} = c _{i, i} = 1;

c _{i, j} = c _{i -1, j-1} + c _{i -1, j}, i ≥ 0, 0 < j < i

1 вариант. Если буквально воспользоваться определением треугольника Паскаля, получается следующая процедура:

Var С :Array [0. .n-1, 0. .n-1] Of Integer;

……………………………………………………………..

For i:=0 To n-1 Do Begin

C[ 1, i ] := 1; C[ i, i ] := 1;

For j:=1 To i -1 Do

C [ i, j ] := C [ i -1, j -1 ] + C [ i -1, j ];

End;

Вывод матрицы С.

2 вариант. Подумаем, как уменьшить объем необходимой памяти. При вычислении очередной строки используются не все ранее найденные элементы треугольника, а только предыдущая строка. Печатать строки треугольника можно не в конце программы, а по мере их вычисления. Значит, достаточно двух одномерных массивов, в которых по аналогии с рекуррентной последовательностью первого порядка будут вычисляться строки треугольника. Чтобы избежать лишних копирований массивов, заведем указатели на массивы p и t, значения которых будем попеременно обменивать.

Type tm = Array[ 0. .n -1] Of Integer;

Var p, t :^tm;

Begin

New ( p ); New ( t );

p^[0] := 1; {первый элемент в всегда в 1}

For i := 0 To n -1 Do Begin

t^[i]:=1; {диагональный элемент всегда в 1}

For j := 1 To i -1 Do

t^[j] := p^[ j -1] + p^[ j ];

Вывод t^;

Обмен p и t;

End;

Dispose(p); Dispose(t);

End.

Процедура усложнилась, но и экономия памяти по сравнению с предыдущим вариантом существенная: в массивах хранится 2n чисел вместо n×n.

3 вариант. Можно, однако, уменьшить расход памяти еще в два раза, если обойтись одним одномерным массивом и вычислять очередную строку треугольника Паскаля на месте предыдущей. Элементы строки целесообразно вычислять справа налево, чтобы изменять значения только тех компонент массива, которые в дальнейшем не понадобятся.

Var t :tm;

…………………………………………………………………..

For i := 0 To n – 1 Do Begin

t [ i ] := 1; { при i = 0 → t [ 0 ] = 1 }

For j := i - 1 DownTo 1 Do t [ j ] := t [ j – 1 ] + t [ i ];

Вывод t;

End;

По сравнению с первоначальным вариантом мы не только сократили расход памяти , но и получили более изящную процедуру.

Конечно, наибольший эффект получается тогда, когда удается по-новому посмотреть на поставленную задачу. Но и следование несложному правилу — потреблять информацию сразу после ее получения — способно существенно снизить расход памяти.

Матрица А
i/j	1	2	3	4	5	6
1	1	1	1	1	1	1
2	0	1	1	1	0	1
3	1	1	1	1	1	1
4	1	1	0	1	1	1
5	1	0	1	1	0	1

Пример 2. В матрице А c n строками и m столбцами, состоящей из 0 и 1, необходимо найти квадратный блок максимального размера, состоящий из одних единиц. Под блоком понимается множество элементов соседних (подряд идущих) строк и столбцов матрицы. Интересующая нас часть показана на рисунке.

Таблица значений T(i,j) Матрица В
i/j	1	2	3	4	5	6
1	1	1	1	1	1	1
2	0	1	2	2	0	1
3	1	1	2	3	1	1
4	1	2	0	1	2	2
5	1	0	1	1	0	1

Положение любого квадратного блока может быть опреде­лено его размером и положением одного из его углов. Пусть T(i, j) есть функция, значение которой соответст­вует размеру максимального квадратного блока, состоящего из одних единиц, правый нижний угол которого расположен в позиции (i, j). Функция T(i, j) вычисляет элемент матрицы B[i, j]. На следующем рисунке показаны значения T(i, j).

Таким образом, наша задача свелась к вычислению максимального значения функ­ции Т при всевозможных значениях параметров i и j. Этой функции может быть поставлена в соответствие таблица размера n·m.

Определим сначала значения элементов матрицы В, расположенных в первой строке и в первом столбце. Получим:

В[1, 1] = А[1, 1],

В[1, j] = А[1, j] при j≥2,

В[i, 1] = A[i, 1] при i≥2.

Эти соотношения следуют из того факта, что в этих случаях рассматриваемая об­ласть матрицы А содержит только один элемент матрицы.

При 2 ≤ i ≤ n и 2 ≤ j ≤ m для этой функции можно записать следующие рекуррентные соотношения:

B[i, j] = 0, если A[i, j] = 0 и

B[i, j] = Min ( B[i - 1, j], B[i, j - 1], B[i - 1, j - 1]) + 1, если A[i, j] = 1.

Первое соотношение показывает, что размер максимального единичного блока с правым нижним углом в позиции (i, j) равен нулю в случае A[i, j] = 0. Убедимся в правильности второго соотношения. Действительно, величина B[i - 1, j] соответствует максимальному размеру единичного блока таблицы A с правым нижним углом в позиции (i - 1, j). Тогда размер единичного блока с правым ниж­ним углом в позиции (i, j) не превышает величину B[i - 1, j] + 1, так как к блоку в позиции (i - 1, j) могла добавиться только одна строка. Величина B[i, j - 1] соответ­ствует максимальному размеру единичного блока таблицы A с правым нижним уг­лом в позиции (i, j - 1). Тогда размер единичного блока с правым нижним углом в позиции (i, j) не превышает величину B[i, j - 1] + 1, так как к блоку в позиции (i - 1, j) мог добавиться только один столбец. Величина B[i - 1, j - 1] соответствует мак­симальному размеру единичного блока таблицы A с правым нижним углом в пози­ции (i - 1, j - 1). Тогда размер единичного блока с правым нижним углом в позиции (i, j) не превышает величину B[i - 1, j - 1] + 1, так как к блоку в позиции (i - 1, j - 1) могли добавиться только одна строка и один столбец. Итак, размер единичного блока с правым нижним углом в позиции (i, j) равен Min(B[i - 1, j], B[i, j - 1], B[i - 1, j - 1]) + 1.

…………………………………

В[1, 1]: = A[1, 1];

For j:=2 To 6 Do В[1, j]: = A[1, j];

For i:= 2 To 5 Do В[i, 1]: = A[i, 1];

For i:=2 To 5 Do

For j:=2 To 6 Do

If A[i, j]: = 1

Then B[i, j]: = Min(B[i - 1, j - 1], B[i, j - 1], B[i - 1, j]) + 1;

Else B[i, j]: = 0;

…………………………………..

Замечание. Рассмотренные варианты вычисления треугольника Паскаля носят скорее учебный характер. Но и на практике рекуррентные схемы вычислений и организации данных находят широкое применение – особенно в области обработки изображений. Например [10], известная операция выделения на изображении «скелета» может быть сведена к рекуррентным вычислениям, подобным рассмотренными в варианте 2, однако различие состоит в том, что значение t^[ j ] есть функция не только от p^[j-1] и p^[j], но и от t^[ j-1 ]:

t^[ j ] = F( p^[j-1], p^[j], t^[ j-1 ] ).

В данном случае возможна следующая модификация рассмотренной схемы вычислений. Пусть вместо динамических используются статические массивы. Чтобы избавиться от второго буферного массива p вводятся две дополнительные одиночные переменные a и b. Все вычисления в данный момент времени производятся в окне вычислений. Обозначим как с и d элементы окна - t]j-1] и t[j] соответственно. На самом деле, если бы использовались два буфера они в данный момент времени хранили бы информацию соответствующую p[j-1] и p[j]. Перемещая информацию надлежащим образом в окне вычислений удается и здесь сократить объем необходимой памяти. Схема вычислений приведена ниже:

For i := 0 To n -1 Do Begin {перебор строк изображения}

a := 0;

For j := 1 To n - 1 Do Begin {просмотр буфера t}

b := a; { b := t[j-1] }

a := F( с, d, b ); { вычисление нового значения }

c :=b;

End;

Вывод t;

Еnd;