
- •Комплексные числа и элементарные функции комплексного переменного
- •Комплексные числа
- •1. Понятие комплексного числа. Алгебраическая форма комплексного числа.
- •2. Тригонометрическая и показательная формы комплексного числа.
- •Произведение комплексных чисел в тригонометрической и показательной формах
- •Частное комплексных чисел в тригонометрической и показательной формах
- •Извлечение корня целой положительной степени из комплексного числа
- •Элементарные функции комплексного переменного.
- •1. Показательная функция комплексного переменного.
- •2. Логарифмическая функция комплексного переменного.
- •3. Тригонометрические функции комплексного переменного.
- •4. Обратные тригонометрические функции комплексного переменного.
- •5. Гиперболические функции комплексного переменного.
- •6. Обратные гиперболические функции.
- •Задачи для самостоятельной работы
- •Комплексные числа и элементарные функции комнлексного переменного
Частное комплексных чисел в тригонометрической и показательной формах
Для комплексных
чисел
и
частное
может быть записано в следующем виде
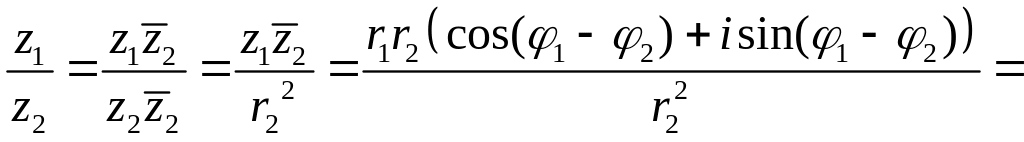
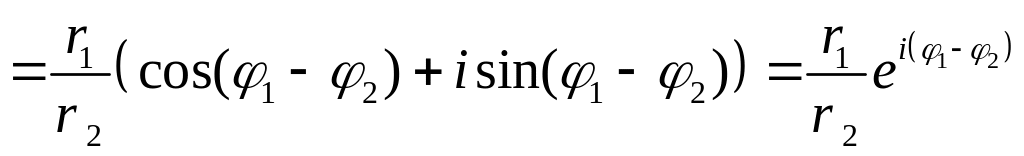 ,
откуда следует, что модуль
частного двух комплексных чисел равен
отношению модулей делимого и делителя,
а главное значение
аргумента
частного с точностью до
равно разности
аргументов делимого и делителя.
,
откуда следует, что модуль
частного двух комплексных чисел равен
отношению модулей делимого и делителя,
а главное значение
аргумента
частного с точностью до
равно разности
аргументов делимого и делителя.
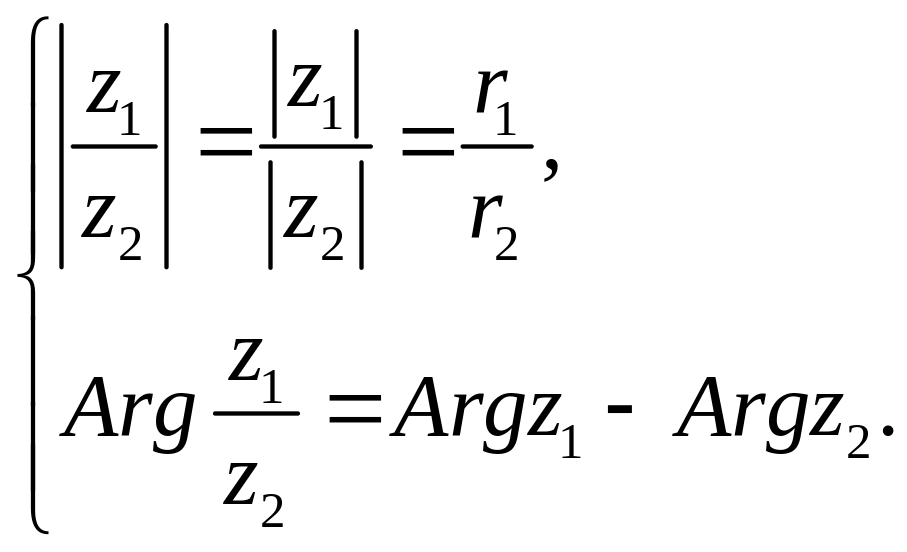 (9)
(9)
Пример 18. Представить в показательной форме числа
а)
![]() ; б)
; б)
![]() .
.
Решение. а)
![]() .
Для этого числа
.
.
Для этого числа
.
![]() ,
поэтому
,
поэтому
![]() .
.
б)
Найдем модуль
и аргумент числа
,
предварительно представив его в
алгебраической форме.
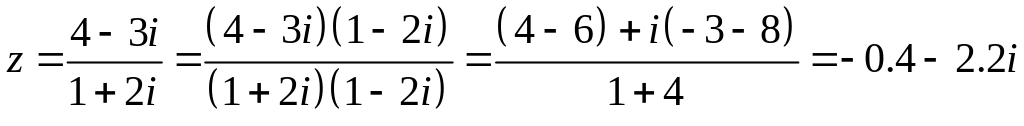 .
.
![]() - алгебраическая форма данного числа и
- алгебраическая форма данного числа и
![]() ,
,
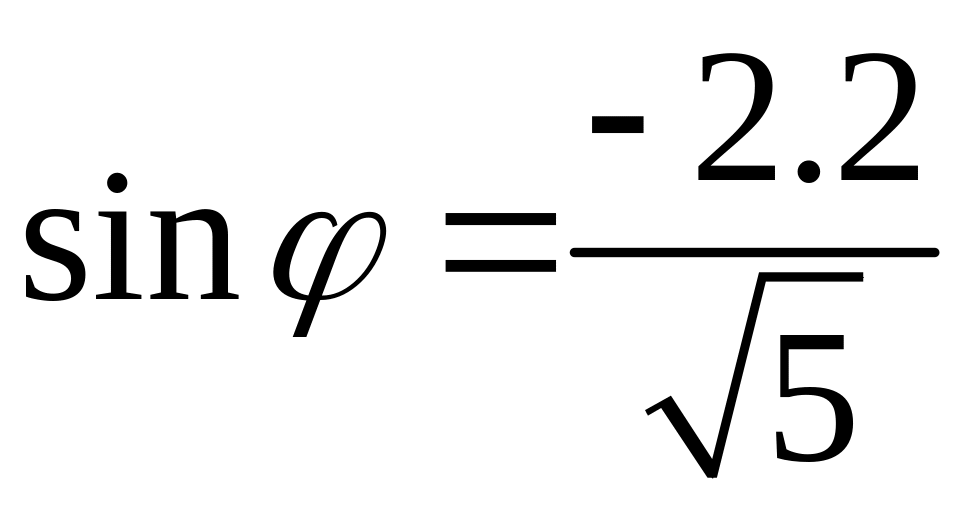 ,
,
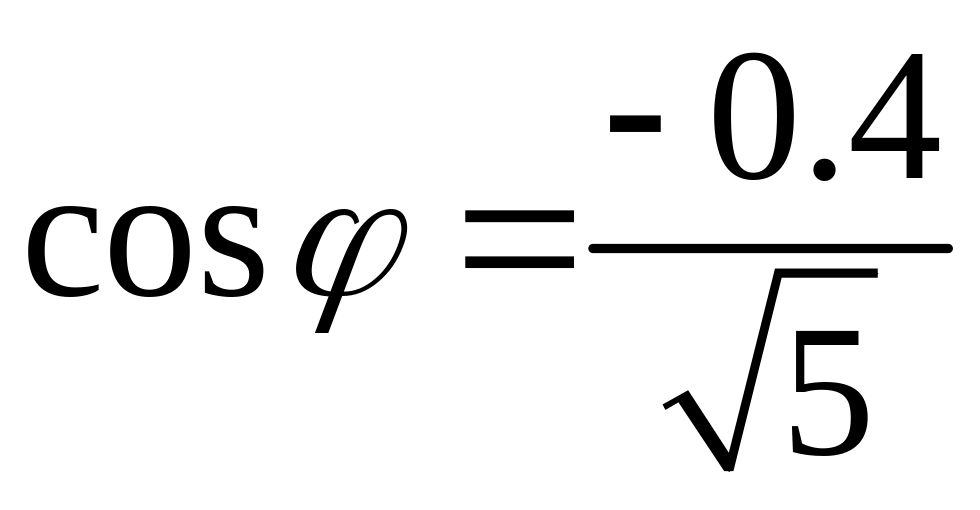 .
.
Так как действительная
и мнимая части числа
отрицательны, то главное значение
аргумента равно
![]() ,
т.е.
,
т.е.
![]() и
и
![]() .
.
Замечание. При сложении и вычитании комплексных чисел, как правило, целесообразнее использовать алгебраическую форму этих чисел. При умножении, возведении в степень и извлечении корня более рациональным может оказаться тригонометрическая или показательная форма.
Извлечение корня целой положительной степени из комплексного числа
Извлечь корень
целой положительной степени
![]() из числа
значит найти такое число
из числа
значит найти такое число
![]() ,
,
![]() -ая
степень которого равна
.
-ая
степень которого равна
.
Пусть
![]() .
Тогда
.
Тогда
![]() и
и
![]() ,
откуда
,
откуда
![]() ,
,
![]() и
и
![]()
![]() ,
откуда
,
откуда
![]() ,
(10)
,
(10)
т. е.
![]() ,
,
![]() .
.
(10) - формула для извлечения корня целой положительной степени из комплексного числа .
Пример 19
Представить следующие выражения в
алгебраической форме: а)
![]() ;
б)
;
б)
![]() .
.
Решение.
а)
![]() ,
,
![]() ,
откуда
,
откуда
![]() и
и
![]() .
.
б)
![]()
При
![]()
![]() и
и
при
![]()
![]() .●
.●
Пример 20.
Решить уравнение
![]() и изобразить корни этого уравнения на
комплексной плоскости.
и изобразить корни этого уравнения на
комплексной плоскости.
Решение.
![]()
![]()
![]()
Подставляя
последовательно
![]() ,
,
![]() ,
и
,
и
![]() ,
получим четыре
различных корня исходного уравнения:
,
получим четыре
различных корня исходного уравнения:
![]() ,
,
![]() ,
,
![]()
 и
и
![]()
(рис. 15).●
Рис. 15
ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОго ПЕРЕМЕННОго.
Понятие функции комплексного переменного вводится по аналогии с понятием функции действительной переменной.
Определение.
Величина
![]() называется функцией
комплексного переменного
в области
называется функцией
комплексного переменного
в области
![]() ,
если задан закон, по которому каждому
значению
,
если задан закон, по которому каждому
значению
![]() ,
ставится в соответствие одно или
несколько значений
.
,
ставится в соответствие одно или
несколько значений
.
Это соответствие
обозначается в виде
![]() .
.
Определение. Переменную называют независимой переменной или аргументом, а - зависимой переменной или функцией.
Пусть
![]() .
Тогда
из
имеем
.
Тогда
из
имеем
![]() и
и
![]() .
.
Определение. Если каждому значению поставлено в соответствие одно и только одно значение , то функцию называют однозначной, а если несколько значений – то многозначной.
Определение.
Множество значений
![]() ,
где
,
называется областью
значений функции
и обозначается это множество через
,
где
,
называется областью
значений функции
и обозначается это множество через
![]() .
.
Геометрически
можно рассматривать
,
заданную на
,
как отображение области
плоскости
(рис. 16) в некоторую область
плоскости
![]() .
.
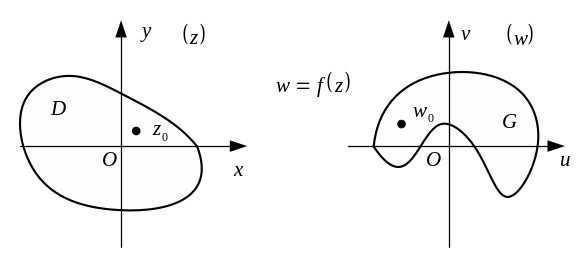
Рис. 16
Определение.
Если
![]() ,
то точка
,
то точка
![]() называется образом
точки
при отображении
,
а точка
называется
прообразом
точки
.
называется образом
точки
при отображении
,
а точка
называется
прообразом
точки
.
З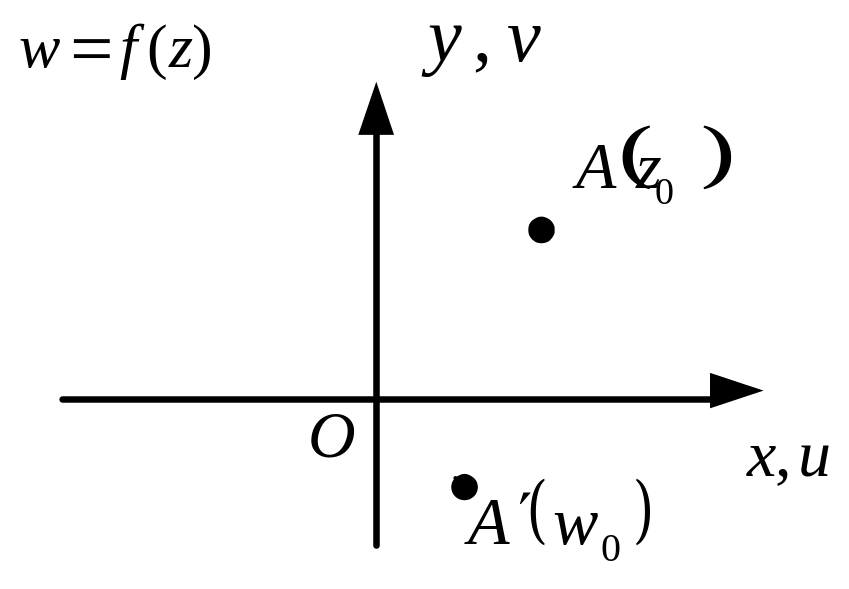 амечание.
Иногда удобно совмещать плоскости
и
.
Тогда функция
«перемещает» точку
амечание.
Иногда удобно совмещать плоскости
и
.
Тогда функция
«перемещает» точку
![]() в точку
в точку
![]() (рис. 17).
(рис. 17).
Рис.
17
Например,
при отображении
![]() образом точки
образом точки
![]() является точка
является точка
 ,
т. е
,
т. е
функция
«перемещает» точку
![]() в точку
в точку
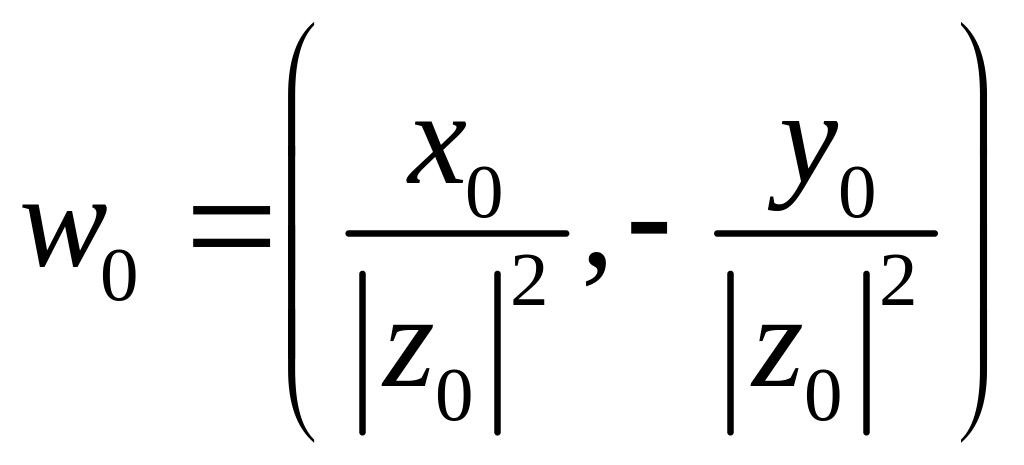 .
Очевидно,
.
Очевидно,
![]() .
.
Пример 21
Найти образ точки
![]() ,
если отображение задано формулой
,
если отображение задано формулой
![]() .
.
Решение.
![]() .●
.●
Пример 22.
Найти уравнения линий в плоскости
![]() ,
на которые с помощью функции
,
на которые с помощью функции
![]() отображаются прямые
и
отображаются прямые
и
![]() .
.
Решение.
![]() ,
,![]() ,
откуда
,
откуда
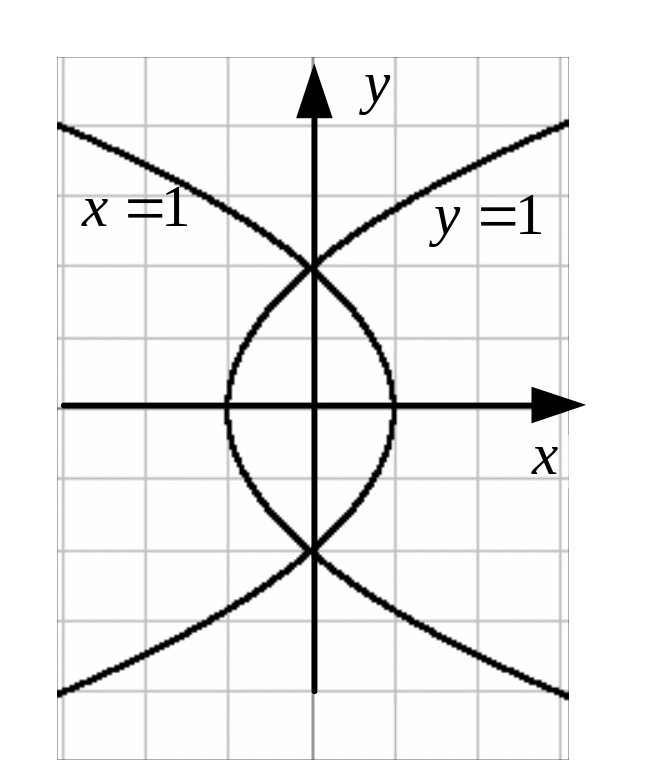
![]() ,
,![]() . (11)
Подставляя
в уравнения (11), получим
. (11)
Подставляя
в уравнения (11), получим
![]() ,
,![]() ,
откуда
,
откуда
![]() .
Это , уравнение
.
Это , уравнение
параболы, симметричной
относительно оси
![]() .
.
Подставляя
в уравнения (11), получим
![]() ,
,
![]() ,
т.е. еще одну параболу
,
т.е. еще одну параболу
![]() (рис. 18).●
(рис. 18).●
Рис. 18 Пример 23. Найти образ окружности при отображении .
Решение 1.
Так как
,
то
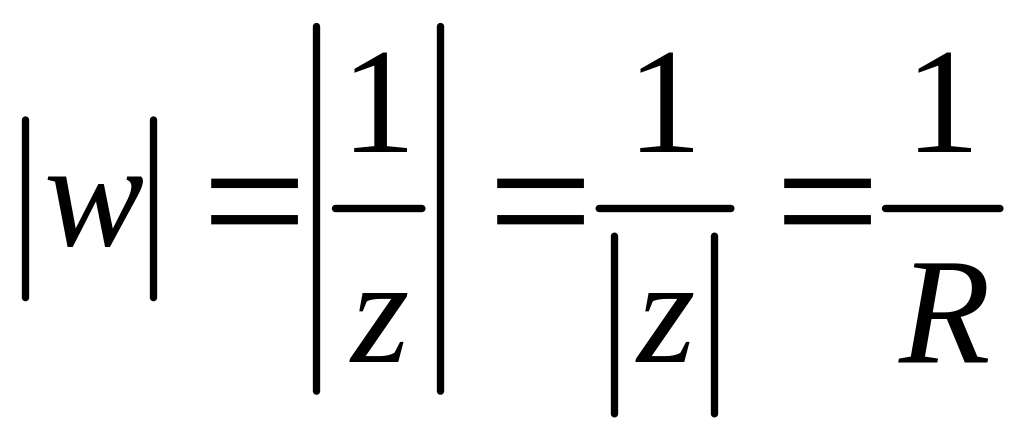 ,
т. е. образом окружности
при указанном отображении является
окружность
,
т. е. образом окружности
при указанном отображении является
окружность
![]() .
.
Решение
2.
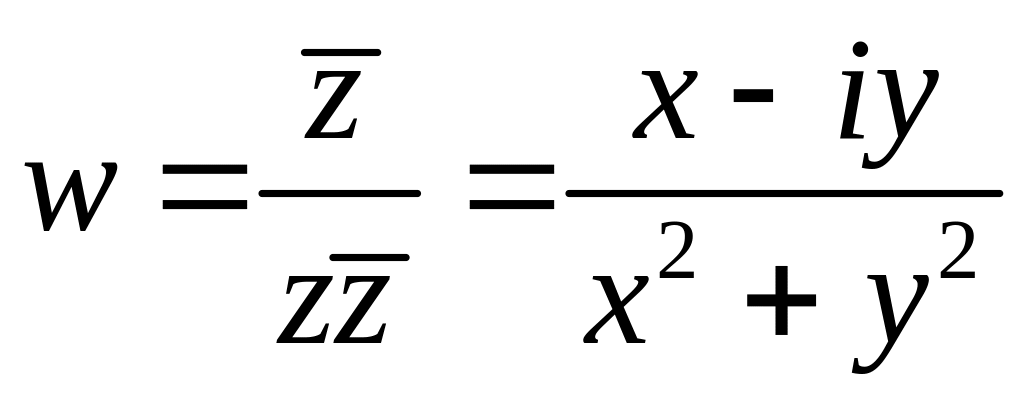 ,
откуда
,
откуда
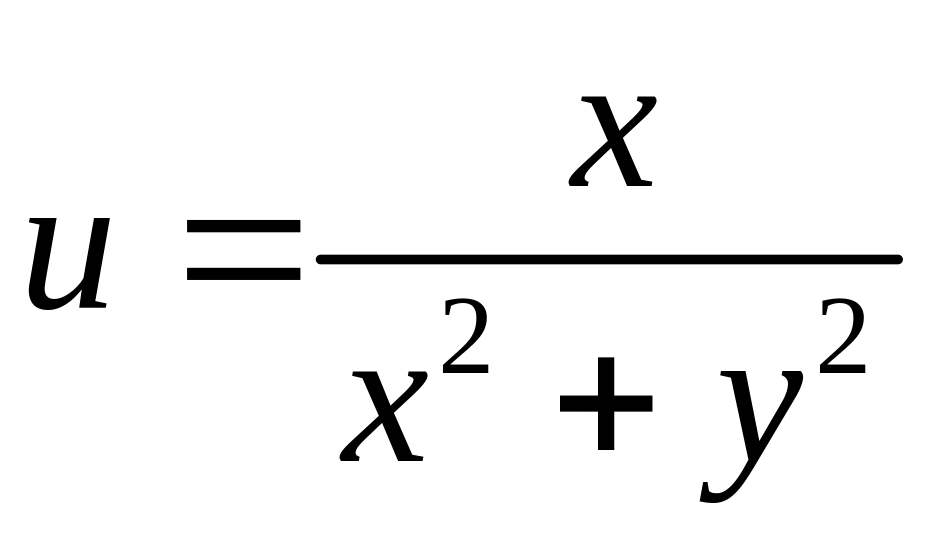
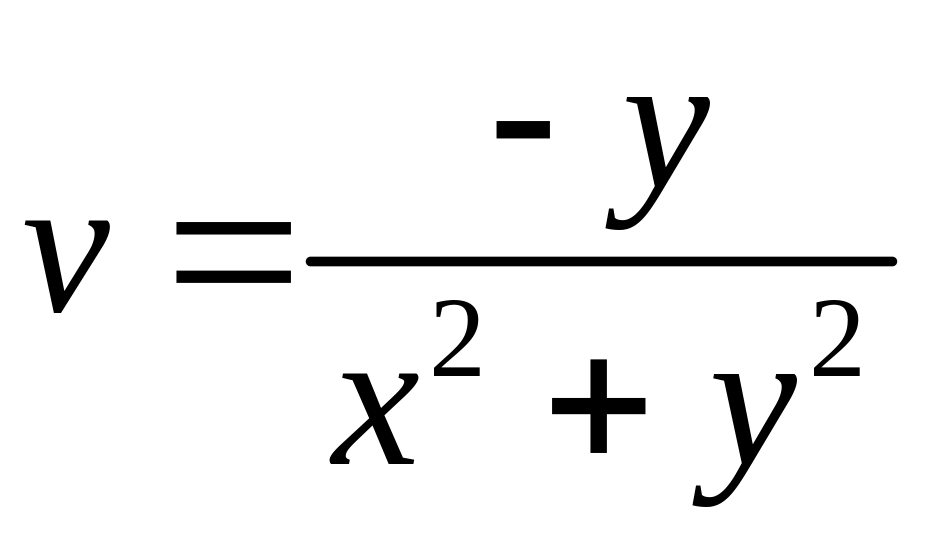 .
.
Так как
,
то
,
![]() ,
,
![]() и
и
![]() ,
т.е. образом окружности
при отображении
является окружность
.●
,
т.е. образом окружности
при отображении
является окружность
.●
