
Supersymmetry. Theory, Experiment, and Cosmology
.pdf
Supersymmetry breaking 129
it is also this nonvanishing vacuum value which generates a field independent term in the Goldstino supersymmetry transformation.
It is customary to introduce a supersymmetry breaking scale MSB and write on |
|||||||
dimensional grounds F |
i |
¯¯ |
4 |
|
|
|
|
|
gi¯F ≡ MSB . Then, |
|
|||||
|
|
|
m3/2 = |
MSB2 |
(6.50) |
||
|
|
|
mP √ |
|
. |
||
|
|
|
3 |
||||
6.3.2Hidden sector
When discussing the issue of supersymmetry breaking in Chapter 3, we have encountered di culties when there is a direct coupling between the supersymmetrybreaking fields and the quark and lepton fields. In the case of F -term breaking (O’Raifeartaigh model of Section 3.1.4), the spectrum obtained is unrealistic (STr M 2 = 0). In the case of D-term breaking (see Section 3.2.2), one faces quantum anomalies.
The idea is therefore to somewhat decouple the sector of supersymmetry breaking from the observable sector of quarks, leptons and gauge interactions. One refers to the former as a hidden sector. Obviously, one cannot totally “hide” this sector since the information of supersymmetry breaking must reach the observable sector. But, in the context of supergravity, gravity itself provides a necessary coupling between the two sectors. As we will see, the gravitational coupling between the two sectors tends to soften the divergences: whereas supersymmetry breaking e ects are of orderF MSB2 m3/2 mP l in the hidden sector, they are damped by the gravitational coupling κ m−P l1 in the observable sector and one expects there e ects of order m3/2 . We will see below that indeed soft supersymmetry breaking terms are of the order of the gravitino mass (or smaller if more powers of κ are involved). This means that, barring accidental cancellations, one expects STr M 2 ≡ TrM02 − 2TrM12/2 to be of
order m2 . For example, for a single (gauge singlet) chiral superfield z coupled to
3/2
supergravity, the supertrace, including terms up to spin 3/2, reads [209]
|
|
3/2 |
|
|
|
|
Gz Gz¯ |
|
Rzz¯ |
|
|
|
||
S |
TrM 2 |
≡ J=0 |
( |
− |
)2J (2J + 1) TrM 2 |
= 2eG |
|
|
, |
(6.51) |
||||
|
|
|
||||||||||||
|
|
J |
|
G |
zz¯ |
|
G |
zz¯ |
min |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
where Rzz¯ is the curvature of the K¨ahler manifold: Rzz¯ = −∂z ∂z¯ ln |
Gzz¯ [see (C.57) of |
|||||||||||||
Appendix C]. Then, for a flat K¨ahler manifold (Gzz¯ = 1 hence Rzz¯ = 0), we have, for
√
z = (A + iB)/ 2 (the corresponding fermion field is the Goldstino; it disappears from the physical spectrum):
m2 |
+ m2 |
= 4m2 . |
(6.52) |
A |
B |
3/2 |
|
We have seen in Chapter 3, after equation (3.23) that STr M 2 measures approximately the di erence between an average supersymmetric particle mass and an average quark/ lepton mass. As such, it should be of the order of the (TeV)2. This explains why a gravitino mass of a few hundred GeV or a TeV is often quoted as a preferred value (although there exists viable models with a superlight or superheavy gravitino).
We now illustrate these ideas on a very simple model, known as the Polonyi [313] model, which has provided for a long time a guideline for this type of gravity-mediated supersymmetry breaking.

130 Supergravity
The hidden sector consists of a single chiral supermultiplet with scalar component denoted by z and a superpotential
Wh(z) = µmP (z + β). |
(6.53) |
Since Fz = dWh/dz = µmP = 0, supersymmetry is broken (and arguments above suggest to take µ in the 100 GeV to 1 TeV range); β is a real constant of order mP to be fixed below. One then adds observable supermultiplets, with scalar field components denoted by φi. If we assume that the complete potential has the form
W(z, φi) = Wh(z) + Wo(φi), |
(6.54) |
then the scalar potential reads in the limit of global supersymmetry (i.e. for vanishing gravitational coupling: κ → 0)
|
|
|
|
2 |
|
|
|
2 |
|
|
V(z, φi) = |
|
dW |
|
+ |
i |
|
∂W |
. |
(6.55) |
|
dzh |
∂φio |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hence, the two sectors are completely decoupled. If we restore a nonvanishing κ, we see that the two sectors are coupled only gravitationally.
In order to discuss such couplings, we must specify the K¨ahler potential; for simplicity, we will choose a flat K¨ahler metric:
|
|
|
|
|
|
|
|
i |
¯¯ı |
i ¯¯ı |
|
|
|
|
|
|
|
|
|
|
K(z, z,¯ φ |
, φ ) = zz¯ + φ |
φ . |
|
|
|
|||
The scalar potential (6.36) then reads |
|
|
|
|
|
|
||||||||
2 |
2 |
i ¯¯ı |
|
|
dW |
|
|
|
2 |
|
∂W |
|
||
|
|
|
|
|
||||||||||
|
|
|
|
|
+ |
|
+ κ2φ¯¯ı(Wh |
|||||||
V(z, φi) = eκ |
(|z| |
+φ φ ) |
dzh + κ2z (Wh + Wo) |
∂φio |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3κ |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|Wh + Wo| |
. |
|
|
|
|
|
|||||
(6.56)
2
+ Wo)
(6.57)
Since only z acquires a vacuum expectation value of order mP l , it is consistent to consider first this field alone by setting the φi to zero. Requiring a vanishing cosmological constant at the minimum z of V(z, 0) tunes the constant β:
√
κβ = ±2 − |
3 |
||
√ |
|
|
|
κ z = 3 1
and the gravitino mass reads from (6.46):
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
m3/2 |
= µe2 |
3 |
. |
|
|
|
|
|
|||
We note that |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
dW |
|
|
|
2 |
2 |
|
√ |
|
|
|||
|
|
|
|
|
|
|||||||||||
.eκ |
|z| |
/2 |
|
h |
+ κ2z Wh |
/ |
= κ√3 Wheκ |
|z| |
/2 = |
3 |
m3/2 . |
|||||
|
dz |
κ |
||||||||||||||
(6.58)
(6.59)
(6.60)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Supersymmetry breaking |
131 |
|||
Hence, we can write |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V( z , φi) = eκ2|φi|2/2 √ |
|
|
κ−1m3/2 + κ(√ |
|
1)W |
2 |
|
||||||||||||||||||||
3 |
3 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
∂W |
|
|
|
|
2 ¯¯ı |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯¯ı |
|
|
||||||||
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
i |
|
∂φi |
+ κ φ W + m3/2 φ |
|
|
|
|||||||||||||||||||
|
− |
3 |
|
κ− |
|
m3/2 + κW |
% |
|
|
|
|
|
(6.61) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
where |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
W (φi) ≡ eκ2| z |2/2Wo(φi). |
|
|
(6.62) |
|||||||||||||||||||||||
In the limit κ → 0, finite m3/2 |
and finite κ z , we have |
|
|
|
|||||||||||||||||||||||
i |
|
∂W |
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V( z , φ ) |
i |
|
|
|
∂φi |
|
|
+ m3/2 |
|
|
i |
φ |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
i ∂W |
|
+ (A − 3)W + h.c. , |
|
|||||||||||||
|
+m3/2 |
i |
φ |
|
|
|
|
|
(6.63) |
||||||||||||||||||
|
|
|
∂φi |
||||||||||||||||||||||||
with |
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.64) |
|||
|
|
|
|
|
|
A = 3 |
|
3 |
. |
|
|
|
|
|
|
||||||||||||
We recognize:
•in the first term the standard scalar potential of global supersymmetry;
•in the second term, scalar masses of order m3/2 ;
•in the third term, analytic terms in φi plus their hermitian conjugates. The con-
stant A has been introduced because for a cubic potential W (φ) = λφ3, these
terms simply read Am3/2 λ φ3 + φ 3 . This is a standard A-term of the type discussed in Section 5.2.3 of Chapter 5.
We see that we have generated through gravitational interactions soft supersymmetrybreaking terms in the observable sector precisely of the order of the gravitino mass m3/2 : scalar masses6 and A-terms. One may wonder about the last type of soft terms, gaugino masses. It turns out that the full supergravity Lagrangian includes a term:
L|quad λ = Re f (z, φi) |
i |
|
|
1 |
∂f |
|
|
|
|||
|
|
λγ¯ |
µ∂µλ − |
|
|
|
Fz λ¯R |
λL |
+ h.c. |
(6.65) |
|
4 |
4 |
∂z |
|||||||||
where the gauge kinetic function f (z, φi) is defined in (6.25). Using (6.32), we findFz of order m3/2 κ−1. Thus, we obtain gaugino masses of order m3/2 as well if the gauge kinetic function depends on z.
6The other type of analytic mass term in equation (5.6) of Chapter 5 may be recovered from the last line in (6.63) if W (φ) includes a quadratic term ρφ2: then δm 2 = (A − 1)ρm3/2 .
132 Supergravity
6.4The gravitino and Goldstino fields
It is time to pause and to discuss in some more detail the physics associated with this spin 3/2 field which provides the supersymmetric partner of the graviton: the gravitino.
We first consider the massless gravitino described by the Majorana spin-vector ψrµ (r spinor index and µ vector index). The free field equation of motion simply reads in flat space:
λµνργ5γµ∂ν ψρ = 0, |
(6.66) |
which is invariant under the gauge transformation ψµ → ψµ + ∂µη, with η a Majorana spinor. Equation (6.66) is known as the Rarita–Schwinger [321] equation.
It can also be written, using (B.21) of Appendix B:
iγ[µγν γρ]∂ν ψρ = 0, |
(6.67) |
which has the advantage of being suitable for generalization to higher dimensions (see Chapter 10).
We make the standard gauge choice of the harmonic gauge:
|
γρψρ = 0. |
|
ψ |
|
+ ∂ |
|
η with γρ∂ |
|
(6.68) |
||||
This leaves us with a residual gauge |
symmetry ψ |
µ →µ |
µ |
µ |
ρ |
η = 0. |
|||||||
|
ν |
|
µ |
|
ν |
|
|
|
|||||
With this gauge choice, (6.67) reads γ |
|
∂ν ψ |
|
− γ |
∂ν ψ |
= 0. Contracting with γµ |
|||||||
gives |
∂ν ψν = 0 |
|
|
|
|
|
|
|
|
(6.69) |
|||
|
|
|
|
|
|
|
|
|
|||||
and thus |
γρ∂ρψµ = 0 |
|
|
|
|
|
|
|
|
(6.70) |
|||
|
|
|
|
|
|
|
|
|
|||||
which is the Dirac equation for a massless fermion field.
The spin-vector ψrµ belongs a priori to the representation (1/2) (1) = (1/2) (3/2). The condition γρψρ = 0 above selects the (3/2) representation: it is an irreducibility condition. To see this, we decompose ψµ in momentum (p) space using the complete set provided by the vector (e.g. photon) polarization states7 ε±µ associated with helicity ±1, the momentum pµ and a conjugate momentum p¯µ such that p¯2 = p2 = 0 and pµp¯µ = 1:
ψrµ = εµ+ur+ + εµ−ur− + pµur + p¯µvr, |
(6.71) |
where u±, u and v are spinor fields. From (6.69), we have pρψρ = 0 and thus v = 0, whereas (6.70) yields γρ∂ρu± = γρ∂ρu = 0. We then use the residual gauge symmetry (see the comment following equation (6.68)) to absorb the term pµur:
ψrµ = εµ+ur+ + εµ−ur−. |
|
|
(6.72) |
Then the irreducibility condition (6.68) yields: |
|
|
|
0 = γρερ−γσψσ = γρερ−γσ εσ+u+ = 1 − |
piΣi |
|
|
|
u+, |
(6.73) |
|
|p| |
|||
7They satisfy ε±µ pµ = 0 (transverse polarization) and ε+µ εµ+ = 0 = ε−µ εµ− .
|
The gravitino and Goldstino fields 133 |
|||
where Σi |
is the spin matrix which takes the form |
σi |
0 |
in the basis described |
0 |
σi |
|||
in footnote 11 of Chapter 5. Hence u+ has helicity +1/2 and ε+µ u+ represents the component of helicity +3/2; similarly ε−µ u− is the component of helicity −3/2.
Let us recapitulate the counting of the number of on-shell degrees of freedom for a massless gravitino: it has the degrees of freedom of a massless vector field (2) times those of a Majorana spinor (2) but the gauge condition γρψρ = 0 kills those of the spin 1/2 part (2); we are left with 2 × 2 − 2 = 2 degrees of freedom.
This should be put in parallel with the counting of on-shell degrees of freedom of a graviton. The graviton field is obtained as a fluctuation of the metric gµν =
ηµν + hµν and is thus described by the symmetric traceless tensor hµν which has |
|||
(4 × 5)/2 − 1 (for the trace), that is nine independent components. The |
gauge freedom |
||
|
µ |
hµν ; but |
|
δhµν = ∂µξν + ∂ν ξµ is partly fixed by four gauge conditions which specify ∂ |
|
||
there is, as usual, a residual gauge invariance corresponding to ξµ satisfying ∂µξµ = 0 and ξµ = 0, which eliminates another three degrees of freedom (four massless scalars minus one condition). We are left with two on-shell degrees of freedom for the graviton.
It is thus perfectly consistent to have a gravity supermultiplet with only the graviton and the gravitino. As we have seen in Chapter 3 for other supermultiplets, the counting of o -shell degrees of freedom, on the other hand, imposes the presence of auxiliary fields, as described at the end of Section 6.1.
We now turn to the massive gravitino case. The equation of motion reads:
− |
i |
µνρσ γ5γν ∂ρψσ − m3/2 σµρψρ = 0. |
(6.74) |
|
|||
2 |
|||
Contracting with ∂µ yields, in the case of nonvanishing gravitino mass, |
|
||
|
|
[γσ ∂σ , γρ] ψρ = 0. |
(6.75) |
Then, contracting (6.74) with γµ and using the equation just obtained gives, again for m3/2 = 0,
γρψρ = 0. |
(6.76) |
Thus the gauge condition of the massless case is obtained as a consequence of the equations of motion (a similar situation is found for the case of a massive vector field, see the comment following equation (A.95) of Appendix Appendix A). One obtains:
1 |
|
1 |
|
|||
∂ρψρ = |
|
{γσ ∂σ , γρ} ψρ = − |
|
[γσ ∂σ , γρ] ψρ = 0 |
(6.77) |
|
2 |
2 |
|||||
from (6.75) and (6.76). Also the equation of motion simply reads: |
|
|||||
|
|
i µνρσγ5γν ∂ρψσ = m3/2 ψµ. |
(6.78) |
|||
Contracting this with γµγλ, one finally obtains |
|
|||||
|
|
γρ∂ρ − m3/2 |
ψλ = 0 |
(6.79) |
||
which is the standard Dirac equation for a massive spinor field.
Whereas the MSSM was strictly speaking a low energy theory, the inclusion of gravity, even at the level of the nonrenormalizable theory that is supergravity, allows
134 Supergravity
us to consider supersymmetric models up to scales close to the Planck scale. The hope is that, as one renormalizes the model up to higher scales, it becomes simpler, reflecting a symmetry principle that becomes transparent at a high fundamental scale (we will study for example in later chapters grand unification theories or string theories which provide explicit examples of such paradigms). In the remaining sections, we will therefore use renormalization group techniques to bring the low energy supersymmetric models discussed in the previous chapter to higher scales, and before considering more elaborate high energy models, we will make some simplifying assumptions at a scale close to the Planck scale to introduce a toy model known as minimal supergravity which will represent our first attempt at writing a simple high energy paradigm.
6.5Radiative breaking of SU (2) × U (1)
We start by studying the breaking of the electroweak symmetry. We have seen in Chapter 5, equation (5.13) that, in the Higgs sector, the scalar potential
V = m2 |
H10 2 + m22 |
H20 2 |
+ Bµ |
H0H0 |
+ H0 H0 |
|
|||||||
1g|2 |
+|g 2 |
|
|0 |
2 |
| |
0 |
2 |
2 |
1 2 |
1 2 |
|||
+ |
|
|
|
|H1 | |
|
− |H2 | |
|
|
|
|
|
||
|
|
8 |
|
|
|
|
|
||||||
has a nontrivial minimum under the conditions
m21 + m22 > 2|Bµ|
m21m22 < |Bµ|2
which are not compatible with m21 = m22. Luckily enough, because H1 and H2 couple to di erent fields, radiative corrections give a di erent treatment to H1 and H2, even if supersymmetry breaking yields the same contribution of order m3/2. Let us see in more detail how this arises.
The main di erence between H1 and H2 is that H2 couples to the top quark. Restricting therefore our attention to the heavy quark loops, we must consider the diagrams of Fig. 6.1 which contribute to the renormalization of the soft scalar mass
mH2 2 ≡ m22 − |µ|2. |
in the |
The first three diagrams come from the term λtQ3 · H2T c where Q3 = BT |
|
which is |
|
superpotential. Each individual diagram contributes a quadratic divergence – |
|
cancelled in the sum, since supersymmetry is spontaneously broken– and a logarithmic divergence. The fourth diagram arises from an A-term proportional to the same term λtQ3 · H2T c in the superpotential: Atλtq3L · H2tR + h.c. and the last term arises
from the Higgs gauge interactions. One obtains (see Appendix E for a more complete |
|||||||||||
formula) |
2 dmH2 2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
2 |
2 |
|
2 |
2 |
|
||
8π |
|
|
= 3λt |
mH2 |
+ mT |
+ mQ + At |
|
− 3g |
M2 |
(6.80) |
|
|
dt |
||||||||||
where t = ln(µ/µ0), µ being the renormalization scale (not to be confused with the supersymmetric parameter µ!) This should be solved with the boundary condition
m2H2 (µ = mP ) = m23/2.

Radiative breaking of SU(2) × U(1) 135
|
|
|
|
tR |
|
|
|
QL |
|
|
|
|
|
|
|
|
|
|
QL |
|
|
|
|
|
|
|
H2 |
H2 |
|
|
|
|
|
|
|
λt |
λt |
|
H2 |
λt2 |
H2 |
H2 |
λt2 |
H2 |
|
tR |
|
|
|
|
|
|
|
|
QL |
|
|
|
W |
|
|
|
|
H2 |
|
H2 |
|
H2 |
|
|
H2 |
|
λt |
|
λt |
|
g |
|
g |
|
|
|
|
|
|
|
|
||
|
t |
R |
|
|
|
H2 |
|
|
|
|
|
|
|
|
|
|
|
Fig. 6.1 One-loop diagrams contributing to the renormalization of m2H2 . Q, tR solid (resp. dashed) lines are quark (resp. squark) lines, solid W or H2 lines are gaugino or Higgsino lines.
We see that the term proportional to λt tends to decrease m2H2 as µ decreases. One should remember the relation (5.27) of Chapter 5 which we rewrite
1 |
2 |
= |
mH2 |
1 − mH2 |
2 |
tan2 β |
− |µ| |
2 |
> 0. |
(6.81) |
|
2 |
MZ |
|
tan2 β |
− |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||
This gives the condition that the soft supersymmetry breaking parameters m2H1 and m2H2 must fulfill at low energy in order to have the right breaking: the smaller m2H2 is (and possibly negative), the easier it is to fulfill.
Similar equations are obtained for the evolution of m2T and m2Q
8π2 |
dm2 |
= 2λ2 |
m2 |
+ m2 |
+ m2 |
+ A2 |
|
16 |
g2 |
|
2 |
(6.82) |
|||
T |
|
|
|
|
M |
||||||||||
|
|
|
|
|
3 |
||||||||||
|
dt |
t |
H2 |
T |
Q |
t |
|
|
|
|
3 |
|
|
||
|
|
|
|
|
|
|
− 3 |
|
|
|
|
||||
|
dm2 |
|
|
|
|
|
|
|
|
|
|||||
8π2 |
Q |
= λt2 mH2 |
2 + mT2 + mQ2 + At2 |
− |
16 |
g32 M32. |
(6.83) |
||||||||
dt |
3 |
||||||||||||||
If we can neglect the e ect of the gaugino masses M2, M3, we see that, as µ decreases, all three m2H2 , m2T and m2Q decrease but m2H2 faster than the other two: hence SU (2)× U (1) is broken before there is a danger that SU (3) gets broken (through m2T < 0 or m2Q < 0). If the e ect of M3 is nonnegligible, it will tend to slow down the evolution of m2T , m2Q, which in turn enhances the e ect on m2H2 .
To get a crude estimate of the scale µEW at which the electroweak symmetry is broken, we may neglect the running of all quantities besides mH2 . The leading contribution to the renormalization of mH2 is then, from (6.80),
|
|
3λ2 |
µ |
|
|
||
δmH2 |
2 − |
t |
mQ2 |
ln |
|
. |
(6.84) |
8π2 |
mP |
||||||
136 Supergravity |
|
|
|
|
If we start with a boundary condition where mH2 |
2 (mP ) mQ2 , then the scale µEW at |
|||
which m2 |
+ δm2 |
becomes negative is then |
|
|
H2 |
H2 |
|
|
|
|
|
µEW mP e−O(1)×4π/λt2 . |
(6.85) |
|
Hence, a large Yukawa coupling induces a scale for electroweak symmetry breaking which is exponentially small compared to the Planck scale.
In principle, however, a large top mass is not compulsory: at the time when the top mass was thought to be around 40 GeV, electroweak symmetry breaking was shown to be consistent with such a mass, although this involved some fine-tuning of the gaugino mass [48, 230].
6.6Gaugino masses
In a similar way, one should let the gaugino masses evolve from a scale of order mP l where they are typically equal to m3/2 to a low energy scale. Their renormalization group evolution is particularly simple:
|
dMi |
|
= − |
αi |
|
bi Mi |
(6.86) |
||
|
dt |
2π |
|
||||||
where αi is the corresponding gauge coupling constant which evolves as: |
|
||||||||
|
dαi |
= − |
bi |
αi2 |
(6.87) |
||||
|
|
dt |
2π |
||||||
and bi is thus the beta function coe cient at one loop (see Appendix E). One obtains
d(Mi/αi) |
= 0 |
(6.88) |
|
dt |
|||
|
|
which shows that Mi/αi is not renormalized.
Thus, if we assume equality of gauge couplings at some unification scale MU
α1(MU ) = α2(MU ) = α3(MU ) |
(6.89) |
and correspondingly (confusing MU and mP for that purpose) equality of gaugino masses at this scale8
M1(MU ) = M2(MU ) = M3(MU ) = M1/2, |
(6.90) |
where M1/2 is a constant of the order of the gravitino mass, the gaugino masses and gauge couplings at low energy are related:
M1 |
= |
M2 |
= |
M3 |
. |
(6.91) |
α1 |
α2 |
|
α3 |
|
||
In other words, the gaugino mass terms M1 and M2 which appear in the chargino/neutralino mass matrices can be expressed in terms of the single gluino mass M3. We have the following relations (see last footnote)
M3 = |
α3 |
sin2 θW M2 = |
3 α3 |
cos2 θW M1. |
(6.92) |
|||
|
|
|
|
|||||
α |
5 α |
|||||||
|
|
|
|
|||||
Hence, at the electroweak scale, M3 : M2 : M1 7 : 2 : 1.
8Note that, as usual, α1 corresponds to the normalization of the U (1) hypercharge imposed by grand unification: the U (1)Y gauge coupling used traditionally in the Standard Model is g such that α ≡ g 2/(4π) = 3α1/5 (see Chapter 9, equations (9.26) and (9.30)).
Scalar masses 137
We have seen that the equation of evolutions for the scalar masses are rather more complicated. If we assume that scalar masses are smaller than gaugino masses at all scales, the gaugino loop contribution dominates in equations such as (6.82–6.83) and the renormalization group evolutions are easy to solve. One finds, to a good approximation,
M32(MZ ) 9.8 M12/2, |
|
mQ2 (MZ ) mQ2 (MU ) + 8.3 M12/2, |
|
mU,D2 (MZ ) mU,D2 (MU ) + 8 M12/2, |
(6.93) |
mL2 (MZ ) mL2 (MU ) + 0.7 M12/2, |
|
mE2 (MZ ) mE2 (MU ) + 0.23 M12/2. |
|
6.7Scalar masses
There is however a severe problem connected with scalar masses arising from supersymmetry breaking: the problem of flavor changing neutral currents (FCNC). The origin of these FCNC is similar to the Standard Model but there is, in general, no equivalent to the GIM cancellation mechanism (see Section A.3.4 of Appendix Appendix A).
Let us recall that, in general, the nondiagonal nature of Yukawa couplings leads, after gauge symmetry breaking, to nondiagonal quark and lepton mass matrices. One thus needs to diagonalize them through some matrices V q, .
Similarly, we have seen earlier that supersymmetry breaking leads to nondiagonal squark and slepton mass matrices, which may be diagonalized through some matrices
V q, .
As long as the two issues – supersymmetry breaking and Yukawa couplings – are not connected, there is no reason to relate V q, with V q, , i.e. the rotations among quarks and leptons and the rotation of squarks and sleptons. This leads to undesirable
FCNC’s. Let us consider for example the |
squark–quark–gluino coupling: q |
† |
¯ |
|
q, where |
||||||
λ |
g |
||||||||||
|
|
|
|
|
|
|
|||||
If |
|
|
|
|
|
|
|
|
|
|
|
q and q are, respectively, the quark and squark fields which are interaction eigenstates |
|||||||||||
(i.e. the original fields in the interaction Lagrangian). |
|
|
|
|
|||||||
one wants to express this coupling in terms of the mass eigenstates one needs |
|||||||||||
to make the rotations just introduced: q†V q† λ¯ |
V q q. In other words, we have a flavor |
||||||||||
mixing matrix |
|
|
q† |
|
g q |
. |
|
|
|
|
|
|
W ≡ V |
V |
|
|
|
|
|
||||
In general, W = |
1, which generates |
FCNC. Let us consider for example the fa- |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
¯ |
→ sd¯ amplitude which contributes to the KL–KS mass di erence ∆mK (see |
mous sd |
Fig. A.6 of Appendix Appendix A). As long as W = 1, there is a new contribution coming from the following box diagram involving gluinos and squarks as shown in Fig. 6.2.
The corresponding contribution reads typically |
|
|
|
! |
|
|||||||
|
∆mK |
|
|
|
|
|
|
|
||||
|
|
2 |
|
† |
† |
|
|
i |
|
|
(6.94) |
|
|
mK |
α3 |
ij |
Wdi |
Wis Wdj |
Wjs f |
M32 |
, |
M32 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
where mi is the ui squark mass. For a generic W matrix, this is much too large.
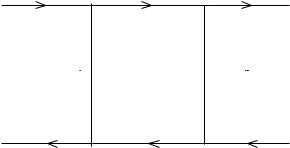
138 Supergravity
S |
Wis |
gluino |
+ |
d |
|
|
Wdj |
|
squark ui |
squark uj |
d |
Wdi+ |
gluino |
Wjs |
S |
|
|
|
¯ |
→ sd¯ amplitude. |
Fig. 6.2 Box diagram of supersymmetric contribution to sd |
||||
We will return in detail to this problem in Chapter 12. Let us say here only that there are several ways of accounting for it:
(i) Universality. To first order, all squarks and sleptons are degenerate. One can then
q q
choose V = V , in which case W = 1 and the supersymmetric box diagram vanishes. Of course, one can only make this assumption at a given scale, of order mP l or MU for supergravity models, and renormalization to low energies will tend to generate nondiagonal terms in the mass matrices and thus FCNC at low energy.
(ii)E ective supersymmetry [79]. FCNC constraints are only crucial for the first two families, whereas the fine-tuning associated with the hierarchy problem concerns mostly the third family in the radiative breaking scenario (since the breaking of
SU (2) × U (1) and thus the scale MZ arises through the top Yukawa coupling). A possible solution is therefore to make the squarks of the first two families heavy (TeV scale), whereas the third family squarks remain relatively light in order to avoid an unwanted fine-tuning. In this case, because of the squark propagators, the function f (m2i /M32, m2j /M32) is very small.
(iii)Quark–squark alignment. If one “aligns” the squark flavors along the quark fla-
vors, that is if the same matrix may diagonalize quark and squark mass matrices,
then V q |
= |
|
|
V q and W = 1. This obviously requires a theory of flavor. It may |
indeed be obtained by imposing flavor symmetries known as horizontal symmetries (in contrast with the ordinary gauge symmetries of the Standard Model which are vertical, i.e. act within a given family of quarks and leptons).
6.8The minimal supergravity model
In the case of the minimal supergravity model, one therefore assumes, besides (6.90), that all scalar masses are equal at unification scale, as well as all A-terms:
mH1 (MU ) = mH2 (MU ) = m0 |
(6.95) |
mQ(MU ) = mU (MU ) = mE (MU ) = m0 |
(6.96) |
mD(MU ) = mL(MU ) = m0 |
(6.97) |
