- •1. Движение. Виды движений. Описание движения. Система отсчета.
- •2. Траектория движения. Пройденный путь. Кинематический закон движения.
- •3. Скорость. Средняя скорость. Проекции скорости.
- •4. Ускорение. Понятие нормального и тангенциального ускорения.
- •5. Вращательное движение. Угловая скорость и угловое ускорение.
- •6. Центростремительное ускорение.
- •7. Инерциальные системы отсчета. Первый закон ньютона.
- •8. Сила. Второй закон Ньютона.
- •9. Третий закон Ньютона.
- •10. Виды взаимодействий. Частицы переносчики взаимодействий.
- •11. Полевая концепция взаимодействий.
- •12. Гравитационные силы. Сила тяжести. Вес тела.
- •13. Силы трения и упругие силы.
- •14. Центр масс системы материальных точек.
- •15. Закон сохранения импульса.
- •16. Момент силы относительно точки и оси.
- •17. Момент инерции твердого тела. Теорема Штейнера.
- •18. Основное уравнение динамики вращательного движения.
- •19. Момент импульса. Закон сохранения момента импульса.
- •20. Работа. Вычисление работы. Работа упругих сил.
- •21. Мощность. Вычисление мощности.
- •22. Потенциальное поле сил. Силы консервативные и неконсервативные.
- •23. Работа консервативных сил.
- •24. Энергия. Виды энергии.
- •25. Кинетическая энергия.
- •26. Потенциальная энергия тела.
- •27. Полная механическая энергия системы тел.
- •28. Связь между потенциальной энергией и силой.
- •29. Условия равновесия механической системы.
- •30. Соударение тел. Виды соударений.
- •31. Законы сохранения для различных видов соударений.
- •32. Линии и трубки тока. Неразрывность струи.
- •33. Уравнение Бернулли.
- •34. Силы внутреннего трения. Вязкость.
- •35. Колебательное движение. Виды колебаний.
- •36. Гармонические колебания. Определение. Уравнения. Примеры.
- •37. Автоколебания. Определение. Примеры.
- •38. Вынужденные колебания. Определение. Примеры. Резонанс.
- •39. Внутренняя энергия системы.
- •40. Первое начало термодинамики. Работа, совершаемая телом при изменении объема.
- •41. Температура. Уравнение состояния идеального газа.
- •42. Внутренняя энергия и теплоемкость идеального газа.
- •43. Уравнение адиабаты идеального газа.
- •48. Распределение Больцмана.
1. Движение. Виды движений. Описание движения. Система отсчета.
Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.
Виды движений:
А) Равномерное
прямолинейное движение материальной
точки:
![]() Начальные условия
Начальные условия
![]()
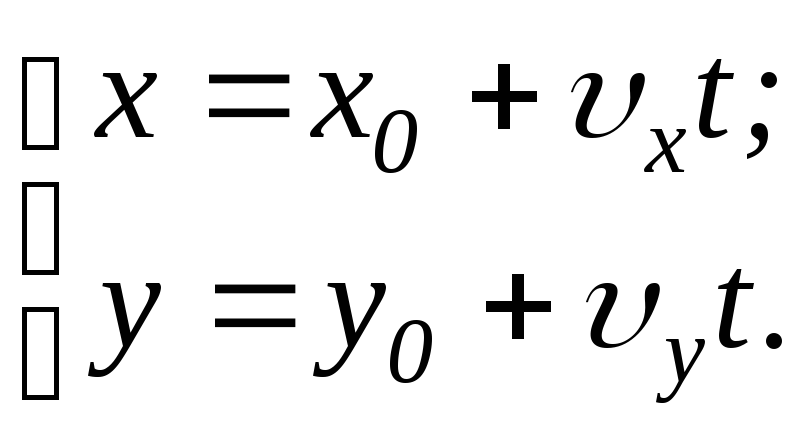
Б) Равноускоренное
прямолинейное движение материальной
точки:![]() .
Начальные условия
.
Начальные условия
![]()
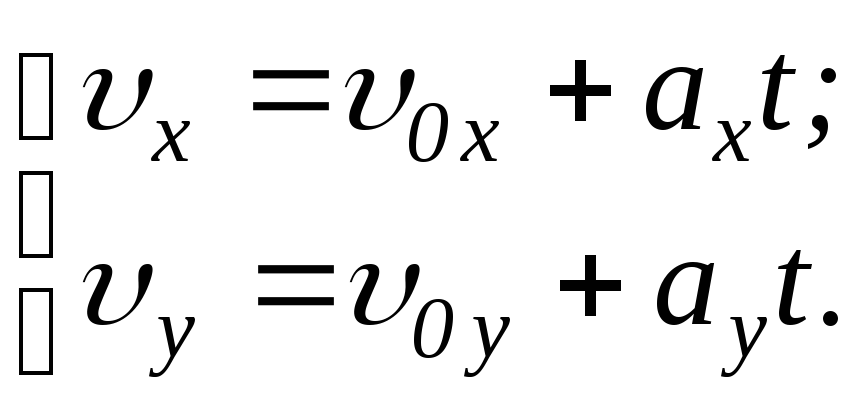
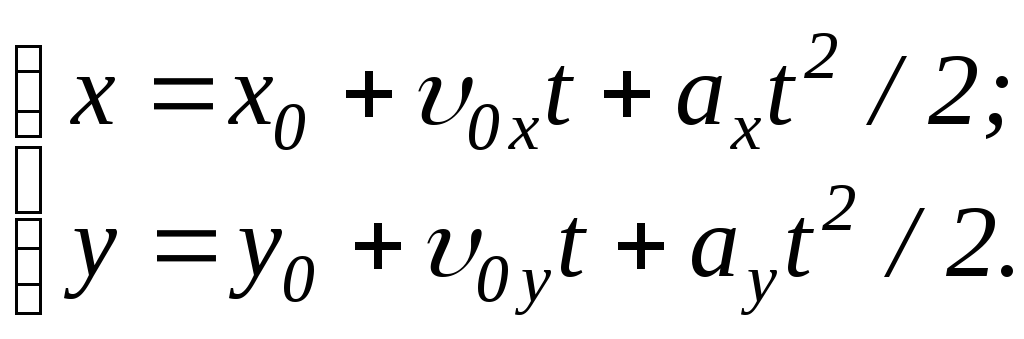
В) Движение
тела по дуге окружности с постоянной
по модулю скоростью:
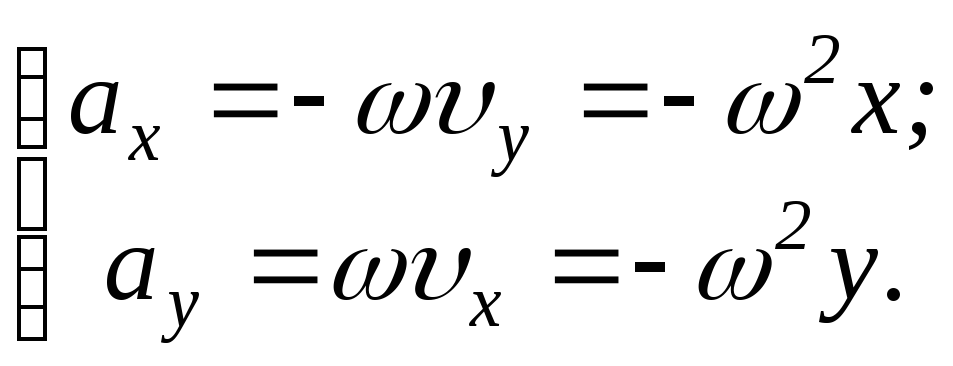
![]()
Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.
![]()
Описания движения. Существуют различные способы описания движения тел. При координатном способе задания положения тела в декартовой системе координат движение материальной точки определяется тремя функциями, выражающими зависимость координат от времени:
x=x(t), y=у(t) и z=z(t).
Эта зависимость координат от времени называется законом движения (или уравнением движения).
При векторном способе положение точки в пространстве определяется в любой момент времени радиус-вектором r=r(t), проведенным из начала координат до точки.
Существует еще один способ определения положения материальной точки в пространстве при заданной траектории ее движения: с помощью криволинейной координаты l(t).
Все три способа описания движения материальной точки эквивалентны, выбор любого из них определяется соображениями простоты получаемых уравнений движения и наглядности описания.
Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.
2. Траектория движения. Пройденный путь. Кинематический закон движения.
Линия, по которой движется некоторая точка тела, называется траекторией движения этой точки.
Длина участка траектории, пройденного точкой при ее движении, называется пройденным путем.
Изменение радиус-
вектора с течением времени называют
кинематическим
законом:
![]() При этом координаты точек будут являться
координатами по времени:x=x(t),
y=y(t)
и z=z(t).
При этом координаты точек будут являться
координатами по времени:x=x(t),
y=y(t)
и z=z(t).
При криволинейном движении путь больше модуля перемещения, так как длина дуги всегда больше длины стягивающей её хорды
Вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиус-вектора точки за рассматриваемый промежуток времени), называется перемещением. Результирующее перемещение равно векторной сумме последовательных перемещений.
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории, и модуль перемещения равен пройденному пути.
3. Скорость. Средняя скорость. Проекции скорости.
Скорость
- быстрота изменения координаты. При
движении тела (материальной точки) нас
интересует не только его положение в
выбранной системе отсчета, но и закон
движения, т. е. зависимость радиус-вектора
от времени. Пусть моменту времени
![]() соответствует радиус-вектор
соответствует радиус-вектор![]() движущейся точки, а близкому моменту
времени
движущейся точки, а близкому моменту
времени![]() — радиус-вектор
— радиус-вектор![]() .
Тогда за
малый промежуток времени
.
Тогда за
малый промежуток времени
![]() точка совершит малое перемещение, равное
точка совершит малое перемещение, равное![]()
Для характеристики
движения тела вводится понятие средней
скорости
его движения:![]() Эта величина является векторной,
совпадающей по направлению с вектором
Эта величина является векторной,
совпадающей по направлению с вектором![]() .
При неограниченном уменьшенииΔt
средняя скорость стремится к предельному
значению, которое называется мгновенной
скоростью
.
При неограниченном уменьшенииΔt
средняя скорость стремится к предельному
значению, которое называется мгновенной
скоростью
![]() :
:![]()
Проекции скорости.
А) Равномерное
прямолинейное движение материальной
точки:
![]() Начальные условия
Начальные условия
![]()
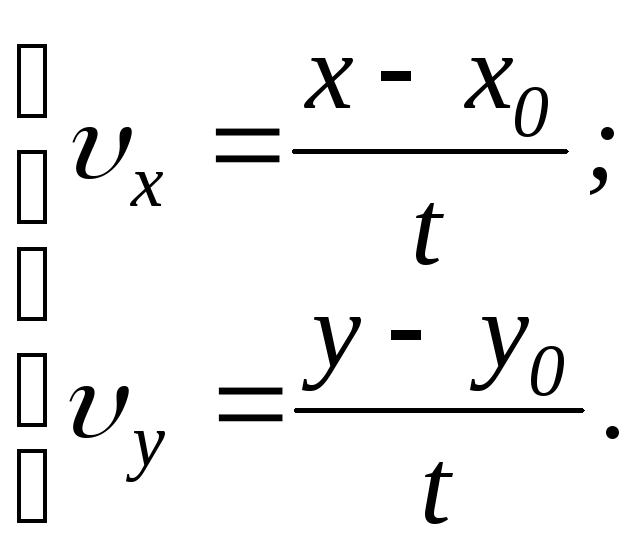
Б) Равноускоренное
прямолинейное движение материальной
точки:![]() .
Начальные условия
.
Начальные условия
![]()
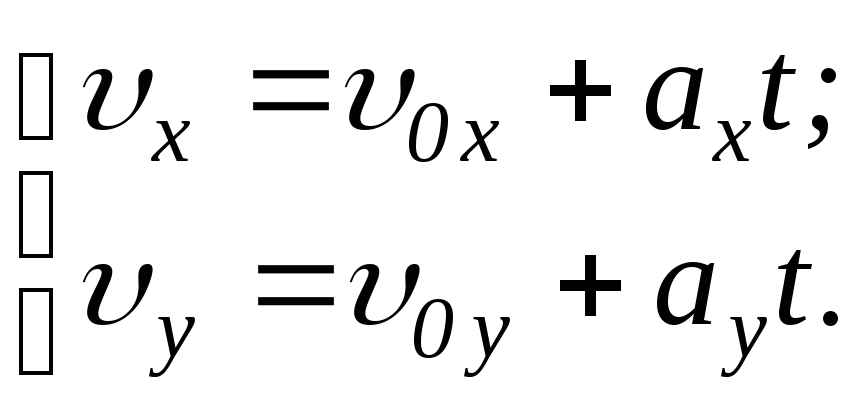
В) Движение
тела по дуге окружности с постоянной
по модулю скоростью: