Тема 4.1. Производная и дифференциал

1. Дифференцируемость функции в точке и в области

1.1. Производная функции

Определение. Пусть функция определена в некоторой окрестности точки . Рассмотрим предел

.

Если он существует, то называется производной функции в точке . Производная обозначается одним из следующих способов:

. (1)

Используется также другой вариант записи формулы (1). Если ввести обозначения:

, (2)

то формула (1) может быть записана в виде

. (3)

1.2. Дифференциал

Определение. Дифференциалом функции в точке называется выражение

. (1)

Если рассматривать независимую переменную как функцию самой себя, то ее дифференциал представляется выражением

(2)

и определение дифференциала поэтому записывают в виде

(3)

В соответствии с формулой (3) дифференциал можно рассматривать как функцию двух независимых аргументов и , причем по второму аргументу эта функция является линейной.

Равенство (3) позволяет рассматривать вариант обозначения производной в виде как частное от деления дифференциала функции на дифференциал аргумента.

Между приращением функции и ее дифференциалом существует тесная связь. Действительно, по свойству предела (1.1.1) отношение отличается от своего предела на бесконечно малую величину при , т.е.

,

где .

Умножим последнее равенство на и с учетом (3) получим

. (4)

Таким образом, приращение функции есть сумма двух слагаемых: дифференциала, являющегося линейной функцией приращения аргумента, и, вообще говоря, нелинейной относительно приращения аргумента части. Покажем, что эта нелинейная часть является бесконечно малой более высокого порядка малости по сравнению с дифференциалом при , если производная не равна нулю. Действительно,

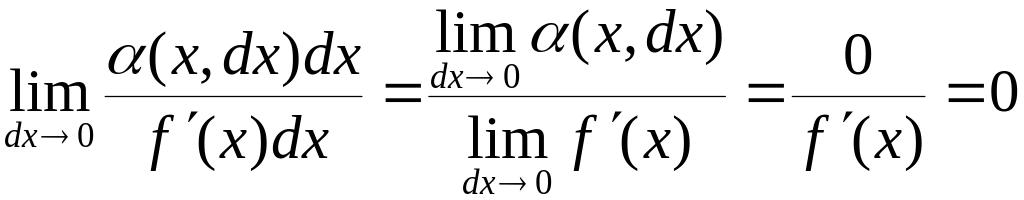. (5)

Следовательно, слагаемое является бесконечно малой величиной более высокого порядка малости, чем дифференциал . Это дает основание называть дифференциал главной линейной частью приращения функции. Из формулы (5) следует, что приращение функции и дифференциал являются эквивалентными бесконечно малыми величинами. Действительно, разделив формулу (4) на с учетом соотношения (5) получим

. (6)

1.3. Связь между существованием производной и непрерывностью функции

Пусть функция имеет производную в точке . Тогда выполняется соотношение (1.2.4), т.е.

. (1)

После переноса в правую часть соотношения (1) и, переходя к пределу, получим

. (2)

Соотношение (2) обозначает непрерывность функции в точке . Таким образом, из дифференцируемости следует непрерывность функции.

2. Геометрический и механический смысл производной

Рассмотрим поведение произвольной функции в окрестности точки . Проведем прямую (см. рис. 1), проходящую через точку с координатами и пересекающую график функции в соседней точке с координатами . Эта прямая называется секущей.

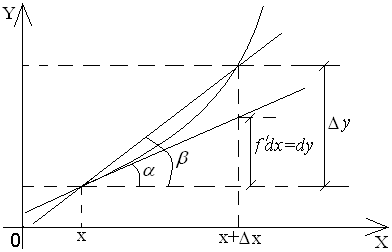
Рис. 1. Геометрический смысл производной

Тангенс угла между секущей и положительным направлением оси абсцисс определяется соотношением

. (1)

При секущая переходит в касательную, а угол переходит в угол наклона касательной к положительному направлению оси абсцисс

. (2)

Соотношение (2) составляет так называемый геометрический смысл производной.

Соотношение (2) позволяет построить уравнение касательной к графику функции в точке . Уравнение прямой в форме с угловым коэффициентом имеет вид

.

Известно, что угловой коэффициент равен тангенсу угла наклона прямой к графику функции, т.е. , а уравнение прямой проходящей через точку с координатами имеет вид

. (3)

Легко получить также уравнение перпендикуляра к кривой в точке . Если угол наклона касательной к кривой считать равным (см. рис. 2), то угол наклона перпендикуляра будет равен . Угловой коэффициент наклона перпендикуляра получается из следующей цепочки соотношений

.

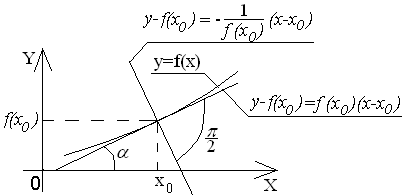
Рис. 2. Касательная и нормаль к кривой в точке с координатами

Заменяя в уравнении (3) угловой коэффициент, получим уравнение перпендикуляра в виде

. (4)

3. Производная суммы, произведения и частного от деления двух функций

Используем свойства предела для доказательства правил дифференцирования.

1.

. (1)

2.

. (2)

3.

(3)

4.

. (4)

4. Производная сложной и обратной функций.

Пусть функция в некоторой окрестности точки является непрерывной, монотонной, а в самой точке - дифференцируемой. Тогда по теореме о непрерывных функциях она имеет обратную . Найдем связь между производными прямой и обратной функций

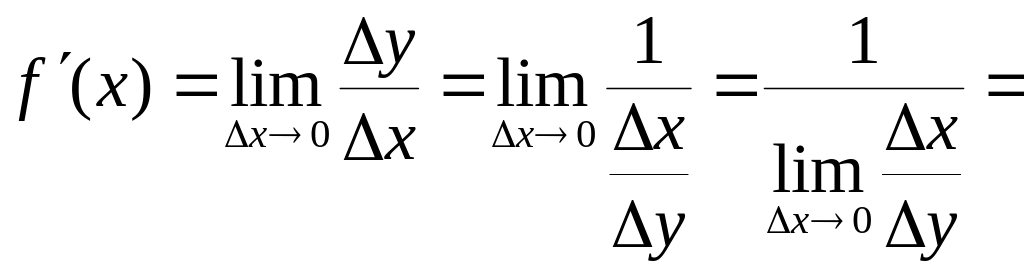
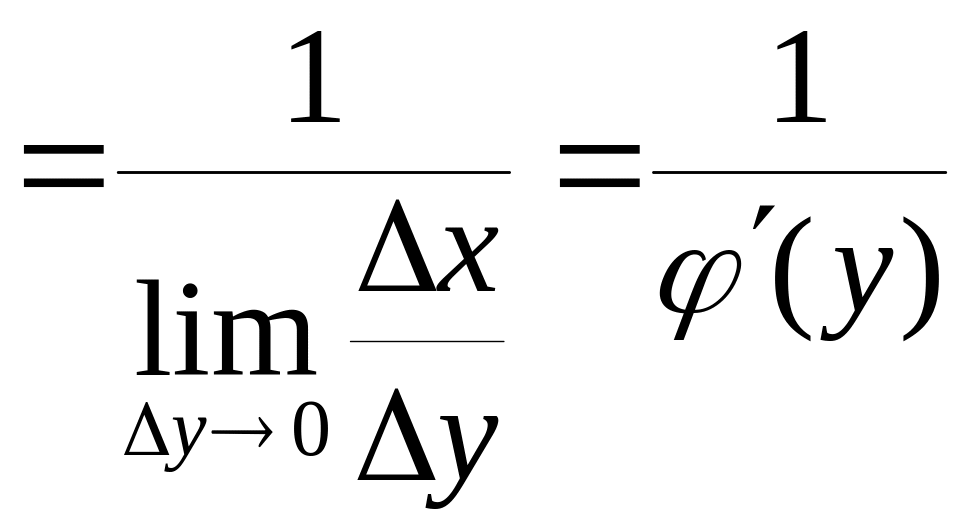. (1)

Формулу (1) следует понимать так, что производные в ее левой и правой части вычисляются при значениях аргументов, связанных между собой соотношениями или .

Определение. Сложной называется функция, которая зависит от своего аргумента, таким образом, что эту зависимость можно представить посредством как минимум одного промежуточного аргумента.

Например, пусть и . Тогда - сложная функция с промежуточным аргументом и независимым аргументом .

Теорема. Если функция имеет производную в точке , а функция имеет производную в точке , где , то сложная функция имеет производную в точке , которая находится по формуле

. (2)

Доказательство

В окрестности точки дадим приращение аргументу . Тогда промежуточный аргумент получит приращение , а функция - приращение .

.

Поскольку в силу существования производной функция является непрерывной в рассматриваемой точке, то при следует, что . Тогда продолжая выкладки, получаем

.