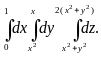Задания для самостоятельного решения:

1. Вычислить повторные интегралы:

а) ;

б) .

2. Вычислить двойной интеграл по данной области :

а) 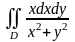, где : , ;

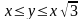б) 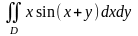, если : , ;

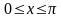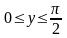в) 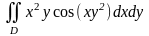, если : , ;

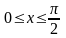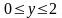г) 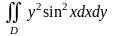, где ограничена линиями , , , ;

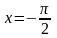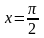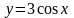д) 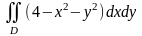, где область ограничена линиями , , , ;

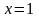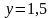е) 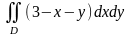, где - круг .

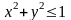3. Вычислить интегральные средние значения данных функций в указанных областях:

а) 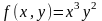, - круг ;

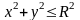б) ; область ограничена линиями , , .

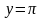4. Найдя подходящую замену переменных, вычислить двойной интеграл, в заданных прямоугольных координатах:

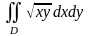, где D ограничена кривыми , , , .

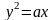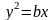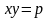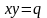
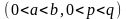5. Вычислить интегралы, переходя к полярным координатам:

а) ;

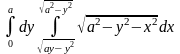б) ;

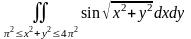в) ;

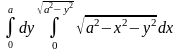г) , где область D ограничена окружностями 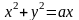, 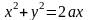и осью ;

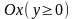д) ;

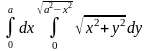е) , где D – круг, ограниченный окружностью ;

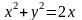ж) , где D ограничена кривыми , , ;

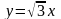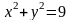з) , где D ограничена окружностью ;

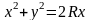и) , где D – круг .

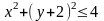6. Вычислить площади фигур, ограниченных кривыми:

а) , ;

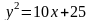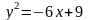б) 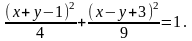Указание.

в) ;

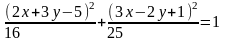г) , , ,

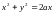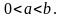
7. Найти массу пластины с поверхностной плотностью

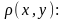
а)

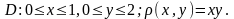
б)

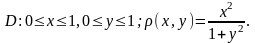
в)

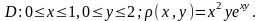
8. Найти координаты центра тяжести фигуры, ограниченной линиями:

а) , , .	б) , .
в) , .

9. Вычислить тройные интегралы в прямоугольных координатах:

а) 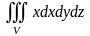, где ограничена цилиндром и плоскостями и ;

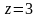б) 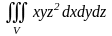, где лежит в первом октанте и ограничена сферой и координатными плоскостями , ;

в) 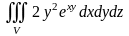, где ограничена плоскостями , , , .

10. Переходя к цилиндрическим координатам, вычислить данные тройные интегралы:

а) 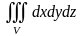, где - ограничена сферой 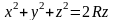, конусом и содержит точку ;

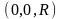б) 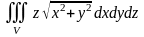, где область задана неравенствами , , ;

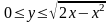11. Вычислить повторные интегралы:

а)

б)

12. Вычислить объемы тел, ограниченных поверхностями:

, , .

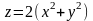13. Вычислить координаты центра тяжести тела, ограниченного параболоидом 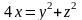и плоскостью .

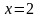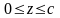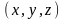14. Вычислить массу прямоугольного параллелепипеда , , , если плотность в точке пропорциональна сумме координат этой точки.

Сыктывкарский государственный университет