§4 Тройной интеграл. Свойства, вычисление, применение

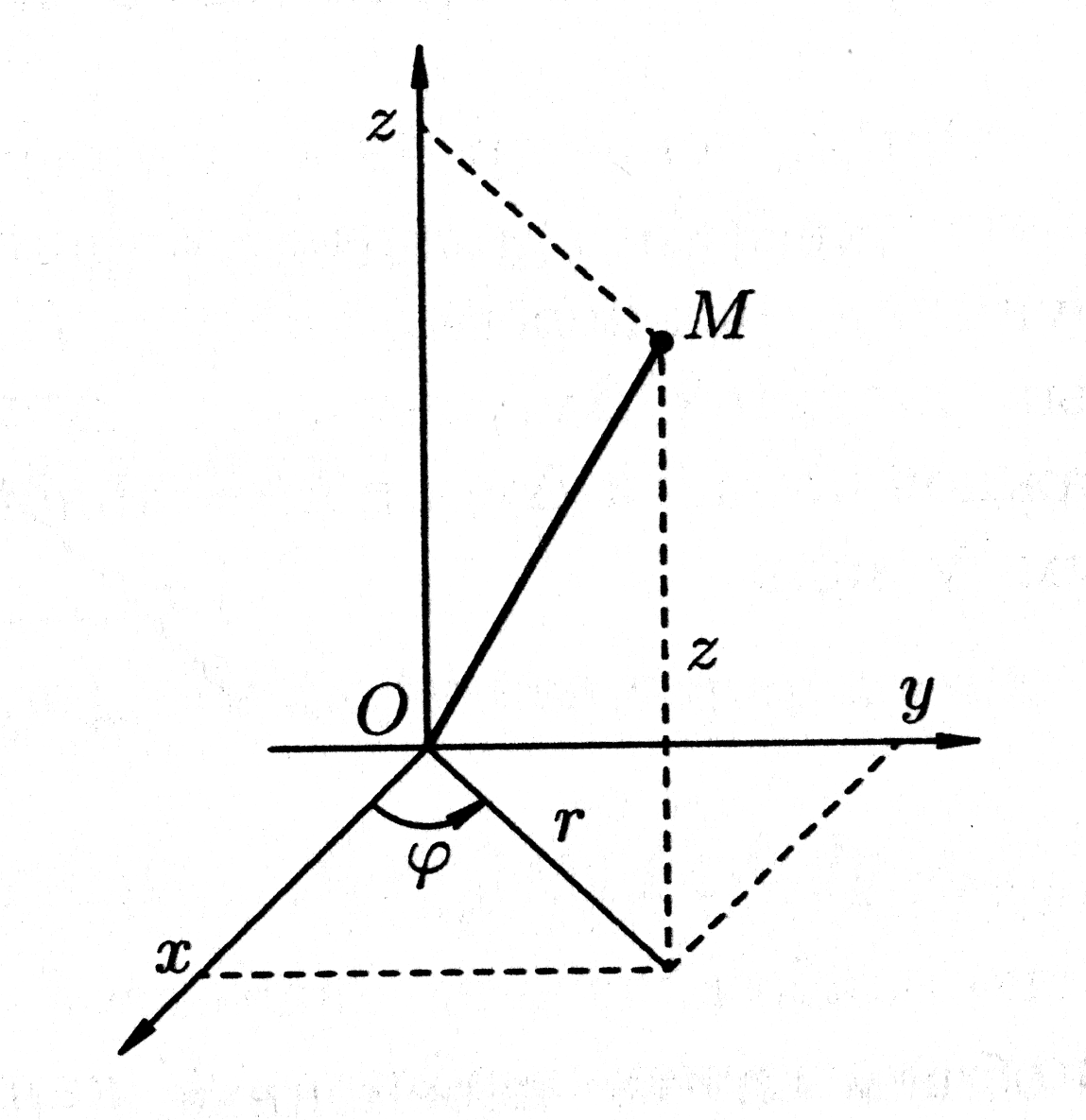
Определение тройного интеграла

Тройной интеграл является аналогом двойного интеграла и вводится для функции трех переменных. Пусть в пространственной области определена и непрерывна функция трех переменных 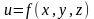. Разобьем область на произвольных областей 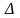v_1, v₂,…, v_n с объемами 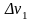, ,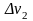…, 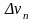затем выберем в каждой области v_i произвольную точку 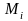и построим интегральную сумму вида

.

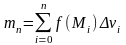Если интегральная сумма 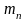имеет предел при стремлении к нулю наибольшего из диаметров областей 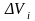, то этот предел называется тройным интегралом и обозначается символом

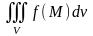и

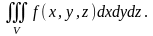
Тройной интеграл обладает свойствами, аналогичными свойствам двойного интеграла (линейность, аддитивность, оценка интеграла, свойство среднего).

Вычисление тройного интеграла

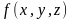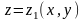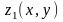Пусть функция трех переменных определена и непрерывна в пространственной области , которая ограничена сверху поверхностью , а снизу - поверхностью , где функции и 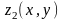определены и непрерывны в области 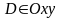(рис. 19). Тогда вычисление тройного интеграла сводится к последовательному (справа налево) вычислению определенного интеграла по переменной 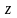(переменные и считаются при этом константами) и двойного интеграла от того, что получится, по области .

В частности, если область представляет собой прямоугольный параллелепипед, определяемый неравенствами , , 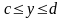, 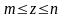то тройной интеграл сводится к трем определенным интегралам:

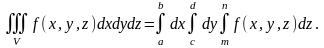
Естественно, можно выбирать другой порядок интегрирования.

Рис. 19.

Рис. 20.

Замена переменных в тройном интеграле

Цилиндрические координаты

Цилиндрические координаты 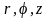(рис. 20) представляют собой обобщение полярных координат на плоскости и связаны с прямоугольными координатами 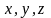формулами

, , .

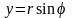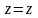Переход к тройному интегралу в цилиндрических координатах осуществляется по формуле

.

В частности, если положить в этом равенстве 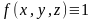, то получим формулу для объема тела в цилиндрических координатах:

.

Сферические координаты

Сферические координаты 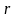, , 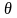связаны с прямоугольными координатами при помощи формул (рис. 21)

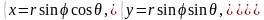
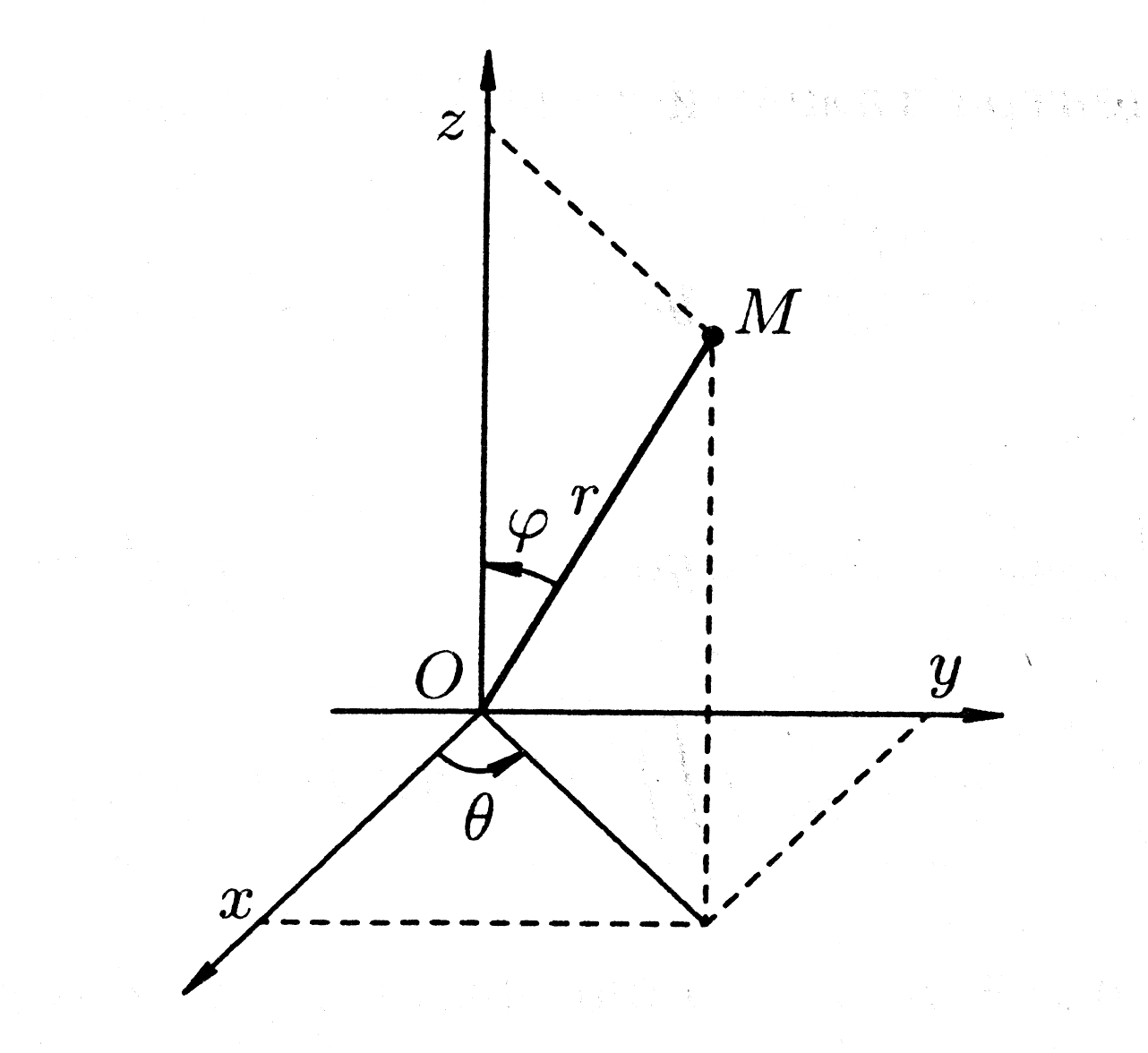
Рис. 21.

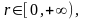
В общем случае переменные , , изменяются в пределах 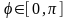, 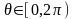. Формула перехода к сферическим координатам имеет вид

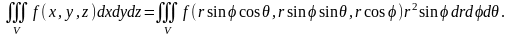
Положив , получим формулу для объема тела в сферических координатах:

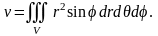
Приложения тройного интеграла

1. Объем тела находится по формуле:

.

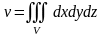2. Масса тела с данной плотностью , где функция непрерывна, вычисляется по формуле

.

3. Статические моменты , , 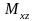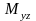тела относительно координатных плоскостей , , соответственно равны

, , ,

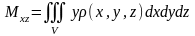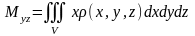где 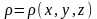- плотность тела .

4. Координаты центра тяжести тела с массой определяются по формулам

, , ,

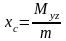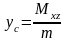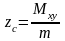или, более подробно:

, , .

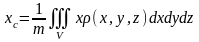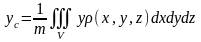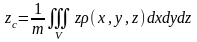В частности, если 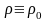(тело однородно), эти формулы упрощаются:

, , ,

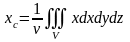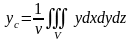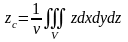где - объем тела .

5. Моменты инерции тела с плотностью относительно координатных плоскостей вычисляются по формулам

, , .

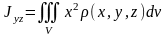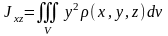Моменты инерции , и тела относительно координатных осей , и соответственно находятся по формулам

, , .

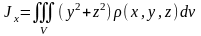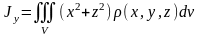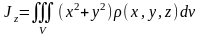Пример 1. Вычислить тройной интеграл

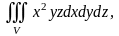
где - область, ограниченная плоскостями , ,

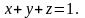
Область (рис. 22) устроена просто, поэтому данный тройной интеграл можно вычислить, используя произвольный порядок интегрирования. Обычно проектируют область на плоскость , принимая полученную проекцию в качестве области (на рис. - треугольник ). Прямая, параллельная оси , пересекает границу в двух точках. Аппликата первой точки равна нулю (точка входа лежит на плоскости , т. е. ), аппликата второй точки равна 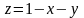(поскольку точка выхода из области лежит на плоскости ). Таким образом,

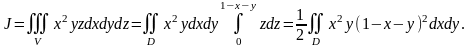
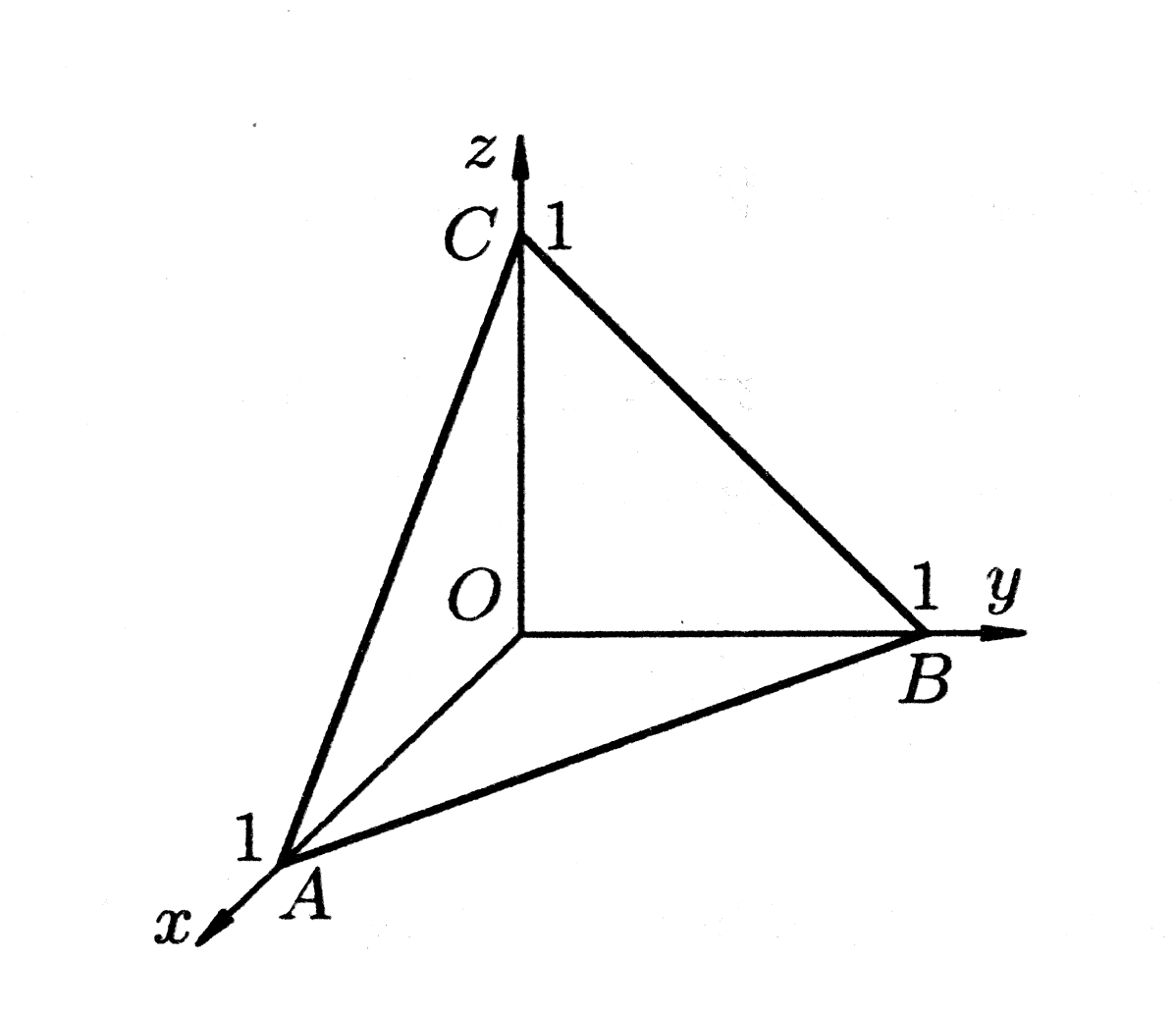
Рис. 22.

Двойной интеграл приводим к повторному.

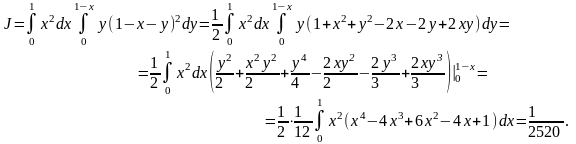
Пример 2. Вычислить тройной интеграл

,

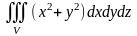если ограничена плоскостью 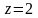и параболоидом .

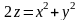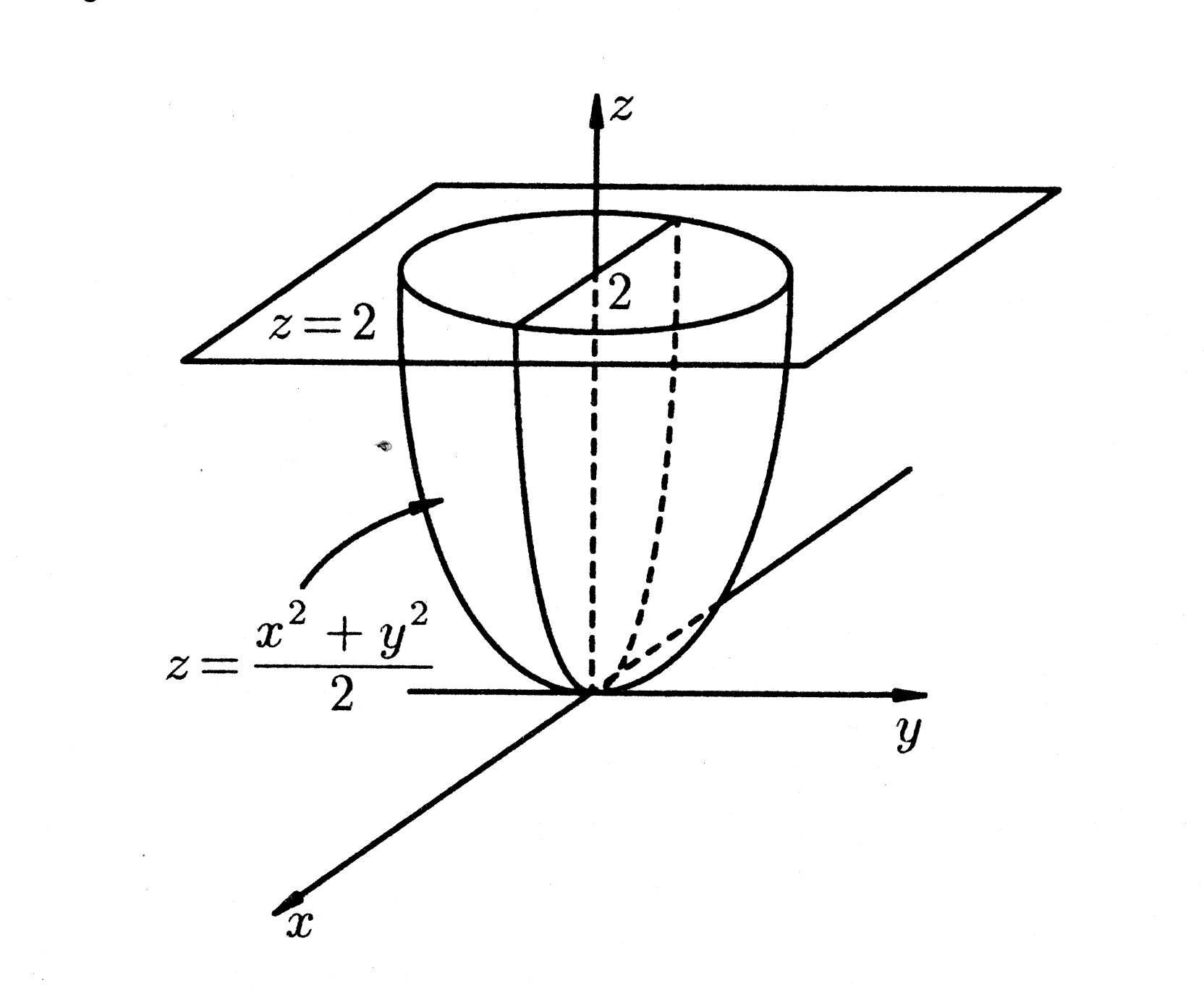
Рис. 23.

Область ограничена сверху плоскостью , а снизу параболоидом 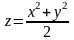(рис. 23). Переходим к цилиндрическим координатам , , . При этом подынтегральная функция преобразуется к виду 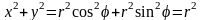. Таким образом,

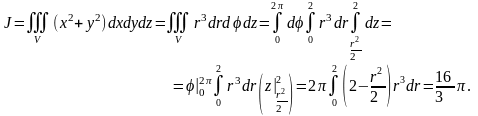
Пример 3. Вычислить повторный интеграл

.

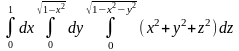Преобразуем повторный интеграл в тройной

,

для этого, исследуем пределы интегрирования в повторном интеграле и восстанавливаем область интегрирования . Она ограничена снизу плоскостью , т. е. плоскостью , а сверху – поверхностью 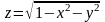, т. е. верхней частью сферы 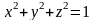. Область лежит в плоскости и ограничена снизу прямой (осью ) и сверху линией 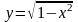, т. е. верхней полуокружностью 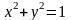. Наконец, проекция на ось - это отрезок . По названным поверхностям построим чертеж области (рис.24), а по соответствующим линиям – область . (рис. 25).

Рис. 24.

Рис. 25.

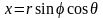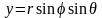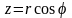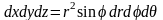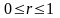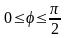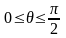Исходя из вида подынтегральной функции и вида области интегрирования, удобнее вычислять интеграл в сферических координатах: , , . При этом , , , . Подынтегральная функция равна

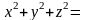
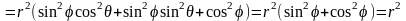
Таким образом,

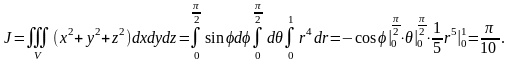
Пример 4. Вычислить объем тела ограниченного сферой 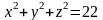и поверхностью параболоида .

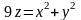Тело расположено над плоскостью между полусферой 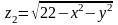и параболоидом (рис. 26).

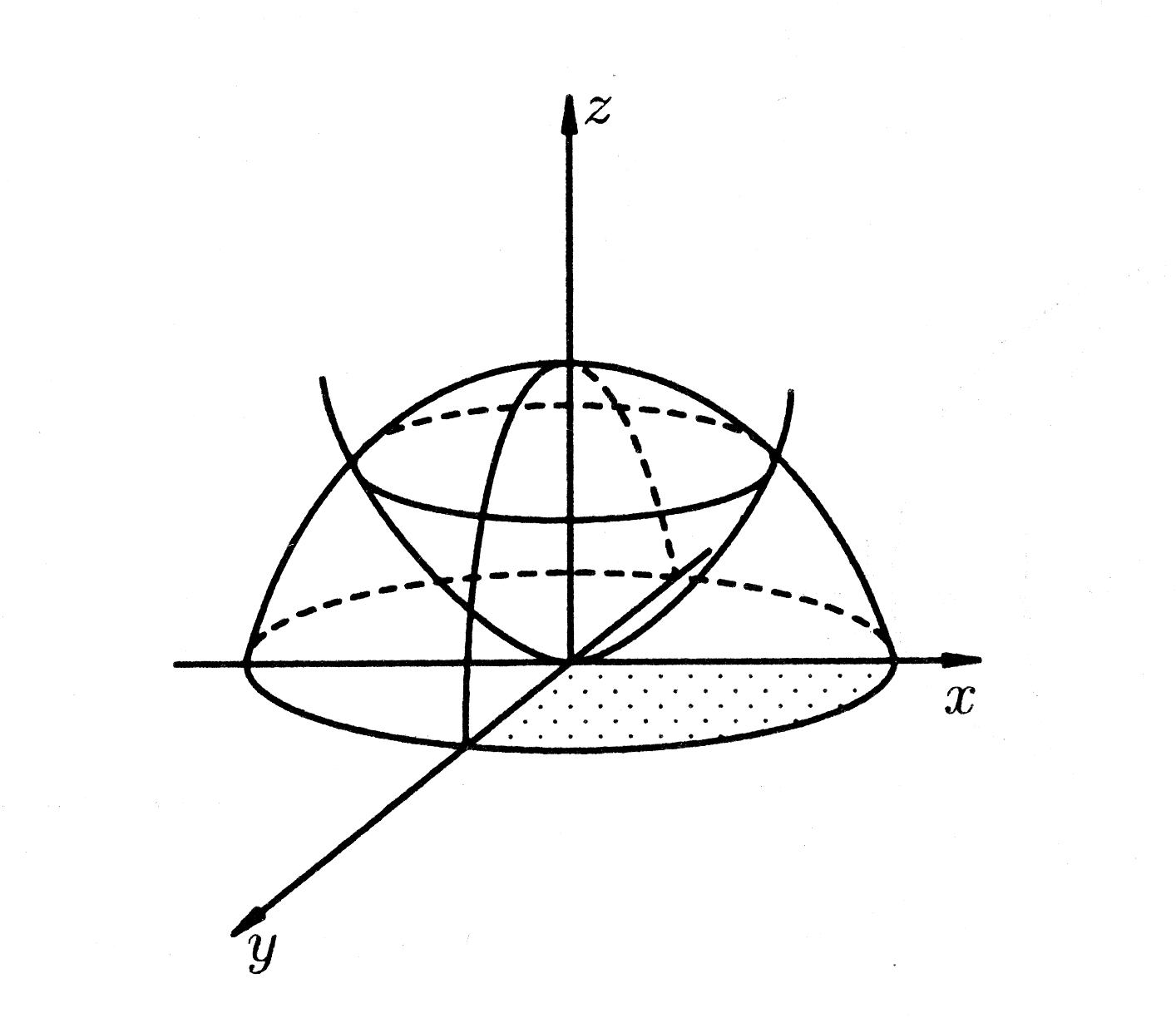
Рис. 26.

Объем тела вычислим по формуле

.

В силу симметрии тела относительно плоскостей и , переходим к цилиндрическим координатам , , и вычисляем объем четвертой части , а результат умножаем на 4.

.

Для дальнейших вычислений надо найти область - проекцию на плоскость пространственной области . Для этого решим систему

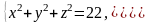
Подставляя (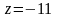 не подходит, т. к. ) во второе уравнение системы, найдем, что сфера и параболоид пересекаются в плоскости по окружности 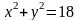. Следовательно, область это четверть круга 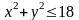( 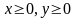), или, в полярных координатах: 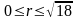, . Таким образом,

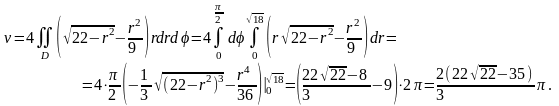
Пример 5. Вычислить координаты центра тяжести верхней половины шара радиуса с центром в начале координат при условии, что его плотность постоянна и равна .

Сделаем сначала рисунок (рис. 27).

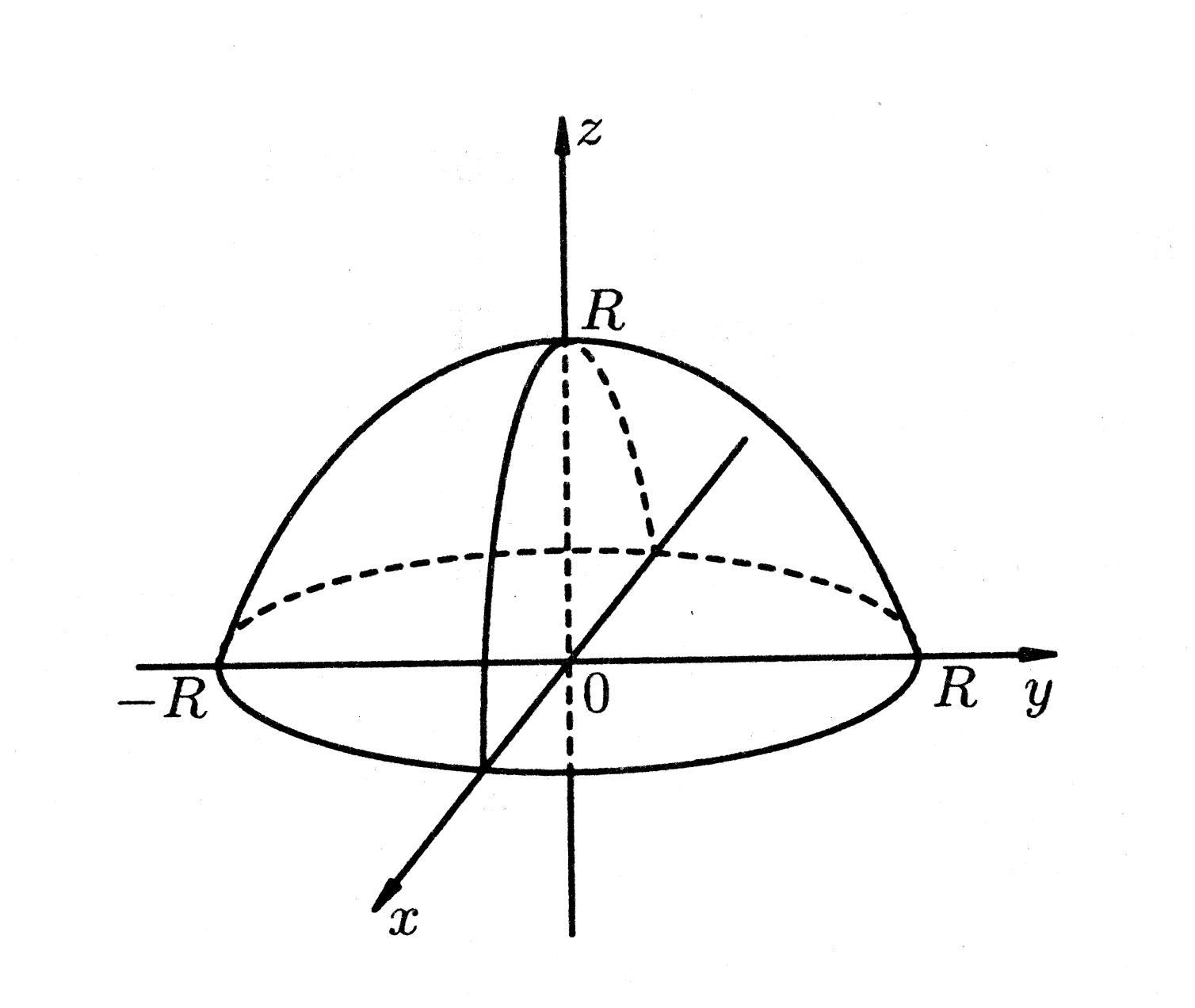
Рис. 27.

Воспользуемся формулами

, , ,

где 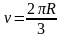- объем полушара.

Подынтегральные функции и в числителях первых двух дробей нечетные, а область интегрирования симметрична относительно соответствующих плоскостей и 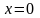. Поэтому 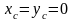. К этому же выводу приходим, исходя из определения 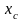и и симметрии тела относительно координатных плоскостей и . Остается вычислить

Для этого переходим к сферическим координатам так же, как в примере 3. Получаем

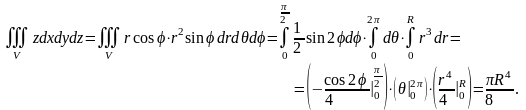
Следовательно, ,

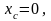
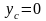Пример 6. Вычислить момент инерции прямого кругового цилиндра радиуса 4 и высоты 6 относительно диаметра сечения, проходящего через центр симметрии цилиндра; плотность цилиндра постоянна и равна .

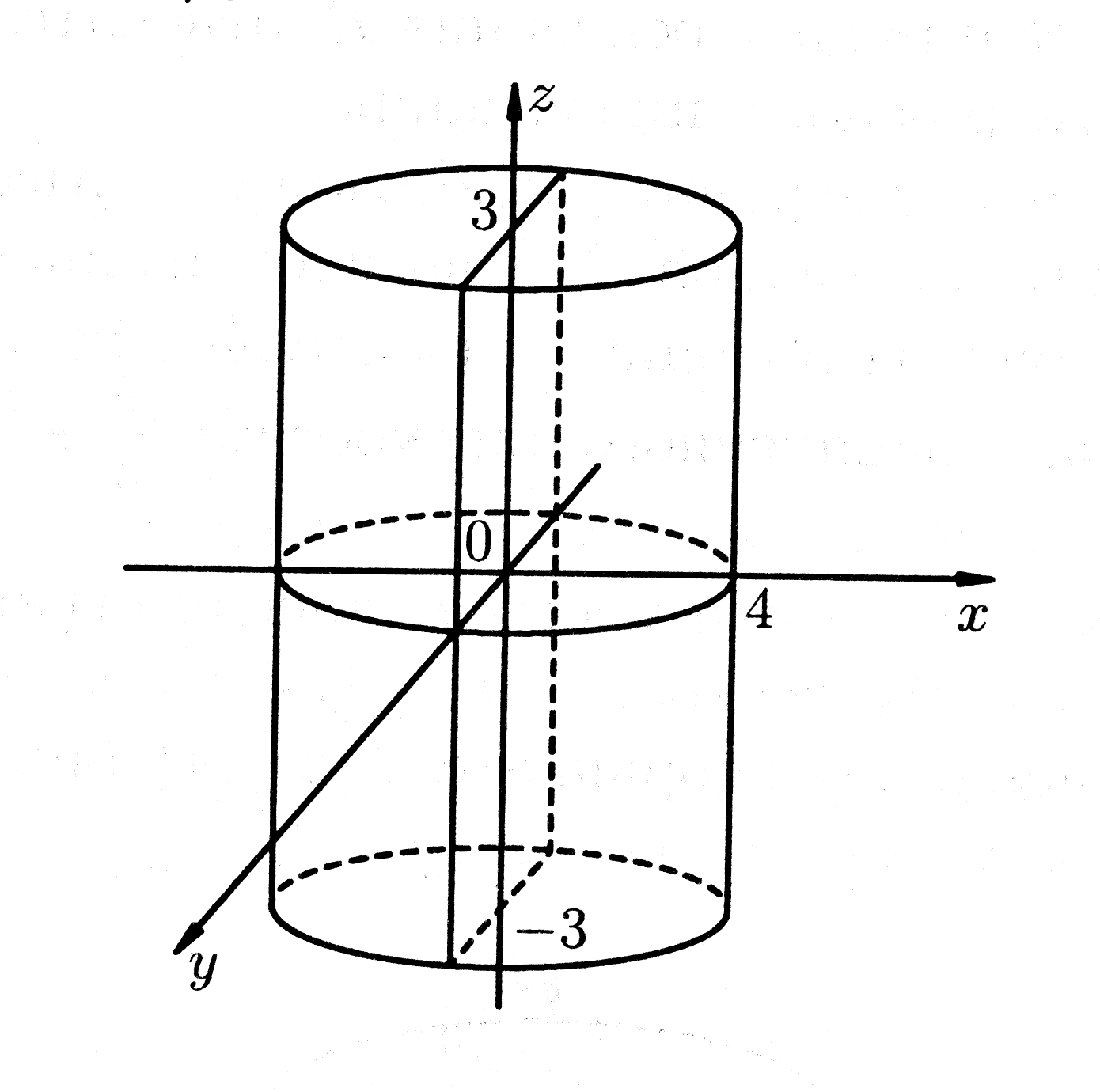
Рис. 28.

Введем прямоугольную систему координат так, как обозначено на рис. 28: ось цилиндра расположена на оси , среднее сечение цилиндра лежит в плоскости . Тогда задача сводится к вычислению - момента инерции цилиндра относительно оси . Используем формулу

,

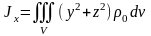где - цилиндр: 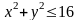, 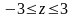. Перейдем цилиндрическим координатам: , , , 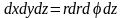, , , . Отсюда и, следовательно,

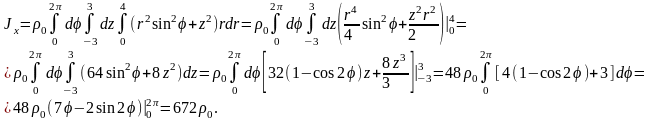
Пример 7. Вычислить объем и массу тела , ограниченного конусом 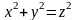и плоскостью 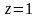, если его плотность (x, y, z) пропорциональна координате z с коэффициентом пропорциональности k, k>0.

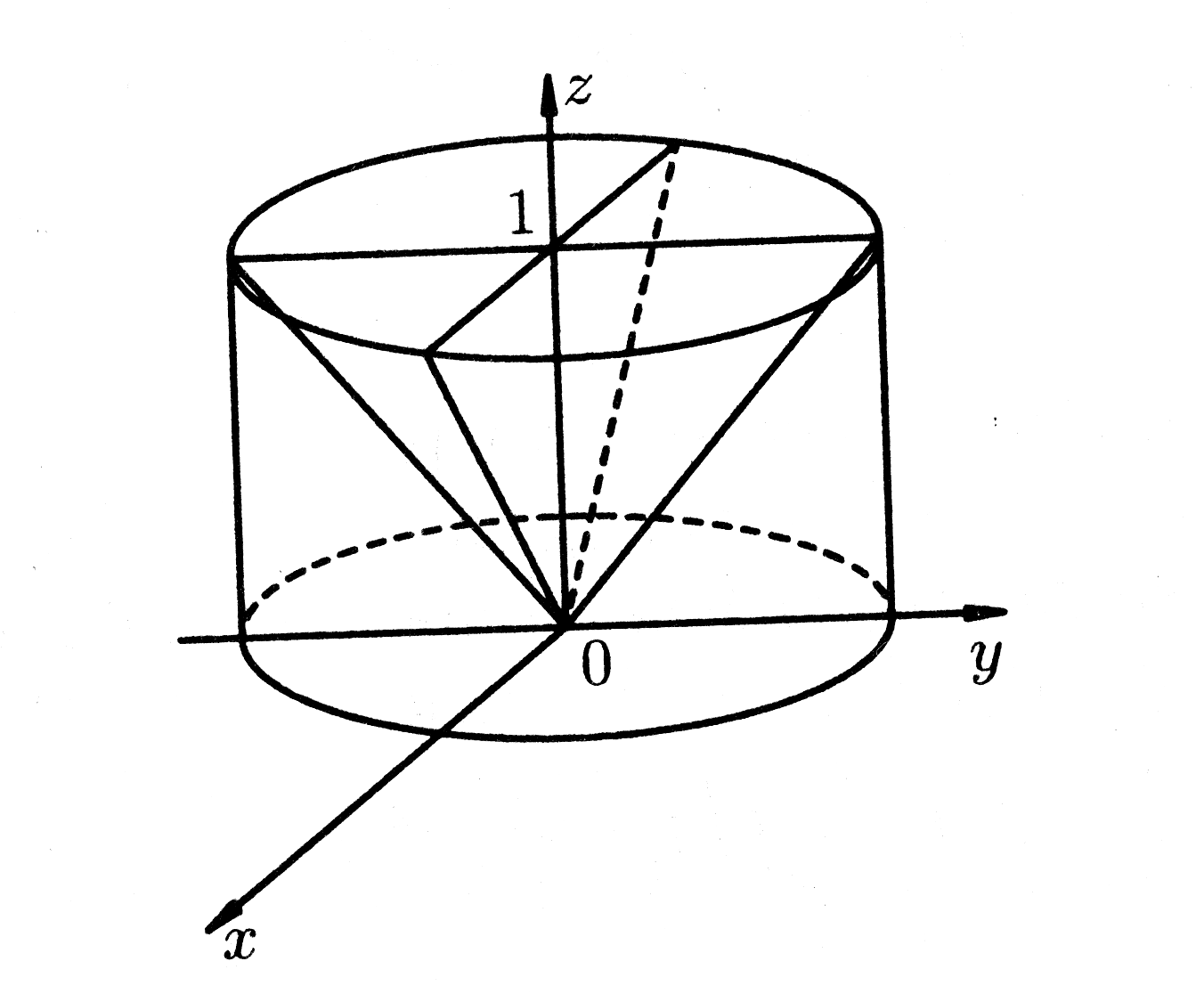
Рис. 29.

Требуемые величины вычислим в цилиндрических координатах: , , , , , 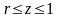, (рис. 29):

;

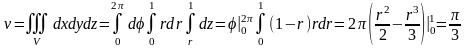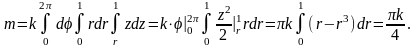
Контрольные вопросы:

1. Дайте определение тройного интеграла от функции по пространственной области.

2. Приведите формулу, по которой осуществляется переход к тройному интегралу в цилиндрических координатах.

3. Приведите формулу для вычисления тройного интеграла в сферических координатах.

4. По какой формуле находится объем тела?

5. Приведите формулу для вычисления массы тела с плотностью .

6. Приведите формулы для вычисления статических моментов тела , , относительно координатных плоскостей , , .

7. Приведите формулы для вычисления координат центра тяжести тела с массой т.

8. Приведите формулы для вычисления моментов инерции тела с плотностью относительно координатных плоскостей.