65. Амплитудная и угловая модуляция гармонического колебания. Ширина спектра при ам и ум.

Амплитудная модуляция (AM) является наиболее простым и очень рас­пространенным в радиотехнике способом заложения информации в высоко­частотное колебание. При AM огибающая амплитуд несущего колебания из­меняется по закону, совпадающему с законом изменения передаваемого со­общения, частота же и начальная фаза колебания поддерживаются неизмен­ными. Поэтому для амплитудно-модулированного радиосигнала общее вы­ражение (1.85) можно заменить следующим:

a(t) = A(t)cos(ω₀t +θ₀) . (1.88)

Характер огибающей А (t) определяется видом передаваемого сообщения.

Основным параметром амплитудно-модулированного колебания является коэффициент модуляции.

Определение этого понятия особенно наглядно для тональной модуляции, когда модулирующая функция является гармоническим колебанием:

s(t) = S₀ cos (Ωt + γ).

Огибающую модулированного колебания при этом можно представить в виде:

. (1.89)

где Ω — частота модуляции; γ — начальная фаза огибающей; k_aм —

к оэффициент пропорциональности; - амплитуда изменения огибающей (рис. 1.8).

Отношение называется коэффициентом модуляции.Таким образом, мгновенное значение модулированного колебания

(1.90)

При неискаженной модуляции (М ≤ 1) амплитуда колебания изме­няется в пределах от минимальной A_min = A₀ (1 - М) до максимальной A_max = A₀ (1 + М)

При передаче дискретных сообщений, представляющих собой чередова­ние импульсов и пауз, модулированное колебание имеет вид последовательности радиоимпульсов, изображенных на рис. 1.9. При этом имеется в виду, что фазы высокочастотного заполнения в каждом из импуль­сов такие же, как и при «нарезании» их из одного непрерывного гармонического колебания. Только при этом условии показанную на рис. 1.9 по­следовательность радиоимпульсов можно трактовать как колебание, моду­лированное лишь по амплитуде. Если от импульса к импульсу фаза изме­няется, то следует говорить о смешанной амплитудно-угловой модуляции.

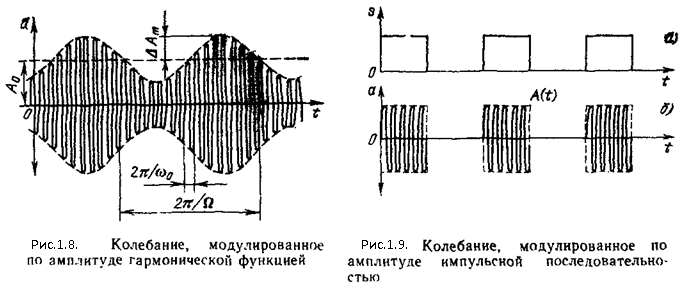
Рис.1.9. Колебание, моделированное по мплитуде импульсной последовательности

1.4.2 Угловая модуляция. Фаза и мгновенная частота колебания

Для простого гармонического колебания

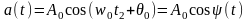
набег фазы за какой-либо конечный промежуток времени от t = t₁ до t =t₂ равен

_. (1.91)

Отсюда видно, что при постоянной угловой частоте набег фазы за какой-ли­бо промежуток времени пропорционален длительности этого промежутка.

С другой стороны, если известно, что набег фазы за время t₂ - t₁ ра­вен , то угловую частоту можно определить как отношение

, (1.92)

если, конечно, имеется уверенность, что в течение рассматриваемого про­межутка времени частота сохраняла постоянное значение.

Из (1.92) видно, что угловая частота есть не что иное, как скорость изменения фазы колебания.

Переходя к сложному колебанию, частота которого может изменяться во времени, равенства (1.91), (1.92) необходимо заменить интегральным и дифференциальным соотношениями

, (1.93)

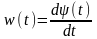. (1.94)

В этих выражениях ω(t) = 2πf(t) — мгновенная угловая частота колеба­ния; f(t) - мгновенная частота.

Согласно выражениям (1.93), (1.94) полную фазу высокочастотного ко­лебания в момент t можно определить как

, (1.95)

где первое слагаемое в правой части определяет набег фазы за время от начала отсчета до рассматриваемого момента t; - начальная фаза ко­лебания (в момент t= 0).

При таком подходе фазу ψ(t) = ω₀t + ϴ(t), фигурирующую в вы­ражении (1.85), следует заменить на ψ(t) = ω₀t +ϴ (t) - ϴ₀.

Итак, общее выражение для высокочас-тотного колебания, амплиту­да которого постоянна, т. е. A (t) = А₀ , а аргумент ψ(t) модулирован, можно представить в форме

. (1.96)

Соотношения (1.94), (1.95), устанавливающие связь между изменения­ми частоты и фазы, указывают на общность двух разновидностей угловой мо­дуляции — частотной и фазовой.

Фаза колебания, a(t) наряду с линейно-возрастающим слагаемым ω₀(t) содержит еще периодическое слагаемое 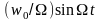. Это позволяет рассматривать a(t) как колебание, модулированное по фазе. Закон этой модуляции является интегральным по отношению к закону изменения ча­стоты. Именно модуляция частоты по закону приводит к модуля­ции фазы по закону . Амплитуду изменения фазы

(1.100)

часто называют индексом угловой модуляции.

При гармоническом модулирующем сигнале различие между ЧМ и ФМ можно выявить, только изменяя частоту модуляции.

При ЧМ девиация ω_д пропорциональна амплитуде модулирующего на­пряжения и не зависит от частоты модуляции Ω.

При ФМ величина ϴ_max пропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляции Ω.

Эти положения поясняются рис.1.13, на котором показаны частотные характеристики величин ω_д и при частотной и фазовой модуляциях. В обоих случаях предполагается, что на вход модулятора подается модули­рующее напряжение с неизменной амплитудой U, а частота _Ω изменяется от _Ωmin до _Ωmax.

При ЧМ ω_д, зависящая, как указывалось выше, только от амплитуды U, будет постоянной величиной, а индекс модуляции т – ω_д/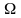 =ϴ_max c увеличением частоты будет убывать (рис. 1.11, а). При ФМ т не зависит от , а ω_д = ϴ_max = m изменяется пропорционально частоте модуляции (рис. 1.11, б).

Рис.1.13. Зависимость индекса θ_max и девиации ω_д от модулирующей частоты

при ЧМ (а) и ФМ (б)

Кроме структуры колебания (при модуляции сложным сигналом) ча­стотная и фазовая модуляции различаются и способом осуществления. При ЧМ обычно применяется прямое воздействие на частоту колебаний генера­тора. При ФМ генератор дает стабильную частоту, а фаза колебания модули­руется в одном из последующих элементов устройства.

Спектральная диаграмма колебания при тональной модуляции показа­на на рис. 1.9. Ширина спектра в этом случае равна удвоенной частоте модуляции 2Ω, а амплитуды колебаний боковых частот не могут превышать половины амплитуды не смодулированного колебания (при М≤ 1).

Аналогичные результаты можно получить при модуляции любым слож­ным сигналом.

Рис.1.11.Спектр колебания при тональной (гармонической) АМ

Заметим, что ширина спектра УМ при т << 1 равна 2 , как и при AM. Этот результат показывает, что при очень малых девиациях ω_д (по сравнению с ) ширина спектра от ω_д не зависит.

Приравнивая это максимальное значение п_тах величине m, приходим к выводу, что полная ширина спектра частотно-модулированного колебания

Но т = ω_д/ , следовательно, при больших индексах модуляции ширина спектра модулированного колебания близка к удвоенной девиации частоты

. (1.109)

Эта полоса частот обозначена в нижней части рис. 1.16.

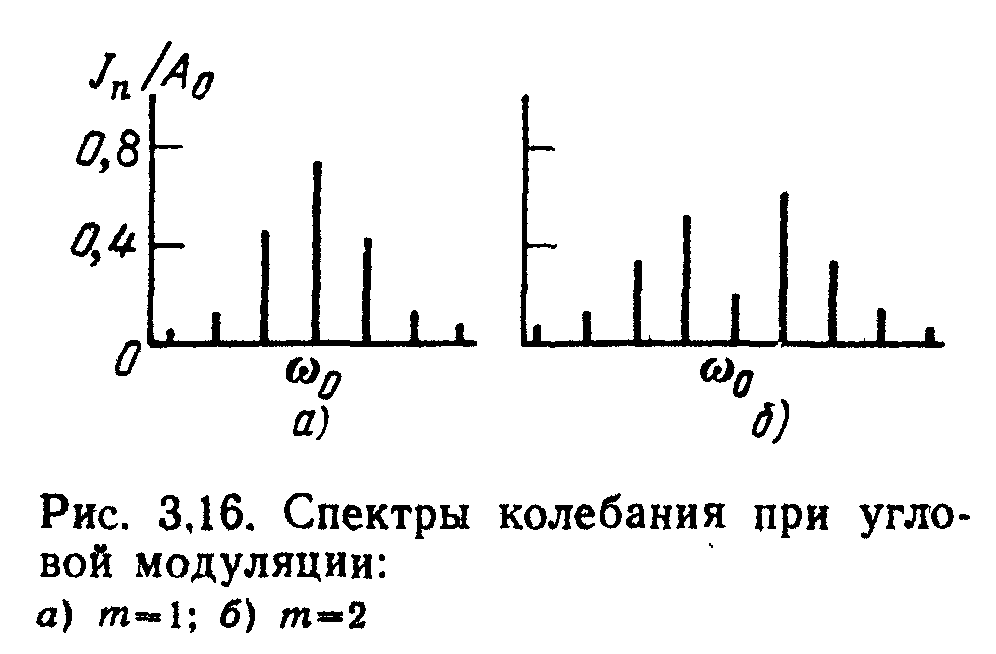
Рис.1.16. Спектры колебания при угловой модуляции: а) m=1; б) m=2

Следует отметить, что в соответствии с опреде­лением т [выражение «модуля­ция с малым индексом» эквивалентно вы­ражению «быстрая модуляция», а выраже­ние «модуляция с большим индексом» экви­валентно выражению «медленная модуляция». Поэтому можно сформулировать следующее положение: при быст­рой угловой модуляции (когда ω_д << ) ширина спектра модулированного ко­лебания близка к значению 2 ; при медленной угловой модуляции (когда ω_д >> ) ширина спектра близка к значению 2ω_д.