60. Обобщенный ряд Фурье, условие ортогональности базисных функций. Понятие нормы базисной функции. Понятие спектра сигнала.

Для теории сигналов и их обработки важное значение имеет разложение заданной функции f(х) по различным ортогональным системам функций . Напомним основные определения, относящиеся к свойствам ортого­нальных систем.

Бесконечная система действительных функций

(1.3)

называется ортогональной на отрезке [а, b], если

при _. (1.4)

При этом предполагается, что

, (1.5)

т. е. что никакая из функций рассматриваемой системы (1.3) не равна тож­дественно нулю.

Условие (1.4) выражает попарную ортогональность функций системы (1.3). Величина

(1.6)

называется нормой функций .

Функция , для которой выполняется условие

(1.7)

называется нормированной функцией, а система нормированных функций 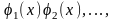в которой каждые две различные функции взаим­но ортогональны, называется ортонормированной системой.

В математике доказывается, что если функции непрерывны, то произвольная кусочно-непрерывная функция f(x), для которой выполняет­ся условие

может быть представлена в виде суммы ряда

. (1.8)

. (1.9)

Ряд (1.8), в котором коэффициенты с_п определены по формуле (1.9), называется обобщенным рядом Фурье по данной системе . Совокупность коэффициентов называется спектром сигнала f(x) в ортогональной системе и полностью определяет этот сигнал.

условие ортогональности: , при ;

квадрат нормы функции:

Применительно к сигналам s(t), являющимся функциями времени, вы­ражение (1.8) в дальнейшем будет записываться в форме

. (1.14)

61. Спектральное представление периодического сигнала. Понятие спектра периодического сигнала.

При разложении периодического сигнала в ряд Фурье по триго­нометрическим функциям в качестве ортогональной системы берут

(1.18)

Или

(1.19)

Интервал ортогональности в обоих случаях совпадает с периодом функции s(t).

Система функций (1.18) приводит к тригонометрической форме ряда Фурье, а система (1.19) — к комплексной форме. Между этими двумя фор­мами существует простая связь.

Воспользуемся сначала ортогональной системой (1.19).

Тогда ряд Фу­рье должен быть записан в форме

. (1.20)

Совокупность коэффициентов с_п ряда Фурье в базисе тригонометриче­ских функций называется частотным спектром периодическо­го сигнала.