Лекция 1
.pdf
vk.com/club152685050 | vk.com/id446425943ИННОВАЦИОННАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА
Термодинамическая вероятность состояния
Состояние системы можно характеризовать
значениями параметров (температура, давление, объем), которые определяют макросостояние системы
совокупностью микросостояний системы, которые определяются распределением частиц по доступным уровням энергии
Число микросостояний, соответствующее данному макросостоянию системы при заданных объеме и внутренней энергии, называют термодинамической вероятностью состояния (W)
Модуль I. Лекция 2. Энергетика химических процессов. Энтропия и энергия Гиббса
vk.com/club152685050 | vk.com/id446425943ИННОВАЦИОННАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА
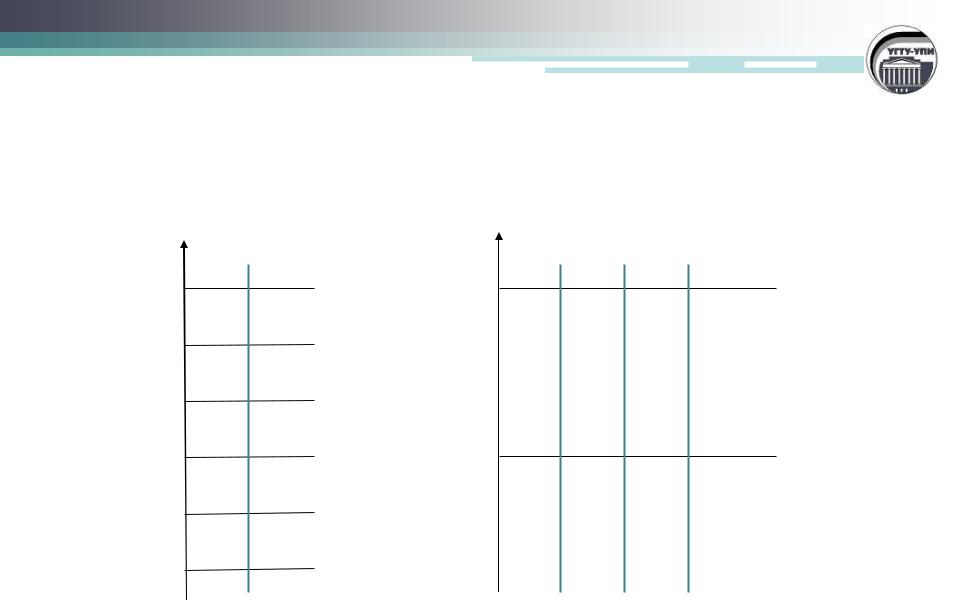
Варианты распределения частиц по уровням энергии
E∑ = 7 усл. ед.
Е |
I |
II |
Е |
I II III IV |
5 |
• |
|
5 |
• |
4 |
• |
4 |
|
|
• |
|
• |
|
|
|
• • • |
||
3 |
3 |
|
|
|
||
• |
|
|
• |
• • |
||
2 |
2 |
|
• • |
|||
1 |
|
1 |
|
• |
• |
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 частицы (W=2) |
3 частицы (W=4) |
Модуль I. Лекция 2. Энергетика химических процессов. Энтропия и энергия Гиббса
vk.com/club152685050 | vk.com/id446425943ИННОВАЦИОННАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА
Энтропия - мера термодинамической вероятности состояния системы
Формула Больцмана:
Sk lnW,
k R NA
k – постоянная Больцмана
R – универсальная газовая постоянная NA – число Авогадро
Размерность энтропии Дж/(моль∙К)
Модуль I. Лекция 2. Энергетика химических процессов. Энтропия и энергия Гиббса
vk.com/club152685050 | vk.com/id446425943ИННОВАЦИОННАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА
Закономерности изменения энтропии
Увеличением энтропии сопровождаются процессы, связанные с увеличением неупорядоченности: нагревание, плавление, сублимация, испарение, растворение твердых веществ; реакции с увеличением объема системы и др.
Уменьшением энтропии сопровождаются процессы, связанные с увеличением упорядоченности: охлаждение, кристаллизация, конденсация веществ; реакции с уменьшением объема системы и др.
Пример. При переходе твердое вещество жидкость газ происходит увеличение неупорядоченности системы и возрастание энтропии:
Вещество |
H2O(к) |
H2O(ж) |
H2O(г) |
S0298, Дж/(моль.К) |
44,8 |
70,1 |
188,7 |
|
|
|
|
Модуль I. Лекция 2. Энергетика химических процессов. Энтропия и энергия Гиббса
vk.com/club152685050 | vk.com/id446425943ИННОВАЦИОННАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА
Второе начало термодинамики:
самопроизвольные процессы в изолированных системах сопровождаются увеличением энтропии
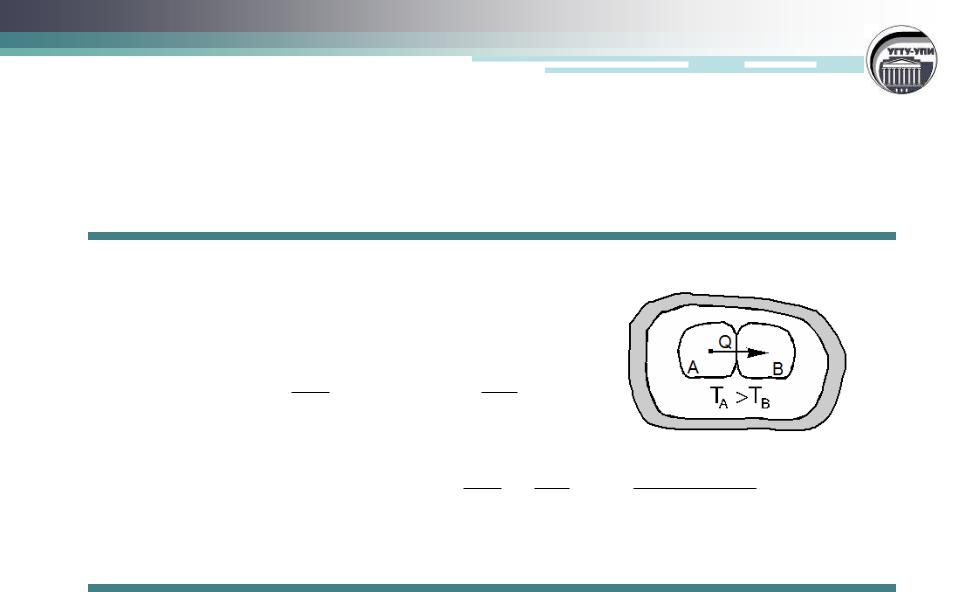
Пример. Теплообмен в изолированной системе между соприкасающимися телами A и B
S |
|
|
|
Q |
; |
||
A |
T |
|
|||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
A |
|
|
S |
S |
A |
|
||||
|
|
|
|
|
|
|
|
|
S |
|
Q |
; |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
B |
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
S |
|
Q |
|
Q |
Q |
(T |
T |
) |
|||
|
|
|
A |
B |
|
||||||
B |
|
|
T |
|
|
T |
|
T T |
|
||
|
|
|
|
|
|
|
|||||
|
|
|
|
A |
|
|
B |
|
|
A B |
|
TA>TB 
S>0, энтропия увеличивается
Условие самопроизвольного прохождения процесса в закрытых системах: T S Q
Модуль I. Лекция 2. Энергетика химических процессов. Энтропия и энергия Гиббса
vk.com/club152685050 | vk.com/id446425943ИННОВАЦИОННАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА
Расчет изменения энтропии химической реакции в стандартных условиях
Энтропия реакции равна разности сумм энтропий продуктов реакции и исходных веществ с учетом стехиометрических коэффициентов:
S |
0 |
n |
S |
0 |
n |
S |
0 |
|
|
|
|||||
|
|
прод прод |
исх |
исх |
|||
S0исх, S0прод - стандартные энтропии исходных веществ и продуктов реакции (справочные данные)
nисх, nпрод - стехиометрические коэффициенты
Модуль I. Лекция 2. Энергетика химических процессов. Энтропия и энергия Гиббса
vk.com/club152685050 | vk.com/id446425943ИННОВАЦИОННАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА
Энергия Гиббса
Самопроизвольное прохождение химической реакции в закрытой системе (р, Т = const) возможно при условии
T S > Qp
Qp = H 
T S > H или H - T S<0
При переходе системы из состояния 1 в состояние 2:
H = H2 – H1 S = S2 – S1
(H2 – H1) – T(S2 – S1) < 0 
(H2 – TS2) – (H1 – TS1) < 0
Mатематическое определение энергии Гиббса: G = H – TS при p, T = const
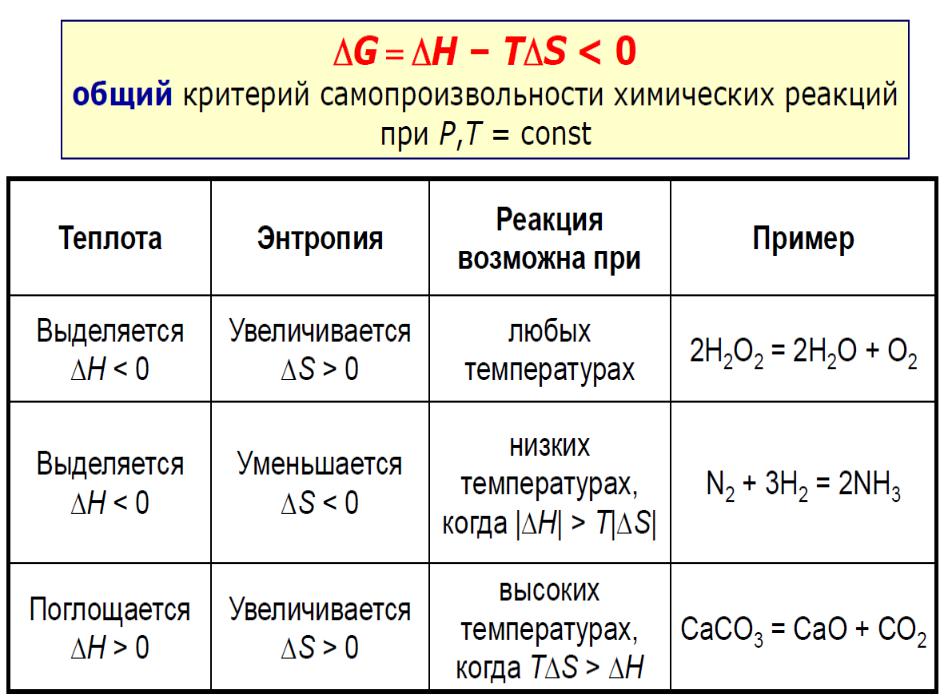
∆G = ∆H – T∆S при р, Т = const
Значение G<0 - условие возможности самопроизвольного прохождения реакции в закрытой системе при р,Т = const
Модуль I. Лекция 2. Энергетика химических процессов. Энтропия и энергия Гиббса
vk.com/club152685050 | vk.com/id446425943ИННОВАЦИОННАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА
Энергия Гиббса – критерий возможности самопроизвольного прохождения химических реакций
Процессы, для которых
G<0 – термодинамически возможныеG>0 – термодинамически невозможные
Для обратимых химических процессов:
G<0 
возможна самопроизвольная прямая
реакция
G>0 
возможна самопроизвольная обратная реакция
G=0 
состояние химического равновесия
(прямая и обратная реакции равновероятны)
Модуль I. Лекция 2. Энергетика химических процессов. Энтропия и энергия Гиббса
vk.com/club152685050 | vk.com/id446425943ИННОВАЦИОННАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА
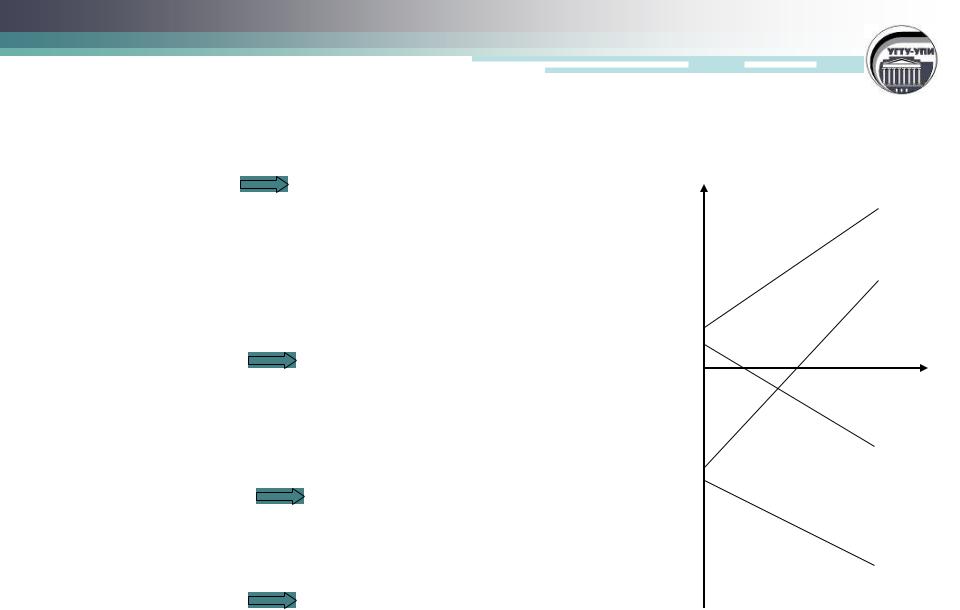
Влияние температуры на направление химической реакции
1. H<0, S<0 |
реакции термодинамически |
|
|
возможны ( G<0) при низких температурах, при |
∆G, кДж |
3 |
|
высоких температурах возможны обратные |
|
|
|
реакции |
|
|
1 |
Пример: N2 + 3H2 = 2NH3 |
|
|
|
2. H>0, S>0 |
реакции термодинамически |
|
|
возможны ( G<0) при высоких температурах, при |
|
Т, К |
|
низких температурах возможны обратные реакции |
|
||
|
|
||
Пример: CaCO3 = CaO + CO2 |
|
2 |
|
3. H>0, S<0 |
G>0, реакции при любых |
|
|
температурах термодинамически невозможны |
|
|
|
Пример: N2 + 2O2 = 2NO2 |
|
4 |
|
4. H<0, S>0 |
G<0, реакции при любых |
|
|
|
|
||
температурах термодинамически возможны.
Пример: 2C + O2 = 2CO
Модуль I. Лекция 2. Энергетика химических процессов. Энтропия и энергия Гиббса
vk.com/club152685050 | vk.com/id446425943