7

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Рязанский государственный радиотехнический университет

Кафедра эконометрики и математического моделирования

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ

К САМОСТОЯТЕЛЬНОЙ РАБОТЕ

ПО ДИСЦИПЛИНЕ “ЭКОНОМЕТРИКА”

для студентов групп П-130, П-131

Заведующий кафедрой ЭиММ РГРТУ

профессор Чураков Е.П.

Рязань 2012

1. Общие положения

Тема самостоятельной работы: проведение корреляционного и регрессионного анализа зависимости товарооборота от торговой площади и среднего в день числа посетителей.

Цель самостоятельной работы: практическое изучение и применение основных методов корреляционного и регрессионного анализа.

Объект исследования: товарооборот 12 магазинов.

Исходные данные к работе:

Годовой товарооборот магазинов (в млн. Р.)

Y=[19.7 38 40.9 41 56.2 68.5 75 89 91.1 91.2 99.8 108.5]^T+z ,

где ^T – символ транспонирования и z- Ваш номер в списке группы;

торговая площадь (тыс.кв. м.)

X1=[0.24 0.31 0.55 0.48 0.78 0.98 0.94 1.21 1.29 1.12 1.29 1.49]^T+ ;

среднее в день число посетителей (тыс.чел.)

X2=[8.2 10.2 9.3 11 8.5 7.5 12.3 10.8 9.9 13.7 12.3 13.9]^T+ .

Цель исследования: выявить, аналитически описать и обосновать зависимость товарооборота магазинов от величины торговой площади и среднего числа покупателей.

Регрессионные модели, используемые в процессе выполнения работы:

Регрессионная модель	Номер в задании
y= 0+ 1x1+ 2x2+ 3x12+	1
y= 0+ 1x1+ 2x2+ 3x22+	2
y= 0+ 1x1+ 2x2+ 3x1x2+	3
y= 0+ 1x1+ 2x2+ 3 +	4
y= 0+ 1x1+ 2x2+ 3 +	5

В этой таблице : y –товарооборот; x₁ –торговая площадь; x₂ – среднее число посетителей; _i, i=0, 1, 2, 3, – параметры регрессии,  – стохастическая составляющая.

2. Порядок выполнения работы и указания

1. В соответствии с ниже приведенной таблицей вариантов заданий по Вашему номеру z в составе группы определите регрессионную модель, подлежащую последующему исследованию, и исходные данные Y, X1, X2 к работе.

	Модель
	1	2	3	4		5
	1	2	3	4		5
	6	7	8		9	10
	11	12	13	14		15
	16	17	18	19		20
	21	22	23	24		25
	26	27	28	29		30
	31	32	33	34		35
	36	37	38	39		40

2. Постройте диаграммы рассеяния годового товарооборота в зависимости от торговой площади и среднего числа посетителей.

3. Проверьте наличие зависимости переменной y от аргументов x₁, x₂. Для упрощения анализа на начальном этапе исследования выявите наличие (или отсутствие) этой зависимости отдельно по каждой экзогенной переменной x₁ и x₂. Соответствующий анализ проводится по следующей схеме.

На основании экспериментальных данных находятся эмпирические (выборочные) коэффициенты парной корреляции и эндогенной переменной y с каждой из экзогенных переменных x₁ и x₂ :

= ,

k=1,2. (1)

С помощью вычисленных эмпирических коэффициентов корреляции находятся соответствующие значения случайной величины

_k= t(n-2), k=1,2, (2)

распределенной по закону Стьюдента с n-2 степенями свободы и используемой для выявления значимости каждого из парных коэффициентов корреляции. Для анализа значимости задаются доверительной вероятностью 1- и

по таблицам [2] или с помощью Mathcad-программы находят 100/2-процентную точку w_100/2 распределения Стьюдента с n-2 степенями свободы. Если окажется, что при определенном k _k>w_100/2, то с вероятностью  ошибиться гипотеза об отсутствии корреляционной связи величины y и соответствующей этому k экзогенной переменной отвергается как несоответствующая экспериментальным данным, а соответствующий выборочный коэффициент парной корреляции признается значимым. При противоположном неравенстве с вероятностью 1- считается справедливой гипотеза об отсутствии корреляционной связи эндогенной переменной и k-й экзогенной переменной как не противоречащая экспериментальным данным, а соответствующий этому k выборочный коэффициент корреляции принимается незначимым. Критическую точку в Mathcad можно найти, например, с помощью функции

.

4. Постройте доверительные интервалы для истинных коэффициентов корреляции r_yk, k=1,2, воспользовавшись следующим определением: с доверительной вероятностью 1- выполняется

thc_k<r_ykthd_k, k=1,2, (3)

где использованы обозначения

c_k,d_k=0.5ln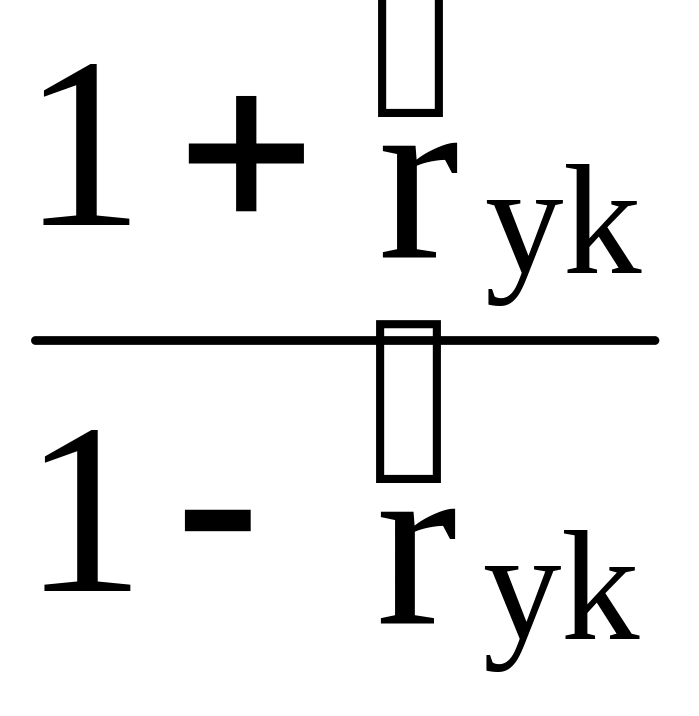 u_/2 - , (4)

th = – гиперболический тангенс,

u_/2 – /2квантиль стандартного гауссова распределения N(0, 1), который можно найти из таблиц [2] или вычислить в Mathcad’е

.

5. Пункты 3, 4 задания выполните при условии устранения из парных выборочных коэффициентов корреляции влияния мешающего параметра, соответствующего этому коэффициенту парной корреляции. С этой целью по подобной (1) формуле следует рассчитать эмпирический коэффициент корреляции между экзогенными переменными x₁ и x₂. Далее с использованием выражений

, (5)

находятся очищенные от влияния мешающей экзогенной переменной частные эмпирические коэффициенты корреляции и эндогенной и экзо-

генных переменных. Проверку гипотезы H₀ о некоррелированности эндогенной и экзогенных переменных (истинный коэффициент частной корреляции равняется нулю) выполните с использованием статистики (2). Доверительные интервалы для истинных коэффициентов корреляции _y1 и _y2 находятся подобным (3), (4) образом, но в выражениях (2), (4) и при вычислении критических точек объем n выборки следует заменить на n-1. Сопоставьте результаты выполнения этого пункта с предыдущими результатами и дайте объяснение возникающим различиям в случае обнаружения таковых.

В процессе выполнения работы доверительная вероятность 1-=0.95 для всех вариантов.

6. Используя метод наименьших квадратов, найдите МНК–оценку вектора регрессионных параметров в соответствии с Вашим вариантом задания. В матрично-векторных обозначениях совокупность наблюдений эндогенной переменной задается выражением

,

а оценка находится из условия

и определяется соотношениями

=(X^TX)^-1X^Ty,

= , = , = , n=12. (6)

Функция (x₁,x₂) в составе матрицы определяется последним слагаемым в выражении регрессионной модели, соответствующей Вашему варианту задания; x_1i, x_2i – значения экзогенных переменных.

7. Используя любой вариант выражения

= , (7)

где - i-я строка матрицы , m+1 – размерность вектора , ||c|| - норма вектора c, - i-й компонент вектора , определите величину , являющуюся мерой разброса экспериментальных данных y_i относительно значений, “предсказанных” регрессионной моделью (оценка дисперсии стохастической составляющей в составе экспериментальных данных).

8. Вычислите коэффициент детерминации K_d², соответствующий Вашим экспериментальным данным, воспользовавшись определением

K_d²= , (8)

где использованы обозначения

y_i, = [1 1 ... 1]^TRⁿ.

Прокомментируйте содержательный смысл этого коэффициента.

9. Подтвердите более тщательным образом наличие зависимости товарооборота от величины торговой площади и числа посетителей. Для этого сформулируйте соответствующие гипотезы и вычислите величину

z =  F(m, n-m-1), (9)

распределенную по закону Фишера с m степенями свободы числителя и n-m-1 степенями свободы знаменателя. Пусть w_100 – 100% -я точка F-распределения с числом степеней свободы числителя m и знаменателя n-m-1, которая находится по таблицам [2] или с помощью Mathcad-программы

Тогда если окажется z< w_100, то с вероятностью 1- принимается гипотеза об отсутствии связи между y и x₁, x₂ . При противоположном неравенстве с вероятностью  ошибиться эта гипотеза отвергается. В пояснительной записке дайте подробную аргументацию этого решения.

10. Воспользовавшись выражением

K = , (10)

найдите ковариационную матрицу K ошибок оценок . Объясните смысл этой матрицы.

11. Проверьте справедливость гипотезы ₃=0 против альтернативы ₃ 0. Эту гипотезу с доверительной вероятностью 1- следует признать, если

, (11)

где ^w_100/2 ^– 100/2-процентная точка распределения Стьюдента с n-m-1 степенями свободы, – соответствующий элемент матрицы K. При противоположном неравенстве эта гипотеза отвергается с вероятностью  ошибиться.

12. Если принята гипотеза ₃=0, следует надлежащим образом откорректировать регрессионную модель и заново провести расчеты в соответствии с пп. 6 – 10.

13. Постройте (1-)-доверительные интервалы для истиных параметров ₁ и ₂ в скорректированном уравнении регрессии. Соответствующие интервалы описываются выражением

_i+u_/2 < _i _i-u_/2 , i=1,2, (12)

где u_/2 – /2-квантиль распределения Стьюдента с n-m-1 степенями свободы, величина находится по матрице K. В Mathcad’е квантиль возвращается с применением функции

Объясните смысл интервала (12).

14. Используя построенную скорректированную регрессионную модель, выясните, на сколько изменится товарооборот магазина, если площадь торговых залов увеличится на 100 кв. м., а количество посетителей уменьшится на 500 человек.

15. Поступая аналогичным п.6 образом, постройте две линейные регрессионные модели, связывающие товарооборот самостоятельно с каждой экзогенной переменной (торговая площадь и число посетителей). Графически отразите полученные зависимости на диаграммах рассеяния, построенных в п.2.