X изменяется от -2 до 2 с шагом 0.25;
y изменяется от 1.2 до 5.2 с шагом 0.2.
Задача 2 (вариант 25)
Дана матрица:
Вывести на печать исходную и транспонированную
матрицу.
Задача 3 (вариант 25)
Элементы матрицы определяются по формуле:
a[i,j]=2i2 + j2 + 3
Найти сумму элементов тех строк матрицы A, первые элементы которых удовлетворяют неравенству: 5<=cTg(a[i,j])<=8.1
На печать вывести матрицу A и полученную сумму.
Задача 4 (вариант 25)
Дана матрица:
Подсчитать и вывести на печать число элементов, равных нулю.
Задача 5 (вариант 25)
Даны два массива: X=(3.2, 0.2), Y=(5.1, -0.01, 19.2).
Вычислить элементы матрицы Z по правилу:
и найти ее минимальный элемент.
Задача 6 (вариант 25)
Дана матрица:
Найти номера строк, в которых, положительных элементов больше, чем отрицательных. Напечатать найденные номера строк и число положительных элементов в этих строках.
Задача 7 (вариант 25)
Дана матрица:
Выяснить, является ли матрица симметрической.
Пояснение: матрица называется симметрической, если транспонированная матрица равна исходной.
Задача 8 (вариант 25)
Для заданного x сформировать матрицу вида:
Задача 1 (вариант 26)
Вычислить таблицу значений функции:
,
для z , изменяющегося от 1 до 2 с шагом 0.1.
Значения X заданы последовательностью:
X=(-2.5, 2.1, -0.58, 1.4, -2.7).
Печать таблицы оформить с заголовком:
x z y
Задача 2 (вариант 26)
Дана матрица:
Все отрицательные элементы матрицы увеличить в 2 раза, а все неотрицательные элементы заменить на 0.5. На печать вывести матрицу A с преобразованными элементами.
Задача 3 (вариант 26)
Дана матрица:
Вычислить величину y=Ln S1 + сTg │S2│ , где S1 - сумма квадратов элементов матрицы A; S2 - сумма отрицательных элементов матрицы A.
Задача 4 (вариант 26)
Дана матрица:
Вычислить отношение суммы положительных элементов к сумме отрицательных элементов заданной матрицы.
Задача 5 (вариант 26)
Дана матрица:
Вывести на печать индексы максимального элемента данной матрицы.
Задача 6 (вариант 26)
Элементы матрицы A(4,4) определяются по формуле:
a[i,j]=сTg(i+j).
Найти сумму минимальных элементов ее столбцов.
Задача 7 (вариант 26)
Дана матрица:
Найти норму заданной матрицы.
Пояснение: нормой называется число, равное максимальному из сумм модулей элементов матрицы, расположенных в ее строках.
Задача 8 (вариант 26)
Дана матрица с четным числом строк:
Поменять местами первую и последнюю строки, вторую
и предпоследнюю строки и т.д.
Задача 1 (вариант 27)
Вычислить значения функции:
,
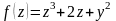где z=3*x+4*y;
x=0,1,2,...,7; y=-3,-1,1,....,15.
Печать функции оформить в виде таблицы с заголовком:
x y z f(z)
Задача 2 (вариант 27)
Дана матрица:
Заменить отрицательные элементы матрицы нулями. Напечатать матрицу A с замененными элементами.
Задача 3 (вариант 27)
Дана матрица :
Вычислить и напечатать значение переменной T=S1-S2, где S1- сумма положительных элементов матрицы ; S2- произведение элементов, удовлетворяющих условию: a[i,j]<5.2.
Задача 4 (вариант 27)
Дана матрица:
Переменной L присвоить значение 1, если число положительных элементов над главной диагональю больше числа положительных элементов под главной диагональю и значение 0 в противном случае.
Задача 5 (вариант 27)
Дана матрица:
Преобразовать матрицу A, разделив все ее элементы на минимальный элемент. Вывести на печать преобразованную матрицу и минимальный элемент матрицы A.
Задача 6 (вариант 27)
Элементы матрицы A(5,3) определяются по формуле:
a[i,j]=Ln(2i+j).
Вычислить элементы массива X по формуле:
x[j]=Sin(j) + S[j] , где j=1,2,3;
S[j] - сумма положительных элементов j-ого столбца матрицы A.
Задача 7 (вариант 27)
Дана матрица:
Переменной T присвоить значение равное скалярному произведению векторов X и Y, где компоненты вектора X определяются как минимальные элементы строк, а компоненты вектора Y - максимальные элементы столбцов матрицы A.
Задача 8 (вариант 27)
Дана матрица:
в которой только два одинаковых элемента. Найти эти элементы и напечатать их индексы.
Задача 1 (вариант 28)
Вычислить значения функции от двух переменных:
для 1<=x<=3.5; hx=0.5; 2<=y<=4; hy=0.2.
Печать функции оформить в виде таблицы с заголовком:
x y z
Задача 2 (вариант 28)
Дана матрица:
Заменить элементы, расположенные выше главной диагонали, нулями. Напечатать исходную и полученную матрицы.
Задача 3 (вариант 28)
Дана матрица :
Найти произведение элементов матрицы, лежащих на главной диагонали и ниже ее.
Задача 4 (вариант 28)
Дана матрица:
Определить сумму и количество элементов матрицы, попадающих в интервал (-1,4).
Задача 5 (вариант 28)
Дана матрица:
Найти отношение максимального элемента к минимальному.
Задача 6 (вариант 28)
Дана матрица:
Вычислить произведение сумм квадратов элементов каждого столбца матрицы A.
Задача 7 (вариант 28)
Дана матрица:
Компоненты вектора X вычисляются по формуле:
,
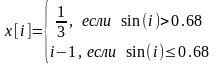где i=1,2,3.
Вычислить компоненты вектора Z, каждая из которых равна скалярному произведению строки матрицы A на вектор X.
Задача 8 (вариант 28)
Сформировать двумерный массив M(n,n) (где n - нечетное число) таким образом, чтобы "углы" и "центр" были заполнены нулями, а остальные элементы должны быть равны 1, т.е.
.
Задача 1 (вариант 29)
Вычислить значения функции:
f=G(x)+R(y), где
,
,
;
,
1<=y<=2;
dy=0.25.
Задача 2 (вариант 29)
Дана матрица:
Заменить отрицательные элементы матрицы на 1. На печать вывести исходную и полученную матрицы.
Задача 3 (вариант 29)
Дана матрица :
, и
Вычислить значение y=Cos(S1+S2) , где S1 - сумма положительных элементов матрицы A; S2 - произведение ненулевых элементов матрицы B.
Задача 4 (вариант 29)
Дана матрица:
Подсчитать количество элементов, абсолютная величина которых не превосходит число 5.
Задача 5 (вариант 29)
Дана матрица:
Вычислить величину L=Max-│Min│, где Max - целая часть максимального элемента; Min - целая часть минимального элемента матрицы A.
Задача 6 (вариант 29)
Дана матрица:
Вычислить элементы массива Y по правилу:
y[i]=Cos(x[i]) , где