X[j] - сумма положительных элементов j-го столбца матрицы a.

Задача 7 (вариант 14)

Дана матрица:

Сформировать матрицу Sign, определяющую знаки чисел матрицы A, по следующему правилу:

.

Подсчитать в полученной матрице количество элементов, имеющих значение 1, количество элементов, имеющих значение -1, и количество нулевых элементов.

Задача 8 (вариант 14)

Сформировать двумерный массив M(n,n) (где n - нечетное число) таким образом, чтобы "углы" и "центр" были заполнены нулями, а остальные элементы должны быть равны 1, т.е.

.

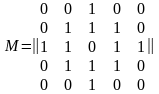Задача 1 (вариант 15)

Вычислить значения функции:

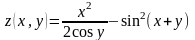, где , ;

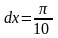y принимает 5 значений на интервале (1,2).

Печать z оформить в виде таблицы с заголовком:

x y z

Задача 2 (вариант 15)

Сформировать двумерный массив A, в котором элементы определяются по правилу:

a[i,j]=max[i+1,j] + Cos i , где i=1,2,...,m; j=1,2,...,n; m=3; n=4.

Задача 3 (вариант 15)

Дана матрица :

Вычислить и напечатать квадрат суммы положительных элементов и сумму квадратов отрицательных элементов матрицы.

Задача 4 (вариант 15)

Дана матрица:

В заданной матрице заменить все положительные элементы нулями, если количество отрицательных элементов больше, чем количество положительных элементов.

Задача 5 (вариант 15)

Дана матрица:

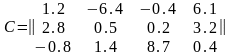
Среди элементов, расположенных в столбцах с нечетными номерами, найти максимальный элемент. На печать вывести найденный максимальный элемент и соответствующий ему номер столбца.

Задача 6 (вариант 15)

Дана матрица:

Сформировать массив C, в котором i-ый элемент равен разности между числом положительных и числом отрицательных элементов i-ой строки матрицы A.

Задача 7 (вариант 15)

Заданы вектор A(m), определяющий объем производимой функции, и матрица X(m,n), характеризующая распределение производимой продукции по N потребителям.

Требуется: 1. Вычислить невязки в векторе A как разность между компонентой a(i)

и суммой элементов 1-ой строки матрицы X.

2. Вычислить общую сумму невязок S в векторе A. Если S=0, т.е. вся

Продукция распределена, вывести на печать текст:

"ПЛАН ПЕРЕВОЗОК ОПТИМАЛЬНЫЙ"

При S<>0 напечатать значение S и текст:

"ПЛАН ПЕРЕВОЗОК НЕОПТИМАЛЬНЫЙ"

Исходные данные: m=3; m=4, A=(10,10,10);

.

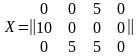Задача 8 (вариант 15)

Дана матрица:

Вычислить определитель матрицы.

Задача 1 (вариант 16)

Вычислить и напечатать в виде таблицы с заголовком значения функции:

,

Где значения x изменяются от 0 до 5 с шагом dx=0.5;

значения y изменяются от -2 до 1 с шагом dy=0.2.

Задача 2 (Вариант 16)

Дана матрица:

Вычислить матрицу B по формуле:

Задача 3 (вариант 16)

Дана матрица:

Вычислить сумму и произведение элементов матрицы, стоящих выше главной диагонали.

Задача 4 (вариант 16)

Дана матрица:

Найти количество отрицательных элементов, стоящих над главной диагональю.

Задача 5 (вариант 16)

Элементы матрицы A(10,10) вычисляются по формуле:

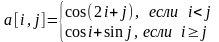
Найти минимальный элемент матрицы и его индексы. На печать вывести полученную матрицу и ее минимальный элемент вместе с индексами.

Задача 6 (вариант 16)

Дана матрица:

Найти максимальные элементы каждого столбца матрицы F и сумму всех положительных элементов.

Задача 7 (вариант 16)

Имеются экзаменационные ведомости студенческой группы из 21 человек по 5 дисциплинам. Определить средний бал по каждой дисциплине.

Задача 8 (вариант 16)

Даны матрицы:

Найти произведение матриц: C=A*B.

Задача 1 (вариант 17)

Вычислить значения функции:

,

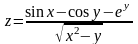Где значения x заданы массивом X=(-4,5,-2,1);

значения y изменяются на интервале [2,5] с шагом 0.6.

Печать оформить в виде таблицы с заголовком:

x y z

Задача 2 (Вариант 17)

Сформировать матрицу A по следующему правилу:

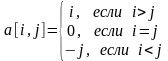, где

i=1,2,...,n; j=1,2,...,m; n=4; m=3.

Задача 3 (вариант 17)

Даны матрицы:

и

Найти сумму положительных и сумму отрицательных элементов матрицы C , в которой элементы вычисляются по формуле:

c[i,j]=2*a[i,j] + 3*b[i,j].

Задача 4 (вариант 17)

Дана матрица :

Вычислить сумму неотрицательных элементов и количество отрицательных элементов.

Задача 5 (вариант 17)

Дана матрица:

Найти минимальный элемент, расположенный на главной диагонали и номер столбца, в котором он находится.

Задача 6 (вариант 17)

Дана матрица:

Вычислить матрицу Z по правилу:

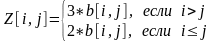
Найти вектор, состоящий из сумм элементов каждой строки матрицы Z, и минимальный элемент этого вектора.

Задача 7 (вариант 17)

Имеются экзаменационные ведомости студенческой группы из 21 человек по 5 дисциплинам. Определить количество пятерок, четверок, троек и двоек по каждой дисциплине

Задача 8 (вариант 17)

Переформировать двумерный массив:

в одномерный: (2, 7, -1, 0, 4, 5, 7, -5, 6).

Задача 1 (вариант 18)

Вычислить таблицу значений функции:

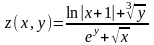, где , , .

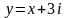Печать организовать так, чтобы три числа x,y,z

располагались в одной строке и каждая строка на печати

имела свой порядковый номер i:

i x y z

Задача 2 (Вариант 18)

Даны массивы:

A=(1,3,4,5,0,-2,1,0,9)

B=(3,2,4,1)

Вычислить и напечатать двумерный массив C,

элементы которого вычисляются по формуле:

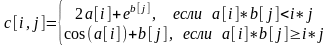
Задача 3 (вариант 18)

Дана матрица:

Вычислить произведение всех элементов матрицы, удовлетворяющих условию: C<=a[i,j]<=D, где C=-2.5; D=3.5.

Задача 4 (вариант 18)

Дана матрица:

Вычислить произведение и количество отрицательных элементов матрицы.

Задача 5 (вариант 18)

Дана матрица:

Поменять местами наибольший и наименьший элементы матрицы. На печать вывести полученную матрицу.

Задача 6 (вариант 18)

Дана матрица:

Найти количество отрицательных элементов в каждой строке матрицы B.

Задача 7 (вариант 18)

Имеются экзаменационные ведомости студенческой группы из 21 человек по 5 дисциплинам. Определить в % качественную и абсолютную успеваемость по формулам:

, , где n - число студентов в группе; L3,L4,L5 - количество троек, четверок и пятерок по всем дисциплинам.

Задача 8 (вариант 18)

Дана матрица:

Переформировать ее таким образом, чтобы элементы каждой строки располагались в порядке возрастания.

Задача 1 (вариант 19)

Вычислить и напечатать значения функции:

, где