Колебательный переходный процесс.

В лабораторной работе параметры rLC-элементов подобраны та-ким образом, что сопротивление цепи меньше критического r < Rкр, а колебательный процесс возникает именно при замыкании ключа ЭК. Этому случаю соответствуют комплексно-сопряжённые корни характеристического уравнения цепи, а сам процесс характеризуется:

р_1,2 = - δ ± јω₀ = ± j 1/с.

ω₀ = – частотой свободных колебаний, рад/с;

δ = = – коэффициентом затухания этих колебаний, 1/с.

Ток заряда и напряжение на конденсаторе совершают затухающие колебания вокруг своих установившихся значений:

u_С(t) = U₀ - , (11.2)

i (t) = , . (11.3)

Максимальное значение напряжения на конденсаторе u_{С макс}(t) стремится к значению 2U₀, а тока i_{С макс}(t) - к U₀ / ω₀L.

Г рафики тока и напряжения при колебательном процессе (левая часть рис. 11.2-11.3) построены для цепи с параметрами:

U₀ = 5B, R₁ =75 Ом, R₂ = 510 Ом, L = 100 мГн, С = 2 мкФ.

Рис. 11.2. График напряжения на конденсаторе при заряде (колебательный

характер) и при разряде (апериодический характер переходного процесса)

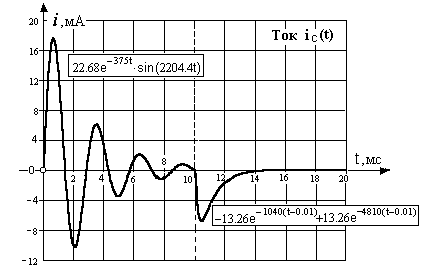
Рис.11.3. График тока конденсатора при заряде (колебательный характер

процесса) и при разряде (апериодический характер)

Характеристики колебательного процесса δ и ωсв можно определить по осциллограмме определить по выражениям:

, рад/с ; δ = , 1/с

Максимальное значение напряжения на конденсаторе u_{С макс}(t) стремится к значению 2U₀, а тока - к U₀ / ω₀L.

Апериодический процесс в rLC-цепи имеет место при r > Rкр, в лаборатории он наблюдается при размыкании ключа ЭК. Характе-ристическое уравнение имеет два разных вещественных корня р₁ и р₂. Поэтому такой переходный процесс характеризуют двумя посто-янными времени: τ₁ и τ₂. Хотя в целом процесс и апериодический, но идёт в два темпа, сначала быстрее, а затем медленнее. Этим он существенно отличается от апериодического процесса в цепях с од-ним накопителем энергии.

u_С(t) = ; (11.4)

i (t) = ; (11.5)

Графики изменения тока i(t) и напряжения u_С(t) при апериоди-ческом процессе представлены на рис.11.2-11.3 – правая половина рисунков. Напряжение на конденсаторе с течением времени плав-но уменьшается от начального значения u_C(0)= U₀ до нуля. Ток при разряде конденсатора меняет направление и сначала возрастает по абсолютной величине, а затем уменьшается до нуля при полном раз-ряде конденсатора.

Практическая продолжительность переходного процесса в основ-ном определяется большей постоянной времени цепи τ₁. Её достаточно достоверно можно определить и по осциллограммам. Для этого так же следует выделить и рассмотреть свободную составляю-шую тока или напряжения, воспользовавшись соотношением:

iсв (t₁+τ₁) = = 0.368 iсв (t₁).