Добавил:

Studfiles Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

Физика

Файл:

Dz_reshenie

.pdf

Скачиваний:

462

Добавлен:

25.04.2014

Размер:

560.14 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Рисунок 20

Коэффициент прохождения частицы через потенциальный барьер определяется выражением:

æ		2 x2		ö
æ		2 x2		ö
ç		ò		÷
D » expç	-		2m (U (x) - E)dx ÷		(1)
è		h x1	0	ø
è		h x1		ø
где пределы интегрирования x1				и x2	являются решениями уравнения:
U (x) = E					(2)

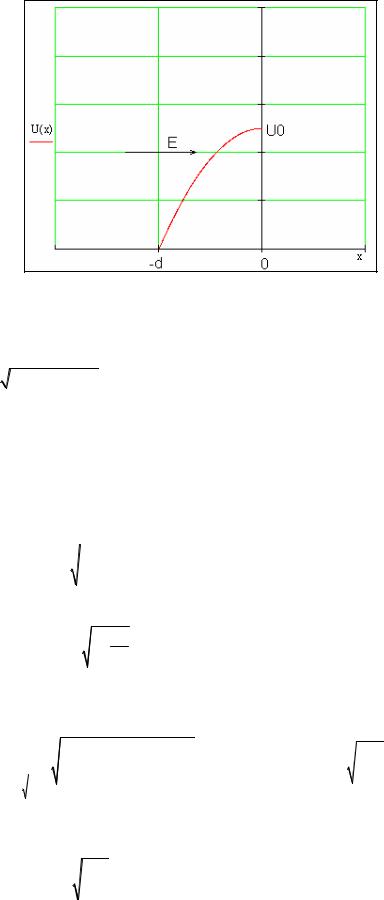
В нашем случае верхний предел интегрирования x2 = 0 , а нижний найдём из уравнения:

	æ	2		ö			E
U0	ç1	-	x1	÷	= E Þ x1	= ±d 1-
			2				U0
	è		d	ø

Берём отрицательный корень, так как положительный не принадлежит интервалу

−d < x < 0 . Значит, x1 = -d 1- E . Подставим в выражение (1) вид потенциальной

энергии в нашем случае и пределы интегрирования найдём коэффициент прохождения частицы через потенциальный барьер в зависимости от энергии частицы E :

æ		2
ç		2		0
D(E) » expç	-				ò
D(E) » expç	-	h
ç
ç						E
ç			−d		1−
è						U0

Ответ:

x2 ö

π d(U

- E)

çU

- E ÷dx ÷

= expç

(3)

2U0 ø

æ		π d(U		- E)			ö
					m
D(E) » expç	-		0		0	÷ .

ç		h			2U0	÷
è						ø

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Задача № 37.

Считая, что радиоактивный α -распад происходит за счёт туннелирования α -частицы через потенциальный барьер, получите закон радиоактивного α -распада, определяющий зависимость числа нераспавшихся ядер от времени распада t . Скорость α -частицы в материнском ядре равна v , радиус ядра - r0 , коэффициент прозрачности потенциального

барьера - D , число нераспавшихся ядер в начальный момент времени - N0 .

Решение:

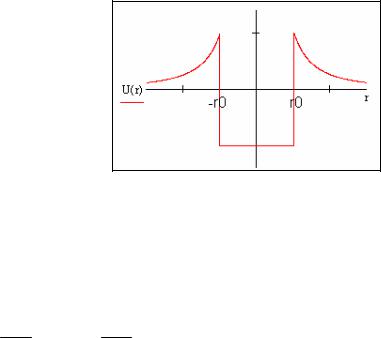
Вид потенциального барьера, который преодолевает α -частица при радиоактивном α - распаде представлен на рисунке 1:

Рисунок 21

На расстояниях порядка ядерного ядра действуют ядерное силы, конкретный вид которых до конца не известен, поэтому будем предполагать, что на интервале −r0 < r < r0 график потенциальной энергии имеет вид потенциальной ямы. Как увидим далее, это предположение на решение не влияет. На расстояниях больше порядка r0 ядерные силы уже не действуют, но действую кулоновские силы притяжения α -частицы и ядра:

U (r) = 2Zer 2 k , где k = 4πε1 0 .

Предположим, что радиоактивный α -распад происходит за счёт туннелирования α - частицы через потенциальный барьер из области ядра. Если коэффициент прозрачности потенциального барьера равен D , значит, из N нераспавшихся ядер в некоторый момент времени за время τ0 распадётся DN ядер. Время τ0 определяет время, которое

необходимо α -частицы, чтобы покинуть материнское ядро. Оно равно:

τ0 =	2r0	(1)
	v

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Возьмём достаточно малый промежуток времени dt , за который число нераспавшихся

ядер можно считать постоянным. Тогда за время dt происходит				dt тактов деления, при
этом число нераспавшихся ядер уменьшается на:				τ0
этом число нераспавшихся ядер уменьшается на:
dN = -DN dt		= - Dv Ndt	(2)
τ	0	2r
	0	0

Знак минус показывает уменьшение числа нераспавшихся ядер. Приведём выражение (2) к виду, удобному для интегрирования:

dN	= - Dv dt	(3)
N	2r
	0

Проинтегрировав обе части, получим:

æ		ö
N(t) = C expç	-	Dv	t ÷	(4)

è		2r0 ø

где C - некоторая постоянная, которую определим, используя начальные условия:

N(0) = C = N0

(5)

Таким образом, мы пришли к закону радиоактивного распада:

	æ		ö
N(t) = N0	expç	-	Dv	t ÷	(6)

	è		2r0 ø

Как известно, закон радиоактивного распада имеет вид:

N(t) = N0 exp(-λt)

(7)

В нашем случае, предполагая, что радиактивный α -распад происходит за счёт туннелирования α -частицы через потенциальный барьер, для постоянной распада мы получили следующее выражение:

λ =	Dv	(8)
	2r
	0

Ответ:

N(t) = N0 exp(-λt)

λ= Dv . 2r0

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Задача № 38.

Частица массой m0 падает на прямоугольный потенциальный порог высотой U0 . Энергия частицы равна E , причём E < U0 . Найдите эффективную глубину проникновения

частицы в область порога, то есть на расстоянии от границы порога до точки, в которой плотность вероятности нахождения частицы уменьшается в e раз.

Решение:

На рисунке 1 показан вид потенциального порога:

ì0, x < 0

U (x) = í

îU0 , x > 0

Рисунок 1

Составим уравнение Шредингера для областей 1 и 2:

Для области 1:

¶2ψ1

2m0

Eψ

= 0

(1)

¶x2

Для области 2:

¶2ψ 2

2m0

(E -U

)ψ

= 0

(2)

¶x2

Или в виде:

¶2ψ1

+ k

2ψ

= 0

(3)

¶x2

¶2ψ 2

+ k 2ψ

= 0

(4)

¶x2

где k2 =

2m0

E и

2m0

(E -U

)

. Заметим, что, так как мы рассматриваем случай, когда

E < U0 , то k2

будет чисто мнимым. Решения дифференциальных уравнений (3) и (4)

имеют вид:

ψ1(x) = A1 exp(ik1x) + B1 exp(-ik1x)

(5)

ψ 2 (x) = A2 exp(ik2 x) + B2 exp(-ik2 x)

(6)

Первое слагаемое выражения (5) соответствует падающей волне де Бройля частицы, второе слагаемое – отражённой волне. Первое слагаемое выражения (6) соответствует

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

прошедшей дебройлевской волне частицы, других волн во второй области нет, поэтому B2 = 0 . Тогда выражение (6) примет вид:

ψ 2 (x) = A2 exp(ik2 x)

(7)

Используем естественные условия, накладываемые на пси-функцию. Из условия непрерывности пси-функций, имеем для точки x = 0 :

ψ1(0) =ψ 2 (0) Þ A1 + B1 = A2

Используя условие гладкости пси-функций в точке

ψ1 '(0) =ψ 2 '(0) Þ k1 A1 - k1B1 = k2 A2

Из уравнений (8) и (9) найдём:

B1	=		k1 − k2
A			k + k				2
1			1				2
A2		=			2k1
A				k		+ k		2
1			1					2

(8)

x = 0 , получим:

(9)

(10)

(11)

Рассмотрим поток плотности вероятности. Он определяется также как и поток других

физических величин: Ф : vA2 , где v - скорость частицы, а A2 - квадрат амплитуды пси- функции, который определяет плотность вероятности нахождения частицы. Учитывая, что v : p : k , получим:

Ф : kA2

(12)

В нашем случае, для падающей, отражённой и прошедшей волн потоки плотности вероятности:

Для падающей волны:	Ф : k1 A12	(13)
Для отражённой волны:	Ф ' : k1B12	(14)
Для прошедшей волны:	Ф '' : k2 A22	(15)

Тогда мы можем найти коэффициенты отражения и пропускания:

	R =	Ф '		k B2			k - k	2	2

Коэффициент отражения:			=	1	1	=	1		(16)
		Ф		k A2			k + k	2

				1	1		1
Учитывая, что при E < U0	k2 чисто мнимое, имеем R = 1. Тогда коэффициент пропускания

равен нулю. Но это не значит, что частица не может находиться в области 2. Поведение частицы в области 2 описывается пси-функцией (7), тогда плотность вероятности нахождения частицы равна:

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

ρ(x) =	ψ 2	2 = ρ(0)exp(2ik2 x) = ρ(0)exp(-2κ x)					(17)
ρ(x) =	ψ 2	2 = ρ(0)exp(2ik2 x) = ρ(0)exp(-2κ x)					(17)

Мы сделали замену κ = ik2			=	2m0 (U0	- E)	. Пусть l	- эффективная глубина
Мы сделали замену κ = ik2			=	h		. Пусть l	- эффективная глубина
				h

проникновения частицы в область потенциального порога, то есть такое расстояние от границы порога, на котором плотность вероятности нахождения частицы уменьшается в e раз. Тогда:

ρ(l) =

ρ(0)

= ρ(0)exp(-2κl) Þ -2κl = -1Þ l =

(18)

2κ

Учитывая, что κ =

2m0 (U0

- E)

, получим для эффективной глубины проникновения

частицы в область потенциального порога выражение:

l =

(19)

2m (U

- E)

8m (U

- E)

Ответ:

l =

8m (U

- E)

Задача № 39.

Частица с энергией E падает на прямоугольный потенциальный порог высотой U0 .

Найдите приближённое выражение для коэффициента отражения R для случая UE0 =1.

Решение:

Вид потенциального порога представлен на рисунке 1:

Рисунок 22

Составим уравнения Шредингера для областей 1 и 2:

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Для области 1:

¶2ψ1

Eψ

= 0

(1)

¶x2

Для области 2:

¶2ψ 2

(E -U

)ψ

= 0

(2)

¶x2

Или в виде:

Для области 1:

¶2ψ1

+ k2ψ

= 0 , где

(3)

¶x2

Для области 2:

¶2ψ 2

+ k 2ψ

= 0 , где k2

(E -U

)

(4)

¶x2

Решения дифференциальных уравнений (3) и (4) имеют вид:

ψ1(x) = A1 exp(ik1x) + B1 exp(-ik1x)

(5)

ψ 2 (x) = A2 exp(ik2 x) + B2 exp(-ik2 x)

(6)

В выражении (5) первое слагаемое является уравнением падающей волны де Бройля электрона, а второе слагаемое – уравнение отражённой волны. В области 2 есть только прошедшая волна, которой соответствует первое слагаемое уравнения (6), поэтому коэффициент B2 = 0 . Уравнение (6) примет вид:

ψ 2 (x) = A2 exp(ik2 x)

(7)

Используя условие непрерывности пси-функций, для точки x = 0 запишем:

ψ1(0) =ψ 2 (0) Þ A1 + B1 = A2

(8)

Используя условие гладкости пси-функций, для точки x = 0 можем записать:

ψ1 '(0) =ψ 2 '(0) Þ k1 A1 - k1B1 = k2 A2										(9)
Используя уравнения (8) и (9), найдём:
	B1	=		k1 − k2						(10)
	A
				k + k				2
1				1
	A2		=			2k1				(11)
	A				k				2
							+ k
1				1

Рассмотрим поток плотности вероятности, который определяется также как и поток

любой другой физической величины: P : vA2 , где v - скорость частицы, а A2 - квадрат амплитуды волновой функции, характеризующий плотность вероятности местонахождения частицы. Так как скорость частицы v : p : k , то для падающей,

отражённой и прошедшей волн де Бройля электрона в нашем случае можно записать:

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Для падающей волны:

P : k1 A12

(12)

Для отражённой волны:

P ' : k1B12

(13)

Для прошедшей волны:

P '' : k2 A22

(14)

Теперь определим коэффициенты, учитывая также выражения (10) и (11):

P '

- k2

ö2

Коэффициент отражения:

R =

k1B1

= ç

(15)

P k1 A1

è k1 + k2 ø

Коэффициент пропускания:

D =

P ''

4k k

(16)

k A2

+ k

Сумма коэффициентов отражения и пропускания (коэффициента прозрачности

потенциального порога) равна 1:

R + D = 1

(17)

Учитывая, что k =

2m0 E

и k =

2m0 (E -U0 )

для коэффициента отражения получим:

ö2

- 1-

æ k - k

ö2

E -U

R = ç

= ç

(18)

k + k

2 ø

E + E -U

+ 1-

E ø

Учитывая условие UE0 =1, получим: R ≈ 0 , то есть при UE0 =1 отражённая дебройлевская волна практически отсутствует.

Ответ:

ö2

R = ç

» 0 .

Задача № 41.

Определите возможные результаты измерений квадрата модуля момента импульса L2 для частицы, находящейся в состоянии, описываемой волновой функцией

ψ (θ,ϕ) = Asinθ cosϕ , где θ - полярный угол, ϕ - азимутальный угол, A - некоторая нормировочная постоянная.

Решение:

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Если в некотором состоянии некоторая физическая величина принимает точно определённые значения, то такие значения называются собственными значениями этой физической величины, а пси-функции, которые описывают такие собственные состояния, являются решениями операторного уравнения:

	(1)
Qψ = Qψ

где Q - оператор некоторой физической величины Q , а в правой части уравнения Q -

собственное значение этой физической величины. В нашем случае необходимо найти собственные значения квадрата модуля момента импульса, поэтому уравнение (1) в данном случае имеет вид:

	(2)
L2 ψ = L2ψ

где L2 - оператор квадрата модуля момента импульса, который в сферических координатах имеет вид:

2 æ

1 ¶ æ

¶ ö

1 ¶

çsinθ

L = -h ç

÷ +

(3)

sin

θ ¶ϕ

è sinθ ¶θ è

¶θ ø

Подставим в операторное уравнение (2) вид оператора и пси-функцию и после преобразований получим:

2h2 Asinθ cosϕ = L2 Asin cosϕ Þ L2 = 2h2

(4)

Таким образом, собственное значение квадрата момента импульса в данном состоянии равняется L2 = 2h2 .

Ответ:

L2 = 2h2 .

Задача № 42.

Определите возможные результаты измерений проекции момента импульса Lz на

выделенное направление для частицы, находящейся в состоянии, описываемом волновой функцией ψ (θ,ϕ) = Asinθ cosϕ , где θ - полярный угол, ϕ - азимутальный угол, A - некоторая нормировочная постоянная.

Решение:

Если некоторая физическая величина имеет точно определённые значения в некотором состоянии, то такое состояние называется собственным. Пси-функции собственных состояний являются решением операторного уравнения:

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

	(1)
Qψ = Qψ

где Q - оператор физической величины Q , в правой части Q - собственное значение этой физической величины. В нашей задаче необходимо определить собственные значения проекции момента импульса Lz , поэтому операторное уравнение (1) в нашем случае имеет вид:

	ψ = Lzψ
Lz	ψ = Lzψ		(2)

где Lz		- оператор проекции момента импульса на ось z , который в сферических
координатах имеет вид:
	= h	¶
L		¶	(3)
L		¶ϕ	(3)
z	i
	i

Найдём собственные пси-функции, соответствующие состояниям, в которых проекция момента импульса на ось имеет определённые значения. Для этого решим операторное уравнение:

L ψ = L ψ Þ h ¶ψ			= L ψ	(4)

z	z	i ¶ϕ	z
		i ¶ϕ
Решая дифференциальное уравнение (4), получим:
ψ m = C exp(imϕ )				(5)

где m =

, m = 0, ±1, ±2,... C - постоянная, которую найдём из условия нормировки:

2òπ

ψ m

2dϕ =1Þ C2

2òπ

exp(imϕ)

2 dϕ =1Þ C =

(6)

2π

В этом случае собственные пси-функции имеют вид:

ψ m =

exp(imϕ )

(7)

2π

Определим постоянную A в выражении для пси-функции данного состояния, используя условие нормировки:

π	2òπ			π	2òπ sin2 θ cos2 ϕdθdϕ =1Þ A =
ò2		ψ	2dθdϕ = 1Þ A2	ò2			2	(8)
							2
						π
−π	0			−π	0	π
−π	0			−π	0
2				2

Тогда пси-функция данного состояния имеет вид:

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в папке Dz_1

#
25.04.2014560.14 Кб462Dz_reshenie.pdf
#
25.04.2014311.52 Кб166Dz_uslovie.pdf