

где vв , vc - фазовые скорости дебройлевской волны в вакууме и среде соответственно.
Учитывая, что фазовая скорость равна vф = ωk , а k = 2λπ , где λ - дебройлевская длина волны, получим:
n = |
vв |
= |
kc |
= λв |
(2) |
|
|
||||
e |
vc |
|
kв |
λc |
|
|
|
|
По определению длина волны де Бройля:
λ = |
2π h |
(3) |
Б p
где p – импульс электрона.
В вакууме кинетическая энергия электрона была равна K1 = eU , его импульс:
p1 = |
2mK1 |
= |
2meU |
(4) |
Дебройлевская длина волны электрона в вакууме:
λв = |
|
2π h |
|
(5) |
|
|
|
|
|||
2meU |
|||||
|
|
|
|
В кристалле энергия электрона увеличится на величину eϕ . На рисунке 1 представлены графики зависимости ϕ(x) и U (x) = −eϕ(x) . Из рисунка справа ясно, что
K2 = K1 + eϕ = e(U +ϕ) . Тогда длина волны де Бройля электрона в кристалле:
λc = |
|
2π h |
|
|
|
(6) |
|
|
|
|
|
||
2me(U |
|
|
||||
|
|
+ϕ) |
||||
|
|
|
|
|
|
|
Рисунок 4
Используя (2), найдём показатель преломления:
n = λв |
= |
|
U +ϕ |
|
= |
1+ ϕ |
(7) |
|
|
||||||||
e |
λc |
|
|
U |
U |
|
||
|
|
|
|
|||||
Из соотношения (7) определим внутренний потенциал кристалла:
11
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

ϕ = U (n2 |
-1) |
(8) |
e |
|
|
Воспользуемся условием Вульфа-Брэггов для того, чтобы определить показатель преломления ne :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2d |
|
n2 |
- cos2 θ = kλ |
|
|
|
(9) |
|
|
|
|
|
|
||||||||||
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возведём обе части в квадрат и найдём n2 : |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
4d |
2 (n2 |
- cos2 θ ) = k2λ2 = k2 |
4π 2h2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
e |
|
|
|
|
|
|
|
|
в |
|
|
2meU |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n2 |
= k2 |
|
|
π 2h2 |
|
+ cos2 θ |
|
|
|
|
|
|
(10) |
|
|
|
|
||||||
|
2meUd 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подставим полученное значение в уравнение (8): |
|
|
|
||||||||||||||||||||
|
æ |
|
|
2 π 2h2 |
|
|
|
2 |
|
ö |
æ |
2 |
π 2h2 |
|
|
2 |
ö |
|
|||||
ϕ = U ç k |
|
|
|
|
|
|
+ cos |
|
θ -1÷ |
= U çk |
|
|
|
- sin |
|
θ ÷ |
(11) |
||||||
|
2meUd |
2 |
|
|
2meUd |
2 |
|
||||||||||||||||
|
è |
|
|
|
|
|
|
|
ø |
è |
|
|
|
|
ø |
|
|||||||
Подставляя числовые значения, получим:
ϕ = 14.9В
Ответ:
æ |
2 |
π 2h2 |
|
|
2 |
ö |
ϕ = U ç k |
|
|
|
- sin |
|
θ ÷ |
|
2meUd |
2 |
|
|||
è |
|
|
|
|
ø |
ϕ = 14.9В
Задача № 7.
Коллимированный пучок электронов, прошедших ускоряющую разность потенциалов U = 30кВ , падает нормально на тонкую поликристаллическую фольгу золота. На фотопластинке, расположенной за фольгой на расстоянии l = 20см от неё, получена
дифракционная картина, состоящая из ряда концентрических окружностей. Радиус первой окружности r = 3.4мм . Определите: а) брэгговский угол θБ , соответствующий первой
окружности; б) длину волны де Бройля электронов λ ; в) постоянную d кристаллической решётки золота.
Решение:
12
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Рисунок 2
|
|
Рисунок 1 |
|
||
Используя рисунок 2, определим угол α : |
|
||||
|
r |
æ r ö |
|
||
tgα = |
|
Þ α = arctg ç |
|
÷ |
(1) |
l |
|
||||
|
è l ø |
|
|||
Как видно из рисунка 1, угол α = 2×θБ , где θБ - брэгговский угол скольжения. Таким образом, мы можем найти брэгговский угол, соответствующий первой окружности:
θБ |
|
1 |
|
æ r ö |
= 8.5×10−3 |
|
(2) |
|||
= |
|
|
arctg ç |
|
÷ |
рад = 29' |
||||
2 |
|
|||||||||
|
|
|
è l ø |
|
|
|
||||
Длина волны де Бройля падающих на золотую фольгу электронов: |
|
|||||||||
λ |
= |
2π h |
|
|
|
|
|
(3) |
||
|
|
|
|
|
|
|||||
Б |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где p - импульс электронов. Считая электроны релятивистскими, определим их импульс:
|
1 |
|
|
|
|
p = |
|
K (K + 2mc2 ) |
(4) |
||
c |
|||||
|
|
|
|
где K = eU - кинетическая энергия электрона, а m - масса покоя электрона. Тогда дебройлевская длина волны электронов равняется:
λ = 2π hc = 6.98×10−12 м = 6.98пм (5)
Б
eU (eU + 2mc2 )
Воспользуемся условием Вульфа-Брэггов:
13
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

2d sinθБ = kλБ |
(6) |
где d - постоянная кристаллической решётки, k - порядок максимума (в нашем случае максимум первого порядка k = 1). Найдём из выражения (6) постоянную кристаллической решётки, учитывая, что значение θБ и λБ определяются соответственно выражениями (2)
и (5):
d = |
λБ |
|
= 4.1×10−10 м = 4.1нм |
(7) |
2sinθ |
|
|||
|
Б |
|
||
Ответ:
а) θБ = 29'
б) λБ = 6.98пм
в) d = 4.1нм .
Задача № 8.
Параллельный пучок электронов, ускоренный разностью потенциалов U = 25В , падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми l = 50мкм .
Определите расстояние между соседними максимумами интерференционной картины на экране, отстоящим от щелей на расстоянии L = 100см .
Решение:
Найдём длину волны де Бройля, соответствующую электрону:
λБ = |
2π h |
(1) |
|
p |
|||
|
|
где p = 
 2mK - импульс электрона, K = eU - его кинетическая энергия. Таким образом, длина волны де Бройля электрона:
2mK - импульс электрона, K = eU - его кинетическая энергия. Таким образом, длина волны де Бройля электрона:
λ = |
|
2π h |
(2) |
|
|
Б 
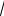 2meU
2meU
На рисунке 1 представлена схема установки:
14
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Рисунок 5
S1 и S2 –щели (вторичные источники). В результате интерференции волн от этих двух вторичных источников на экране появляется интерференционная картина. Из прямоугольных треугольников S1 AB и S2 AC по теореме Пифагора:
2 |
æ |
|
|
l |
ö2 |
2 |
|
|
|
|
|
|
(3) |
||
r1 |
= ç x - |
|
|
÷ |
+ L |
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|||||||||
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|||
2 |
æ |
|
|
l |
ö2 |
2 |
|
|
|
|
|
|
(4) |
||
r2 |
= ç x + |
|
|
|
÷ |
+ L |
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
||||||||
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|||
Вычтем из уравнения (4) уравнение (3): |
|
||||||||||||||
2 |
2 |
|
æ |
|
|
l ö2 |
2 |
æ |
l ö2 |
2 |
|
(5) |
|||
r2 |
- r1 |
= |
ç x + |
|
÷ |
+ L |
- ç x - |
|
÷ |
- L |
= 2xl |
||||
|
|
||||||||||||||
|
|
|
è |
|
|
2 ø |
|
è |
2 ø |
|
|
|
|||
Но, так как r2 |
- r2 |
= (r - r )(r |
+ r ) , где r |
- r - оптическая разность хода двух |
|||
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
интерферирующих волн |
|
, а r2 + r1 » 2L , так как r2 - r1 = L , то мы можем записать: |
|||||
2L ×D » 2xl |
|
|
|
|
|
|
(6) |
Если оптическая разность хода двух волн равна целому числу волн D = kλ , то образуется максимум. Используя уравнение (6) и условие максимумов, определим положение максимумов на экране xk :
x = kλL |
|
|
|
|
(7) |
|
k |
l |
|
|
|
|
|
|
|
|
|
|
|
|
Тогда расстояние между соседними максимумами: |
|
|||||
Dx = x |
k +1 |
- x = (k +1)λL |
- kλL = λL |
(8) |
||
|
k |
l |
l |
l |
|
|
|
|
|
|
|||
15
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Подставим в выражение (8) дебройлевскую длину волны электронов, падающих на диафрагму, получим:
Dx = |
|
2π hL |
|
(9) |
|
|
|
|
|
||
l |
|
2meU |
|||
|
|
|
|
||
Подставляя числовые значения, получим:
Dx = 4.9 ×10−7 м = 0.49мкм
Ответ:
x = 0.49мкм .
Задача № 9.
Узкий пучок электронов, прошедших ускоряющую разность потенциалов U = 50В , падает нормально на поверхность некоторого монокристалла. Определите, под каким углом к
нормали к поверхности кристалла наблюдается максимум отражения электронов первого порядка, если расстояние между отражающими атомными плоскостями кристалла составляет d = 0.2нм .
Решение:
Длина волны де Бройля электронов, прошедших ускоряющую разность потенциалов U :
λ |
= |
2π h |
= |
|
2π h |
= |
|
2π h |
|
(1) |
||
|
|
|
|
|
|
|
||||||
Б |
|
p |
|
|
|
2mK |
2meU |
|
||||
|
|
|
|
|
|
|||||||
где |
p = |
|
|
- импульс электрона, а K = eU - его кинетическая энергия. |
||||||||
|
2mK |
|||||||||||
Воспользуемся условием Вульфа-Брэггов: |
|
|||||||||||
2d sinθ = kλБ |
|
|
(2) |
|||||||||
где θ - угол скольжения (показан на рисунке 1), k |
- порядок максимума (в нашем случае |
|||||||||||
k = 1). Таким образом, учитывая выражение для дебройлевской длины волны электрона
(1), условие Вульфа-Брэггов в нашем случае примет вид: |
|
||||||
|
|
2π h |
æ |
|
π h ö |
|
|
2d sinθ = |
|
|
Þθ = arcsin ç |
|
|
÷ |
(3) |
|
|
|
|
||||
|
|
2meU |
è d |
2meU ø |
|
||
16
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

|
|
|
|
Рисунок 6 |
Из рисунка 1 видно, что: |
|
|||
α |
+θ = |
π |
Þ α = π - 2×θ |
(4) |
2 |
|
2 |
|
|
Учитывая выражение для угла скольжения θ , получим, что угол α , который необходимо найти, равен:
æ |
|
π h ö |
|
o |
|
|
α = π - 2×arcsin ç |
|
|
÷ |
= 2.69 рад = 128.57 |
|
(5) |
|
|
|
||||
è d |
2meU ø |
|
|
|
||
Ответ:
α =128.57o .
Задача № 10.
Нерелятивистская частица массой m1 , обладающая кинетической энергией Ek , налетает на покоящуюся частицу массой m2 . Найдите дебройлевские длины волн обеих частиц в системе их центра масс.
Решение:
Для начала определим скорость центра масс:
v = |
m1v1 + m2v2 |
= |
m1v1 |
|
(1) |
|
|
||||
c |
m1 + m2 |
|
m1 + m2 |
|
|
|
|
|
|||
так как в нашем случае v2 |
= 0 . Скорость первой частицы до соударения v1 найдём, |
||||
используя выражение для ёё кинетической энергии:
17
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

E |
|
= |
m v2 |
Þ v = |
|
2E |
|
(2) |
k |
1 1 |
k |
||||||
|
|
|||||||
|
|
2 |
1 |
|
m1 |
|
|
|
|
|
|
|
|
|
|
Найдём скорости частиц в системе их центра масс до соударения:
v1c = v1 |
- vc = v1 |
|
|
|
m1v1 |
= v1 |
æ |
|
|
m1 |
ö |
|
|
- |
|
ç1 |
- |
|
÷ |
|
|||||||
m1 + m2 |
m1 |
|
|
||||||||||
|
|
|
|
|
è |
|
+ m2 ø |
(3) |
|||||
|
|
|
|
m1v1 |
|
|
|
|
|
|
|
||
v2c = v2 |
- vc = - |
|
|
|
|
|
|
|
|
|
|||
|
m1 |
+ m2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
Пусть скорости частиц в системе их центра масс после соударения равны v1c ' и v2c '. Тогда
для системы центра масс запишем закон сохранения полной механической энергии и закон сохранения импульса (в системе центра масс сумма импульсов всех частиц, как известно, равна нулю):
|
m v2 |
+ |
|
m v2 |
= |
m (v |
')2 |
+ |
|
m (v |
')2 |
|
|
|
|
(4) |
|||||||||||
|
1 1c |
|
|
2 |
2c |
|
1 |
1c |
|
|
2 |
2c |
|
|
|
|
|
||||||||||
2 |
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
m1v1c '+ m2v2c ' = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|||||||||||||
Решая систему уравнений (4) и (5), получим: |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|||||||||||
v |
' = - |
|
|
|
|
|
|
|
|
× m m (m + m )(m v2 + m v2 |
) |
|
|||||||||||||||
|
m (m2 + m m ) |
||||||||||||||||||||||||||
|
1c |
|
|
|
|
|
|
|
|
1 2 |
1 |
2 |
1 1c |
2 2c |
|
|
|||||||||||
|
|
|
|
|
|
|
1 |
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
v |
' = |
|
|
|
|
|
|
|
|
× m m (m + m )(m v2 |
+ m v2 |
) |
|
|
|
||||||||||||
|
(m2 |
+ m m ) |
|
|
|||||||||||||||||||||||
|
2c |
|
|
|
|
|
1 2 |
1 |
|
2 1 1c |
2 2c |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С учётом выражений (3), получим:
(6)
(7)
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
æ |
|
|
æ |
|
|
m1 |
|
ö |
2 |
|
|
æ |
|
m1 |
|
|
|
ö |
2 |
ö |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
2 |
|
|
|
2 |
|
|
|
|
|
÷ |
|
|||||||||||||
v1c ' = - |
|
|
|
|
|
|
|
|
× |
m1m2 (m1 + m2 ) |
|
|
ç1 |
- |
|
|
|
÷ |
+ m2v1 |
ç |
|
|
|
|
|
|
÷ |
|
= |
|||||||||||||
|
|
|
2 |
+ m1m2 ) |
ç m1v1 |
m1 |
|
|
|
|
|
|
|
|
|
÷ |
||||||||||||||||||||||||||
|
|
|
|
|
m1(m2 |
|
|
|
|
|
è |
|
|
è |
|
+ m2 ø |
|
|
|
è m1 |
+ m2 ø |
|
ø |
|
||||||||||||||||||
|
|
m m2v |
|
= - (m2 |
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
- m (m2 + m m ) |
+ m m ) v1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
2 |
|
1 |
2 |
|
|
|
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
æ |
|
æ |
|
|
|
m1 |
|
ö |
2 |
|
|
æ |
|
m1 |
|
ö |
2 |
ö |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
2 |
|
|
|
|
|
2 |
|
|
÷ |
|
|
|
|
|
||||||||||||
v2c ' = |
|
|
2 |
+ m1m2 ) |
× m1m2 (m1 + m2 ) |
ç m1v1 |
ç1 |
- |
|
|
|
|
÷ |
+ m2v1 |
ç |
|
|
|
÷ |
|
÷ |
|
= |
|
|
|||||||||||||||||
|
|
|
(m2 |
|
|
|
|
|
|
è |
|
è |
|
|
m1 + m2 ø |
|
|
|
è m1 |
+ m2 ø |
|
ø |
|
|
|
|
|
|||||||||||||||
|
m1m2 |
|
|
v1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(m2 + m m ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(8)
(9)
Найдём импульсы этих частиц в системе центра масс:
18
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

|
|
|
|
|
|
|
|
|
m m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(10) |
||||
p1c ' = m1v1c ' = − (m2 + m m ) v1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
p2c ' = m2v2c |
' = |
|
m m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11) |
||||||||||
(m2 + m m ) v1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставляя сюда выражение для v1 |
из уравнения (2), получим: |
||||||||||||||||||||||||||||||
|
|
|
|
|
m m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
||||
|
|
' = − |
|
|
|
|
|
2E |
|
|
= − |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
p |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
2m E |
|
(12) |
||||||||||||||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
|
(m2 |
+ m m ) |
|
m |
|
|
(m2 |
+ m m ) |
|
||||||||||||||||||||||
1c |
|
|
|
|
|
|
|
|
1 |
k |
|
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
1 |
2 |
|
|
|
1 |
|
|
|
|
|
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
m m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
' = |
|
|
|
|
|
2E |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m E |
|
(13) |
|||||||||||||
|
|
|
|
1 2 |
|
|
|
|
|
k |
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
|
(m2 |
+ m m ) |
m |
|
(m2 |
+ m m ) |
|
||||||||||||||||||||||||
|
2c |
|
|
|
|
|
|
1 k |
|
|
|
||||||||||||||||||||
|
|
|
|
2 |
|
1 |
|
2 |
|
|
|
1 |
|
|
|
|
|
|
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
Найдём дебройлевские длины волн частиц в системе их центра масс:
|
|
|
2π h |
|
(m22 + m1m2 ) |
|
|
|
|
|
|
|
|
||||||
λ |
' = λ |
' = |
= π h |
|
|
|
|
2 |
|
(14) |
|||||||||
p |
|
' |
|
|
|
m E |
|
||||||||||||
1Бc |
2Бc |
|
2c |
|
|
m2 |
|
|
|
|
|
|
k |
||||||
|
|
|
|
|
|
|
2 |
|
1 |
||||||||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(m2 |
+ m m ) |
|
|
|
|
|
|
|
|
|
|
|||
λ |
' = λ |
' = π h |
2 |
|
|
. |
|
|
|
|
|
||||||||
|
2 |
|
1 2 |
|
|
|
|
|
|
|
|
||||||||
|
|
m2 |
m E |
|
|
|
|
|
|
||||||||||
1Бc |
2Бc |
|
|
|
|
|
k |
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
||||||
Задача № 11.
Считая, что минимальная энергия E нуклона (протона или нейтрона) в ядре равна 10МэВ, оцените, исходя из соотношения неопределённостей, линейные размеры ядра.
Решение:
Импульс нуклона в ядре равен: |
|
p =< p > +Δp |
(1) |
где < p > - среднее значение импульса нуклона, |
p - неопределённость импульса. Если |
среднее значение импульса равняется нулю < p >= 0 , то минимальное значение импульса
имеет порядок его неопределённости, то есть pmin = |
p . Отсюда следует, что минимальная |
|
энергия нуклона в ядре равняется: |
|
|
Emin = |
p2 |
(2) |
|
2m |
|
Из уравнения (2) найдём неопределённость импульса нуклона в ядре:
19
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Dp = |
2mEmin |
|
(3) |
|
где m =1.6×10−27 кг - масса нуклона. Воспользуемся первым соотношением |
||||
неопределённостей Гейзенберга: |
|
|
||
DpxDx : h |
(4) |
|||
В нашем случае неопределённость импульса Dp = |
|
, а Dx = lmin - минимальные |
||
2mEmin |
||||
линейные размеры ядра. Поэтому выражение (4) можно переписать в следующем виде:
|
×lmin : h |
(5) |
2mEmin |
Из выражения (5) можно оценить минимальные линейные размеры ядра lmin :
lmin : |
|
h |
|
=1.47 ×10−15 м |
(6) |
|
|
|
|||
2mE |
|||||
|
|
min |
|
|
|
Ответ:
lmin =1.47 ×10−15 м .
Задача № 12.
Кинетическая энергия электрона в атоме водорода составляет величину порядка 10эВ. Используя соотношение неопределённостей, оцените минимальные линейные размеры атома.
Решение:
Импульс электрона в атоме водорода равен:
p =< p > +Δp |
(1) |
где < p > - среднее значение импульса электрона в атоме водорода, а p -
неопределённость импульса. Из выражения (1) следует, что минимальное значение
импульса электрона в атоме водорода по порядку величины равняется его неопределённости pmin = Dp в случае, когда среднее значение импульса равняется нулю
< p >= 0 . В этом случае минимальная кинетическая энергия электрона Kmin определяется следующим образом:
Kmin = |
Dp2 |
(2) |
|
2m |
|||
|
|
Отсюда найдём неопределённость импульса:
20
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
