
3 семестp / Лекции / 2(Elektrostatika) / 05
.DOC1.9 Свойства равновесного распределения зарядов в проводнике.
![]() ,
так как
,
так как
![]() (то
есть постоянно), то получаем:
(то
есть постоянно), то получаем:
Свойство
№ 1:
в проводнике
![]() .
.
Свойство № 2: внутри проводника при равновесном распределении нет никаких электрических зарядов.
Р ассмотри
в объеме
ассмотри
в объеме
![]() теорему
Гаусса.
теорему
Гаусса.
![]() .
Так как
.
Так как
![]()
![]() .
.
Так как тело заряжено, следовательно, заряд равновесно распределен по его поверхности.
С войство
№ 3:
вектор напряженности электрического
поля заряженного проводника перпендикулярен
его поверхности.
войство
№ 3:
вектор напряженности электрического
поля заряженного проводника перпендикулярен
его поверхности.
![]() ,
где
,
где
![]() -вектор
внешней нормали. Так как
-вектор
внешней нормали. Так как
![]() ,
то
,
то
![]() (так
как
(так
как
![]() ),
но
),
но
![]() .
.
Пример:
![]()
 это
верно при
это
верно при
![]() .
.
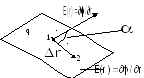
Эквипотенциальная поверхность – это поверхность, где работа по перемещению заряда равна нулю.
![]()
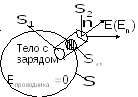 .
Пояснение:
.
Пояснение:
![]() так как
так как
![]() ,
,
![]() так как
так как
![]() .
.
![]() .
.
1.10 Сведения из векторного анализа.
Пусть
![]() –
скалярное поле, а
–
скалярное поле, а
![]() –
векторное поле, тогда
–
векторное поле, тогда
-
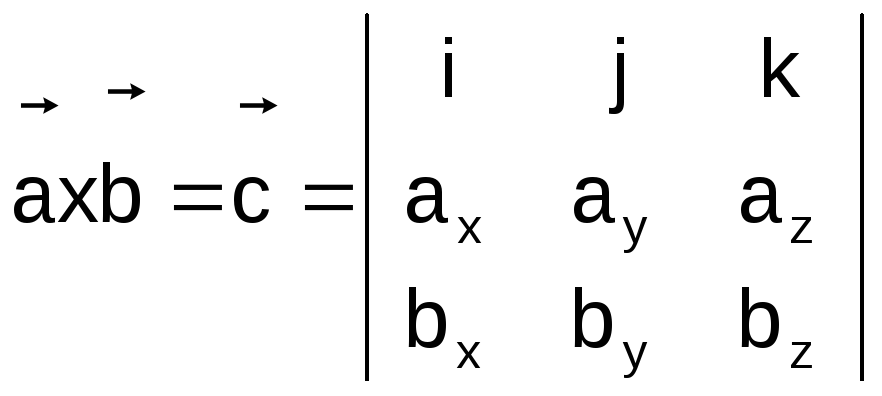 ;
;
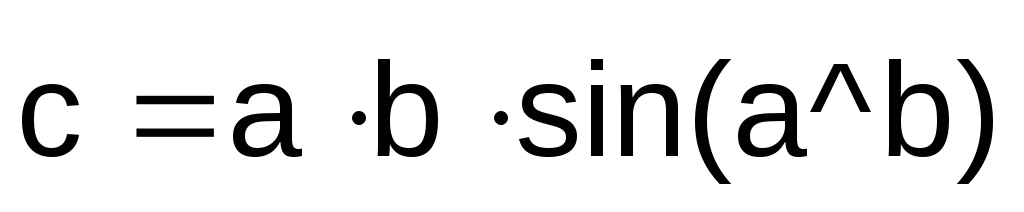 ;
;
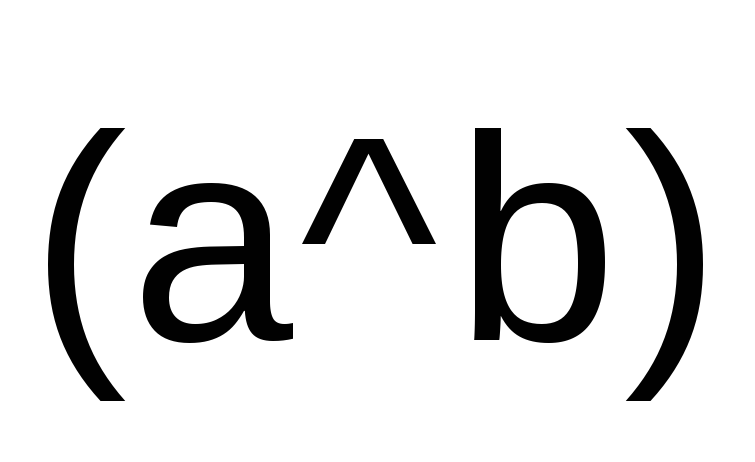 –
угол между векторами
–
угол между векторами
 и
и
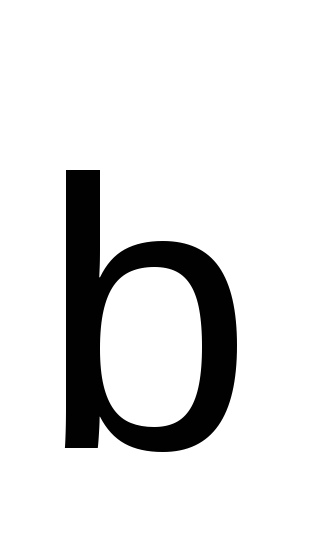 .
.
-
 ;
;
 – градиент
– градиент
-
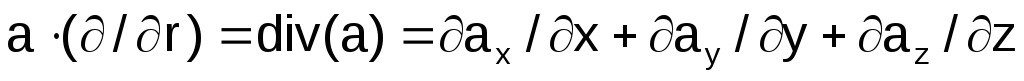 –дивергенция
–дивергенция
-
 – ротор
– ротор
Выражение для дивергенции в декартовой системе координат.
![]() .
.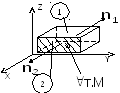 Поток через грань 2 равен
Поток через грань 2 равен
![]() .
Поток через грань 1 равен
.
Поток через грань 1 равен
![]() .
Поток через грани 1 и 2 вместе взятые
составляет соответственно
.
Поток через грани 1 и 2 вместе взятые
составляет соответственно
![]() .
Здесь
.
Здесь
![]() –
значение
–
значение
![]() ,
усредненное по грани 1, а
,
усредненное по грани 1, а
![]() –
значение
–
значение
![]() ,
усредненное по грани 2. Если устремить
,
усредненное по грани 2. Если устремить
![]() к нулю, то оно преобразуется в
к нулю, то оно преобразуется в
![]() ,
что в свою очередь равно
,
что в свою очередь равно
![]() .
Следовательно, окончательно получится
следующее:
.
Следовательно, окончательно получится
следующее:
![]() .
В данном выражении
.
В данном выражении
![]() берется в точке М. Аналогично рассуждая,
получаем, что
берется в точке М. Аналогично рассуждая,
получаем, что
![]() и
и
![]() .
Окончательно получаем
.
Окончательно получаем![]() .
Из этого следует, что
.
Из этого следует, что
![]()
![]() .
Легко видеть, что
.
Легко видеть, что
![]() – эта формула фактически является
формулировкой теоремы
Гаусса-Остроградского,
которую мы доказали прямо перед ней.
– эта формула фактически является
формулировкой теоремы
Гаусса-Остроградского,
которую мы доказали прямо перед ней.
Выражение для ротора в декартовой системе координат.
![]()
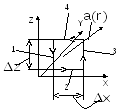 .
.
![]() – циркуляция вектора
– циркуляция вектора
![]() по
контуру с.
по
контуру с.
![]() –
произвольная поверхность, натянутая
на контур с. Найдем циркуляцию вектора
–
произвольная поверхность, натянутая
на контур с. Найдем циркуляцию вектора
![]() .
Для поиска циркуляции вводят нормаль
по правому винту.
. Минус перед ротором здесь потому что
. Совершенно аналогично мы получаем,
что и .
.
Для поиска циркуляции вводят нормаль
по правому винту.
. Минус перед ротором здесь потому что
. Совершенно аналогично мы получаем,
что и .
То, что мы сейчас делали является, фактически, доказательством теоремы Стокса: ᄃ
Замечания и примеры.
-
Так как ᄉ ᄃ и ᄉ ᄃследовательно получаем:ᄉ ᄃ–дифференциальная формулировка теоремы Гаусса.
-
ᄉ ᄃ, но ᄉ ᄃ, следовательно ᄉ ᄃ. Так как работа электрических сил по замкнутому контуру = 0, то ᄉ ᄃ и следовательно выражение ᄉ ᄃ является условием потенциальности электростатического поля.
