
- •Основні властивості (аксіоми) належності точок і прямих на площині
- •Висота, бісектриса, медіана трикутника
- •Дотична до кола
- •Геометричне місце точок
- •Пряма й обернена теореми
- •Доведеннявід супротивного
- •Приклади розв’язування типових задач з геометрії для 7 класу
- •Теорема Піфагора
- •Симетрія відносно прямої
- •Множення вектора на число
- •Скалярний добуток векторів
- •Подібність прямокутних трикутників
- •Пропорційність відрізків хорд і січних кола
- •Вписані й описані чотирикутники
- •Теорема синусів
- •Розв’язування трикутників
- •Многокутники
- •Правильні многокутники
- •Паралельність прямих і площини
- •Ознака паралельності площин
- •Перпендикулярність прямих і площин
- •Перпендикуляр і похила
- •Відстань між мимобіжними прямими
- •Кут між мимобіжними прямими
- •Декартові координати та вектори в просторі
- •Перетворення в просторі
- •Подібність просторових фігур
- •Вектори в просторі
- •Тригранний і многогранний кути
- •Паралелепіпед
- •Правильні многогранники
- •Описані кулі
Симетрія відносно прямої
Нехай
а
— фіксована пряма. Візьмемо довільну
точку Х
і опустимо перпендикуляр AX
на пряму а.
На продовженні цього перпендикуляра
за точку А
відкладемо відрізок
![]() .
Точка
називається
симетричною
точці X
відносно прямої а.
.
Точка
називається
симетричною
точці X
відносно прямої а.
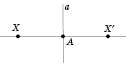 Якщо
точка X
лежить на прямій а,
то вона симетрична сама собі відносно
прямої а.
Очевидно,
що точка, симетрична точці
,
є точка X.
Перетворення
фігури F
у фігуру
Якщо
точка X
лежить на прямій а,
то вона симетрична сама собі відносно
прямої а.
Очевидно,
що точка, симетрична точці
,
є точка X.
Перетворення
фігури F
у фігуру
![]() ,
при якому кожна точка X
фігури F
переходить у точку
,
при якому кожна точка X
фігури F
переходить у точку
![]() ,
симетричну відносно даної прямої а,
називається перетворенням
симетрії відносно прямоїа.
Отримані фігури називаються симетричними
відносно прямоїа.
Якщо
перетворення симетрії відносно прямої
а
переводить фігуру F
у себе, то така фігура називається
симетричною
відносно прямоїа.
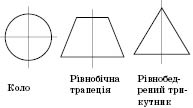
На
рисунках наведені приклади осей симетрії
фігур.
,
симетричну відносно даної прямої а,
називається перетворенням
симетрії відносно прямоїа.
Отримані фігури називаються симетричними
відносно прямоїа.
Якщо
перетворення симетрії відносно прямої
а
переводить фігуру F
у себе, то така фігура називається
симетричною
відносно прямоїа.
На
рисунках наведені приклади осей симетрії
фігур.

 Теорема.
Перетворення симетрії відносно прямої
є рухом.
Теорема.
Перетворення симетрії відносно прямої
є рухом.
Поворот
 Поворотом
площини навколо даної точки
називається такий рух, при якому кожний
промінь, що виходить із даної точки,
повертається на один і той самий кут в
одному й тому самому напрямку (див.
рисунок).
Поворотом
площини навколо даної точки
називається такий рух, при якому кожний
промінь, що виходить із даної точки,
повертається на один і той самий кут в
одному й тому самому напрямку (див.
рисунок).
Паралельне перенесення та його властивості
Перетворення
фігури F,
при
якому довільна її точка з координатами
переходить
у точку
![]() ,
де a
і b
— одні й ті самі для всіх точок, називається
паралельним
перенесенням.
Теорема.
Паралельне перенесення є рухом.
При
паралельному перенесенні пряма переходить
у паралельну пряму (або в себе) (див.
рисунок).
,
де a
і b
— одні й ті самі для всіх точок, називається
паралельним
перенесенням.
Теорема.
Паралельне перенесення є рухом.
При
паралельному перенесенні пряма переходить
у паралельну пряму (або в себе) (див.
рисунок).

Існування та єдиність паралельного перенесення
Теорема.
Які б не були дві точки А
і
![]() ,
існує одне, й тільки одне, паралельне
перенесення, при якому точка А
переходить у точку
.
,
існує одне, й тільки одне, паралельне
перенесення, при якому точка А
переходить у точку
.
Співнаправленість півпрямих
Дві
півпрямі називаються однаково
напрямленими
або співнапрямленими,
якщо вони суміщаються паралельним
перенесенням (рисунок 1).
Теорема.
Якщо півпрямі а
і b
однаково напрямлені й півпрямі b
і
c
однаково напрямлені, то півпрямі а
і c
також
однаково напрямлені.
Дві півпрямі
називаються протилежно
напрямленими,
якщо кожна з них однаково напрямлена
з півпрямою, доповняльною до другої
(рисунок 2).
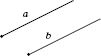 Рис.
1
a,
b
— співнапрямлені півпрямі
Рис.
1
a,
b
— співнапрямлені півпрямі
 Рис.
2
c,
d
— протилежно напрямлені півпрямі
Рис.
2
c,
d
— протилежно напрямлені півпрямі
Рівність фігур
Дві фігури називаються рівними, якщо вони переводяться рухом одна в одну. Теорема. Рівні трикутники (означення дивись у розділі «Геометрія. 7 клас») є рівними фігурами, тобто суміщаються рухом.
Вектори
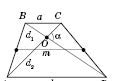
Вектором
називається напрямлений відрізок.
На
рисунку зображений вектор, який можна
позначити
![]() або
або
![]() .
.
![]() Вектори
і
Вектори
і
![]() називаються
однаково
напрямленими,
якщо однаково напрямлені півпрямі AB
і CD.
Вектори
і
називаються
протилежно
напрямленими,
якщо протилежно напрямлені півпрямі
AB
і CD.
Абсолютною
величиною,
або модулем
вектора,
називається довжина відрізка, що зображує
вектор.
Позначення:
називаються
однаково
напрямленими,
якщо однаково напрямлені півпрямі AB
і CD.
Вектори
і
називаються
протилежно
напрямленими,
якщо протилежно напрямлені півпрямі
AB
і CD.
Абсолютною
величиною,
або модулем
вектора,
називається довжина відрізка, що зображує
вектор.
Позначення:
![]() або
або
![]() .
Вектор
називається нульовим,
якщо початок вектора збігається з його
кінцем.
Позначення:
.
Вектор
називається нульовим,
якщо початок вектора збігається з його
кінцем.
Позначення:
![]() .
Нульовому
вектору не приписують ніякого напряму:
.
Нульовому
вектору не приписують ніякого напряму:
![]() .
Два
вектори називаються рівними,
якщо вони суміщаються паралельним
перенесенням.
Два вектори рівні
тоді й тільки тоді,
коли вони однаково напрямлені й рівні
за абсолютною величиною.
Два ненульові
вектори називаються колінеарними,
якщо вони лежать на одній прямий або на
паралельних прямих. Колінеарні вектори
або однаково напрямлені, або протилежно
напрямлені.
Позначення:
.
Два
вектори називаються рівними,
якщо вони суміщаються паралельним
перенесенням.
Два вектори рівні
тоді й тільки тоді,
коли вони однаково напрямлені й рівні
за абсолютною величиною.
Два ненульові
вектори називаються колінеарними,
якщо вони лежать на одній прямий або на
паралельних прямих. Колінеарні вектори
або однаково напрямлені, або протилежно
напрямлені.
Позначення:
![]() .
Теорема.
Нехай
.
Теорема.
Нехай
![]() —
вектор і A
— довільна точка. Тоді від точки А
можна відкласти один і тільки один
вектор
—
вектор і A
— довільна точка. Тоді від точки А
можна відкласти один і тільки один
вектор
![]() ,
що дорівнює вектору
,
що дорівнює вектору
![]() .
.
Координати векторa
Нехай
вектор
має
початком точку
![]() ,
а кінцем — точку
,
а кінцем — точку
![]() .
Координатами
вектора
називаються
числа
.
Координатами
вектора
називаються
числа
![]() і
і
![]() .
Позначення:
.
Позначення:
![]() або
або
![]() .
.
![]() .
Очевидно,
що
.
Очевидно,
що
![]() .
Теорема.
Вектори рівні тоді й тільки тоді,
коли вони мають рівні відповідні
координати.
.
Теорема.
Вектори рівні тоді й тільки тоді,
коли вони мають рівні відповідні
координати.
Додавання векторів
Сумою
векторів
і
![]() називається
вектор
називається
вектор
![]() .
Додавання
векторів має переставну та сполучну
властивості:
.
Додавання
векторів має переставну та сполучну
властивості:
![]() ;
;
![]() для
будь-яких
для
будь-яких
![]() ,
,
![]() ,
,
![]() .
Теорема.
Які б не були точки A,
B,
C,
справджується векторна рівність:
.
Теорема.
Які б не були точки A,
B,
C,
справджується векторна рівність:
![]() .
.
Правило трикутника додавання векторів
Щоб
знайти суму довільних векторів
і
![]() ,
треба від кінця вектора
(див.
рисунок) відкласти вектор
,
треба від кінця вектора
(див.
рисунок) відкласти вектор
![]() ,
що дорівнює вектору
.
Тоді вектор, початок якого збігається
з початком вектора
,
а кінець — з кінцем вектора
,
буде сумою векторів
і
.
,
що дорівнює вектору
.
Тоді вектор, початок якого збігається
з початком вектора
,
а кінець — з кінцем вектора
,
буде сумою векторів
і
.

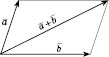
Правило паралелограма
Для
векторів із спільним початком їх сума
зображується діагоналлю паралелограма,
побудованого на цих векторах, яка
виходить з їх спільного початку (див.
рисунок).
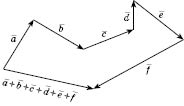
 Якщо
треба знайти суму кількох векторів,
можна скористатися правилом многокутника
(див. рисунок).
Якщо
треба знайти суму кількох векторів,
можна скористатися правилом многокутника
(див. рисунок).
 Різницею
векторів
Різницею
векторів![]() і
і
![]() називається
такий вектор
називається
такий вектор
![]() ,
який у сумі з вектором
дає
вектор
,
який у сумі з вектором
дає
вектор
![]() :
:
![]() .
Теорема.
Для векторів
і
.
Теорема.
Для векторів
і
![]() із
спільним початком
із
спільним початком
![]() .
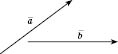
Щоб
знайти різницю векторів
і
,
треба від однієї точки відкласти вектори
в
.
Щоб
знайти різницю векторів
і
,
треба від однієї точки відкласти вектори
в
![]() і
,
що дорівнюють їм (див. рисунок). Тоді
вектор, початок якого збігається з
кінцем вектора
,
а кінець — з кінцем
,
буде різницею
і
.
і
,
що дорівнюють їм (див. рисунок). Тоді
вектор, початок якого збігається з
кінцем вектора
,
а кінець — з кінцем
,
буде різницею
і
.
 Тобто,
якщо вектори
Тобто,
якщо вектори
![]() і
мають
спільний початок, вектор
і
мають
спільний початок, вектор
![]() іде
з кінця від’ємника в кінець зменшуваного.
іде
з кінця від’ємника в кінець зменшуваного.
