
- •Основні властивості (аксіоми) належності точок і прямих на площині
- •Висота, бісектриса, медіана трикутника
- •Дотична до кола
- •Геометричне місце точок
- •Пряма й обернена теореми
- •Доведеннявід супротивного
- •Приклади розв’язування типових задач з геометрії для 7 класу
- •Теорема Піфагора
- •Симетрія відносно прямої
- •Множення вектора на число
- •Скалярний добуток векторів
- •Подібність прямокутних трикутників
- •Пропорційність відрізків хорд і січних кола
- •Вписані й описані чотирикутники
- •Теорема синусів
- •Розв’язування трикутників
- •Многокутники
- •Правильні многокутники
- •Паралельність прямих і площини
- •Ознака паралельності площин
- •Перпендикулярність прямих і площин
- •Перпендикуляр і похила
- •Відстань між мимобіжними прямими
- •Кут між мимобіжними прямими
- •Декартові координати та вектори в просторі
- •Перетворення в просторі
- •Подібність просторових фігур
- •Вектори в просторі
- •Тригранний і многогранний кути
- •Паралелепіпед
- •Правильні многогранники
- •Описані кулі
Теорема Піфагора
Теорема
1 (Піфагора). У прямокутному трикутнику
квадрат гіпотенузи дорівнює сумі
квадратів катетів.
Правильною є і
теорема, обернена до теореми
Піфагора.
Теорема 2 (обернена). Коли
в трикутнику сторони a,
b,
c
і
![]() ,
то
цей трикутник є прямокутним з гіпотенузою
c.
Теорема
3. У прямокутному трикутнику будь-який
із катетів менший за гіпотенузу.
Корисно
пам’ятати довжину сторін деяких
прямокутних трикутників.
Єгипетський
трикутник: сторони дорівнюють 3, 4, 5
одиниць.
Тобто можливі варіанти: 3,
4, 5 або 6, 8, 10, або 3k,
4k,
5k,
де k
∈
N.
Також
прямокутними є трикутники зі сторонами,
які дорівнюють 5k,
12k,
13k;
8k,
15k,
17k;
7k,
24k,
25k,
де k
∈
N.
,
то
цей трикутник є прямокутним з гіпотенузою
c.
Теорема
3. У прямокутному трикутнику будь-який
із катетів менший за гіпотенузу.
Корисно
пам’ятати довжину сторін деяких
прямокутних трикутників.
Єгипетський
трикутник: сторони дорівнюють 3, 4, 5
одиниць.
Тобто можливі варіанти: 3,
4, 5 або 6, 8, 10, або 3k,
4k,
5k,
де k
∈
N.
Також
прямокутними є трикутники зі сторонами,
які дорівнюють 5k,
12k,
13k;
8k,
15k,
17k;
7k,
24k,
25k,
де k
∈
N.
Перпендикуляр і похила
Нехай
BA
— перпендикуляр,
опущений із точки B
на пряму a,
а С
— будь-яка точка прямої a,
відмінна від A
(див.
рисунок). Відрізок BC
називається похилою,
проведеною з точки B
до прямої a.
Точка С
називається основою
похилої.
Відрізок AС
називається проекцією
похилої.
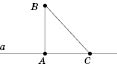
Властивості похилих
Теорема.
Коли з даної точки до прямої проведено
перпендикуляр і похилі, то будь-яка
похила більша від перпендикуляра; рівні
похилі мають рівні проекції, а з двох
похилих більша та, в якої проекція
більша.
На рисунку BD,
BC,
BP
— похилі, AB
— перпендикуляр,
![]() ;
;
![]() ;
;![]() .
.
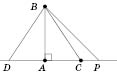
Нерівність трикутника
Теорема.
Які б не були три точки, відстань між
будь-якими двома із цих точок не більша,
ніж сума відстаней від них до третьої
точки.
Звідси випливає, що у будь-якому
трикутнику кожна сторона менша за суму
двох інших сторін, але більша за модуль
різниці двох інших сторін.
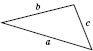 Якщо
a,
b
і c
— сторони трикутника (див. рисунок),
то
Якщо
a,
b
і c
— сторони трикутника (див. рисунок),
то
![]() ;
;
![]() ;
;
![]() .
.
Співвідношення між сторонами й кутом прямокутного трикутника
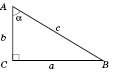
Нехай
ABC
—
прямокутний трикутник з прямим кутом
С
і гострим кутом при вершині A,
що дорівнює
![]() .
Косинусом
гострого кута прямокутного трикутника
називається відношення прилеглого
катета до гіпотенузи.
На рисунку
.
Косинусом
гострого кута прямокутного трикутника
називається відношення прилеглого
катета до гіпотенузи.
На рисунку
![]() або
або
![]() .
.
 Синусом
кута
називається
відношення протилежного катета до
гіпотенузи:
Синусом
кута
називається
відношення протилежного катета до
гіпотенузи:
![]() або
або
![]() .
Тангенсом
кута
називається
відношення протилежного катета до
прилеглого:
.
Тангенсом
кута
називається
відношення протилежного катета до
прилеглого:
![]() або
або
![]() .
Котангенсом
кута
називається
відношення прилеглого катета до
протилежного:
.
Котангенсом
кута
називається
відношення прилеглого катета до
протилежного:
![]() або
або
![]() .
Значення
.
Значення
![]() ,
,
![]() ,
,
![]() ,
,
![]() залежать
тільки від величини кута.
З означень
випливає, що для гострих кутів
і
залежать
тільки від величини кута.
З означень
випливає, що для гострих кутів
і
![]() прямокутного
трикутника (див. рисунок) маємо:
прямокутного
трикутника (див. рисунок) маємо:

![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
а також
,
а також
![]() ,
,
![]() .
Треба
вміти знаходити елементи прямокутного
трикутника, якщо дані яка-небудь сторона
й один із гострих кутів.
Розглянемо
такі задачі.
1. Дано:
.
Треба
вміти знаходити елементи прямокутного
трикутника, якщо дані яка-небудь сторона
й один із гострих кутів.
Розглянемо
такі задачі.
1. Дано:
![]() ;
;
![]() (гіпотенуза
і гострий кут).
Знайти: b;
a;
.
Розв’язання:
(гіпотенуза
і гострий кут).
Знайти: b;
a;
.
Розв’язання:
![]() ;
;
![]() ;
;
![]() .
2.
Дано:
.
2.
Дано:
![]() ;
;
![]() (катет
і прилеглий кут).
Знайти: a;
c;
.
Розв’язання:
;
(катет
і прилеглий кут).
Знайти: a;
c;
.
Розв’язання:
;
![]() ;
;
![]() .
3.
Дано:
.
3.
Дано:
![]() ;
;
![]() (катет
і протилежний кут).
Знайти: b;
c;
.
Розв’язання:
;
(катет
і протилежний кут).
Знайти: b;
c;
.
Розв’язання:
;
![]() ;
;
![]() .
Катет,
прилеглий до кута
,
дорівнює добутку гіпотенузи і
.
Катет,
протилежний куту
,
дорівнює добутку гіпотенузи і
.
Катет,
протилежний куту
,
дорівнює добутку другого катета і
.
Основні
тригонометричні тотожності, зміну
,
,
при
зростанні кута
описано
в розділі («Алгебра. 10 клас. Тригонометричні
функції»).
Значення
,
,
,
деяких
кутів:
.
Катет,
прилеглий до кута
,
дорівнює добутку гіпотенузи і
.
Катет,
протилежний куту
,
дорівнює добутку гіпотенузи і
.
Катет,
протилежний куту
,
дорівнює добутку другого катета і
.
Основні
тригонометричні тотожності, зміну
,
,
при
зростанні кута
описано
в розділі («Алгебра. 10 клас. Тригонометричні
функції»).
Значення
,
,
,
деяких
кутів:
 Корисним
є знання таких співвідношень.
1. Катет
прямокутного трикутника є середнім
пропорційним між гіпотенузою й проекцією
цього катета на гіпотенузу.
2. Висота
прямокутного трикутника, проведена з
вершини прямого кута, є середнім
пропорційним між проекціями катетів
на гіпотенузу.
На рисунку нижче в
трикутнику ABC:
Корисним
є знання таких співвідношень.
1. Катет
прямокутного трикутника є середнім
пропорційним між гіпотенузою й проекцією
цього катета на гіпотенузу.
2. Висота
прямокутного трикутника, проведена з
вершини прямого кута, є середнім
пропорційним між проекціями катетів
на гіпотенузу.
На рисунку нижче в
трикутнику ABC:
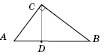
![]() ;
;
![]() ;
;
![]() .
.
Декартові координати на площині
Поняття декартових координат на площині описано в розділі «Математика, 6 клас».
Координати середини відрізка
Якщо
![]() ,
,
![]() —
довільні точки,
—
довільні точки,
![]() —
середина відрізка AB,
то
—
середина відрізка AB,
то
![]() ;
;
![]() .
.
Відстань між точками
Якщо
,
—
довільні точки і AB
відстань між ними, то
![]() або
або
![]() .
У
випадку, коли точка B
збігається з початком координат
.
У
випадку, коли точка B
збігається з початком координат
![]() ,
отримуємо:
,
отримуємо:
![]() .
Рівнянням
фігури на площині в декартових координатах
називається рівняння з двома змінними
x
і y,
яке задовольняють координати будь-якої
точки фігури й тільки вони.
.
Рівнянням
фігури на площині в декартових координатах
називається рівняння з двома змінними
x
і y,
яке задовольняють координати будь-якої
точки фігури й тільки вони.
Рівняння кола
![]() —
рівняння
кола з центром у точці
—
рівняння
кола з центром у точці
![]() і
радіусом R.
Зверніть
увагу:
рівняння
і
радіусом R.
Зверніть
увагу:
рівняння
![]() ,
де
,
де
![]() ,
задає коло й може бути зведеним до
стандартного виду.
,
задає коло й може бути зведеним до
стандартного виду.
Рівняння прямої
Будь-яка
пряма в декартових координатах x,
y
має рівняння виду:
![]() ,
де a,
b,
c
— деякі числа.
Знаходження координат
точки перетину прямих та випадки
розміщення прямої відносно системи
координат описано в розділі «Алгебра.
8 клас» («Лінійна функція»).
Рівняння
прямої, яка перетинає осі координат в
точках
,
де a,
b,
c
— деякі числа.
Знаходження координат
точки перетину прямих та випадки
розміщення прямої відносно системи
координат описано в розділі «Алгебра.
8 клас» («Лінійна функція»).
Рівняння
прямої, яка перетинає осі координат в
точках
![]() і
і
![]() ,
де
,
де
![]() ,
,
![]() ,
можна записати у вигляді:
,
можна записати у вигляді:
![]() .
.
Кутовий коефіцієнт у рівнянні прямої
Якщо
рівняння прямої можна записати у
вигляді![]() ,
то коефіцієнт
k називається
кутовим
коефіцієнтом прямої.
1.
Дві прямі паралельні тоді й тільки тоді,
коли у них збігаються кутові коефіцієнти,
а точки перетину з віссю ординат різні.
2.
Кутовий коефіцієнт з точністю до знака
дорівнює тангенсу гострого кута,
утвореного прямою з віссю абсцис (або
дорівнює тангенсу кута між прямою й
додатним напрямком осі Ox).
3.
Прямі, що задані рівняннями
,
то коефіцієнт
k називається
кутовим
коефіцієнтом прямої.
1.
Дві прямі паралельні тоді й тільки тоді,
коли у них збігаються кутові коефіцієнти,
а точки перетину з віссю ординат різні.
2.
Кутовий коефіцієнт з точністю до знака
дорівнює тангенсу гострого кута,
утвореного прямою з віссю абсцис (або
дорівнює тангенсу кута між прямою й
додатним напрямком осі Ox).
3.
Прямі, що задані рівняннями
![]() і
і![]() ,
перпендикулярні тоді й тільки тоді,
коли
,
перпендикулярні тоді й тільки тоді,
коли
![]() .
.
Означення синуса, косинуса, тангенса, котангенса для будьякого кута від 0° до 180°
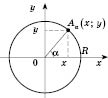
Візьмемо
коло на площині
Oxy
з центром у початку координат і радіусом
R.
Відкладемо
від додатної півосі Ox
кут
у
верхню півплощину (див. рисунок нижче).
Точку перетину сторони кута з колом
назвемо
![]() .
Вона має координати
.
Вона має координати
![]() .
Тоді
.
Тоді
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
 При
такому означенні:
При
такому означенні:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() не
існує;
не
існує;
![]() ;
;
![]() ;
;
![]() не
існує.
не
існує.
![]() ;
;
![]() ;
;
![]()
![]() .
.
Рух
Якщо кожну точку даної фігури змістити деяким чином, то дістанемо нову фігуру. Кажуть, що ця фігура утворюється перетворенням даної. Перетворення однієї фігури в іншу називається рухом, якщо це перетворення зберігає відстань між точками.
Властивості руху
1. Два рухи, виконані послідовно, дають знову рух. 2. Перетворення, обернене до руху, є рух. 3. Під час руху точки, що лежать на прямій, переходять у точки, які лежать на прямій, і зберігається порядок їх взаємного розміщення. 4. Під час руху прямі переходять у прямі, півпрямі — у півпрямі, відрізки — у відрізки. 5. Під час руху зберігаються кути між півпрямими. 6. Під час руху паралельні прямі переходять у паралельні прямі.
Симетрія відносно точки
Нехай
O
— фіксована точка, X
—
довільна точка площини. Відкладемо на
продовженні відрізка OX
за точку O
відрізок
![]() ,
що дорівнює OX.
Точка
,
що дорівнює OX.
Точка
![]() називається
симетричною
точці X
відносно точки O(див.
рисунок).
називається
симетричною
точці X
відносно точки O(див.
рисунок).
![]() Очевидно,
що точка, симетрична
,
є точка X.
Перетворення
фігури F
у
фігуру
Очевидно,
що точка, симетрична
,
є точка X.
Перетворення
фігури F
у
фігуру
![]() ,
при якому кожна її точка X
фігури F
переходить
у точку
,
симетричну відносно точки O,
називається перетворенням
симетрії відносно точкиO.
Фігури
F
і
називаються
симетричними
відносно точкиO
(див. рисунок).
,
при якому кожна її точка X
фігури F
переходить
у точку
,
симетричну відносно точки O,
називається перетворенням
симетрії відносно точкиO.
Фігури
F
і
називаються
симетричними
відносно точкиO
(див. рисунок).
 Якщо
перетворення симетрії відносно точки
O
переводить фігуру F
у себе, то фігура F
називається центрально-симетричною,
а точка O
— її центром
симетрії.
Наприклад, точка перетину діагоналей
паралелограма є його центром симетрії
(рисунок нижче зліва). Центр кола є його
центром симетрії (рисунок справа).
Якщо
перетворення симетрії відносно точки
O
переводить фігуру F
у себе, то фігура F
називається центрально-симетричною,
а точка O
— її центром
симетрії.
Наприклад, точка перетину діагоналей
паралелограма є його центром симетрії
(рисунок нижче зліва). Центр кола є його
центром симетрії (рисунок справа).
 Теорема.
Перетворення симетрії відносно точки
є рухом.
Теорема.
Перетворення симетрії відносно точки
є рухом.
