Паралельність прямих і площини

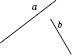
Дві прямі в просторі називаються паралельними, якщо вони лежать в одній площині й не перетинаються. Прямі, які не лежать в одній площині, називаються мимобіж­ними. Зверніть увагу: «не лежать в одній площині» і «лежать у різних площинах» — це різні твердження. Наприклад, паралельні прямі a і b лежать у різних площинах і (див. рисунок), але через них можна провести площину, яка міститиме a і b водночас. Для мимобіжних прямих (див. рисунок) не існує такої площини, у якій вони лежали б водночас. Можна довести, що всі прямі, які перетинають дві паралельні прямі, лежать в одній площині. Теорема. Через точку, яка не лежить на даній прямій, можна провести пряму, паралельну даній, і тільки одну.

Ознака паралельності прямих

Теорема. Дві прямі, паралельні третій прямій, паралельні між собою. Із цієї теореми випливає, що середини сторін просторового чотирикутника (див. рисунок) є вершинами паралелограма (вершини просторового чотирикутника не лежать в одній площині). 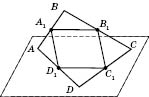Зверніть увагу: якщо ABCD — просторовий чотирикутник, то його діагоналі AC і BD — мимобіжні прямі.

Ознака паралельності прямої і площини

Теорема 1. Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині. Теорема 2. Якщо пряма паралельна площині, то на цій площині знайдеться пряма, яка паралельна даній прямій. Зверніть увагу: паралельність прямої і площини не означає, що ця пряма паралельна будь-якій прямій на цій площині. Кожна пряма цієї площини буде або паралельна даній, або мимобіжна з нею. На рисунку: ; ; ; a і b — мимобіжні; . Теорема 3. Через точку, що не лежить на площині, можна провести безліч прямих, паралельних даній площині, причому всі вони лежать в одній площині (паралельній даній). Теорема 4. Якщо площина перетинає одну з двох паралельних прямих, то вона перетинає й другу пряму (див. рисунок). На рисунку . Дві площини називаються паралельними, якщо вони не перетинаються.

Ознака паралельності площин

Теорема 1. Якщо дві прямі однієї площини, які перетинаються й відповідно паралельні двом прямим другої площини (див. рисунок), то ці площини паралельні. Теорема 2 (обернена). Якщо в одній площині є дві прямі, які перетинаються, і ці прямі паралельні другій площині, то такі площини паралельні. Зверніть увагу: прямі мають обов’язково перетинатися. Дійсно, в площині може бути скільки завгодно прямих, паралельних прямій a (див. рисунок нижче), а значить, і площині , і при цьому площини і не будуть паралельними. Теорема 3. Якщо пряма перетинає одну з двох паралельних площин, то вона перетинає й другу (див. рисунок). Теорема 4. Через дві мимобіжні прямі можна провести паралельні площини (рисунок нижче ­зліва). Теорема 5. Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну (рисунки нижче). Теорема 6. Якщо дві площини паралельні третій, то вони паралельні одна одній.

Властивості паралельних площин

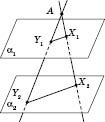Теорема 1. Якщо дві паралельні площини перетинаються третьою площиною (див. рисунок), то прямі перетину паралельні. На рисунку: ; . Теорема 2. Відрізки паралельних прямих, які містяться між двома паралельними площинами (див. рисунок), рівні. На рисунку: ; ; . Теорема 3. Нехай площини і паралельні (див. рисунок нижче) і є точка A, яка не лежить у жодній із цих площин. Через точку A проведено довільну пряму. Нехай і — точки перетину прямої з площинами і . Відношення довжини відрізків не залежить від узятої прямої (AY1 : AY2 = AX1 : AX2).

Зображення просторових фігур на площині

Для зображення просторових фігур на площині, як правило, користуються паралельним проектуванням. Беремо довільну пряму h, яка перетинає площину рисунка , проводимо через довільну точку A фігури пряму, паралельну h. Точка перетину цієї прямої з площиною рисунка буде зображенням точки A. Побудувавши таким чином зображення кожної точки фігури, дістанемо зображення самої фігури. Такий спосіб зображення фігури на площині і є паралельне проектування. У випадку, коли пряма h перпендикулярна до площини , кажуть, що проведено ортогональне проектування.

Властивості паралельного проектування

1. Прямолінійні відрізки фігури зображуються на площині рисунка відрізками або точками. (Якщо відрізок, що проектується, паралельний напрямку проектування, він проектується в точку.) 2. Паралельні відрізки фігури зображуються на площині рисунка паралельними відрізками. 3. Відношення відрізків однієї прямої або паралельних прямих зберігається при паралельному проектуванні. Зверніть увагу: при паралельному проектуванні не зберігаються ані довжина відрізка, ані величина кута. Із властивостей паралельного проектування випливають такі твердження. 1. Будь-який трикутник може бути зображений довільним трикутником. 2. Якщо проектується у , то медіани проектуються в медіани, середні лінії — у середні лінії, а висоти й бісектриси не проектуються у висоти й бісектриси. Проте основа проекції бісектриси поділяє сторону проекції трикутника у тому ж відношенні, що основа бісектриси поділяє сторону трикутника. 3. Паралелограм зображується паралелограмом. Прямокутник, квадрат, ромб — паралелограмом загального виду. 4. Трапеція зображується трапецією. Рівно­біч­ність або прямокутність не зберіга­ється. Зверніть увагу, як побудувати зображення висот рівнобічної трапеції: на рисунку — зобра­ження трапеції, отримане при паралельному проектуванні. 1) Будуємо . 2) Будуємо точку — середину . 3) — висота . 4) . Отже, B1P1 і — зображення висот рівнобічної трапеції ABCD, проекцією якої є трапеція . 5. Коло зображується еліпсом. 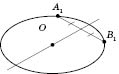Якщо — проекція хорди AB (див. рисунок), то, щоб побудувати зображення діаметра, перпендикулярного до AB, досить провести пряму через центр О і середину . (Діаметр, перпендикулярний до хорди, проходить через її середину.)